Презентація на тему:
Італійське відродження

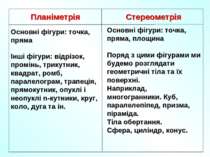
Планіметрія Стереометрія Вивчає властивості геометричних фігур на площині Вивчає властивості фігур у просторі В перекладі з грецької слово «геометрія» означає «землемірство» «гео» – на грецькій земля, «метрео» – міряти Слово «стереометрія» походить від грецьких слів «стереос» об’ємний, простірний, «метрео» – міряти

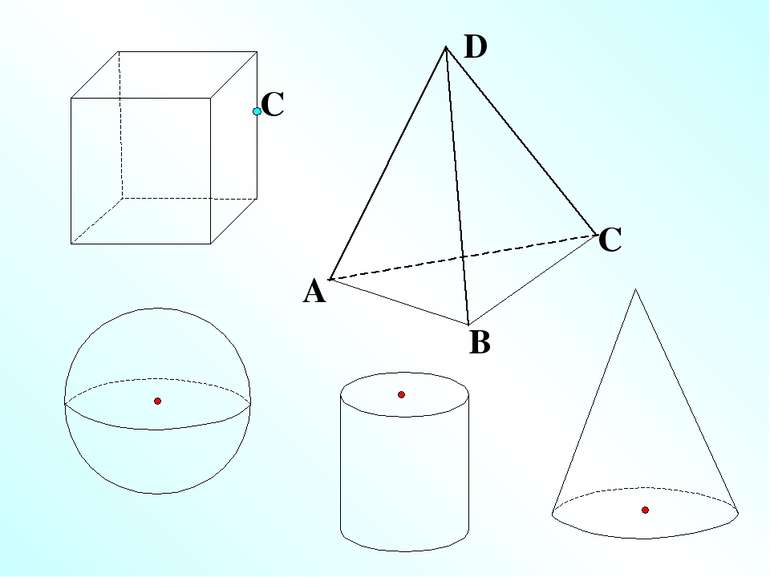
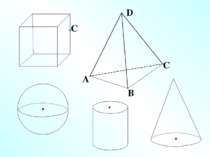
Планіметрія Стереометрія Поряд з цими фігурами ми будемо розглядати геометричні тіла та їх поверхні. Наприклад, многогранники. Куб, паралелепіпед, призма, піраміда. Тіла обертання. Сфера, циліндр, конус. Основні фігури: точка, пряма Основні фігури: точка, пряма, площина Інші фігури: відрізок, промінь, трикутник, квадрат, ромб, паралелограм, трапеція, прямокутник, опуклі і неопуклі n-кутники, круг, коло, дуга та ін.

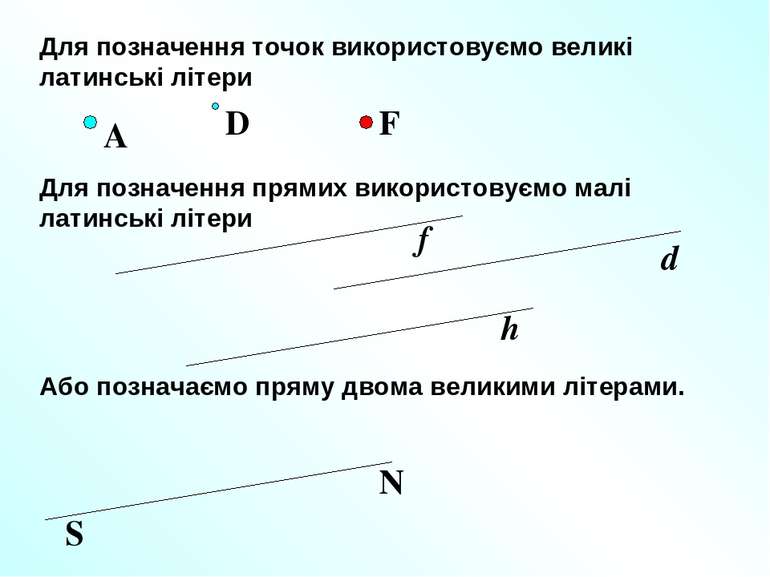
Для позначення точок використовуємо великі латинські літери Для позначення прямих використовуємо малі латинські літери Або позначаємо пряму двома великими літерами.

Площини будемо позначати малими грецькими літерами. На рисунках площини зображуються паралелограмами. Площину слід уявляти собі як нескінченну поверхню, яка простягається у всі сторони.

C

Стереометрія широко використовується в будівництві, архітектурі, машинобудуванні, в інших областях науки і техніки. При проектуванні цієї машини важливо було отримати таку форму, щоб при русі опір повітря був мінімальний.

Оперний театр в Сіднеї

Ейфелева вежа Париж, Марсове поле Інженер Гюстав Ейфель знайшов незвичну форму для свого проекту. Ейфелева вежа досить стійка: сильний вітер схиляє її вершину всього лише на 10-12 см. В спеку від нерівномірного нагрівання сонячними променями вона може відхилитися на 18 см.

18000 залізних деталей скріпляються 2500000 защібок

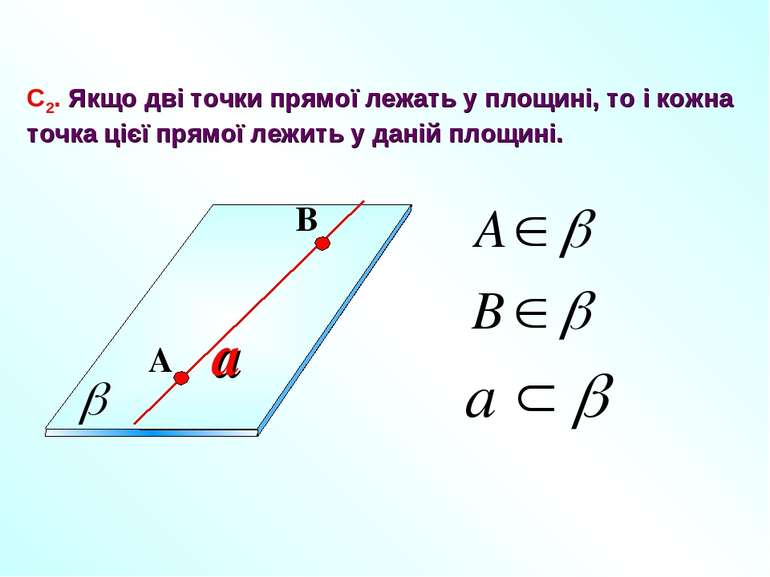
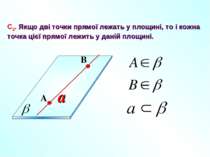
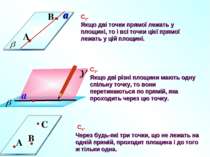
a С2. Якщо дві точки прямої лежать у площині, то і кожна точка цієї прямої лежить у даній площині. A B

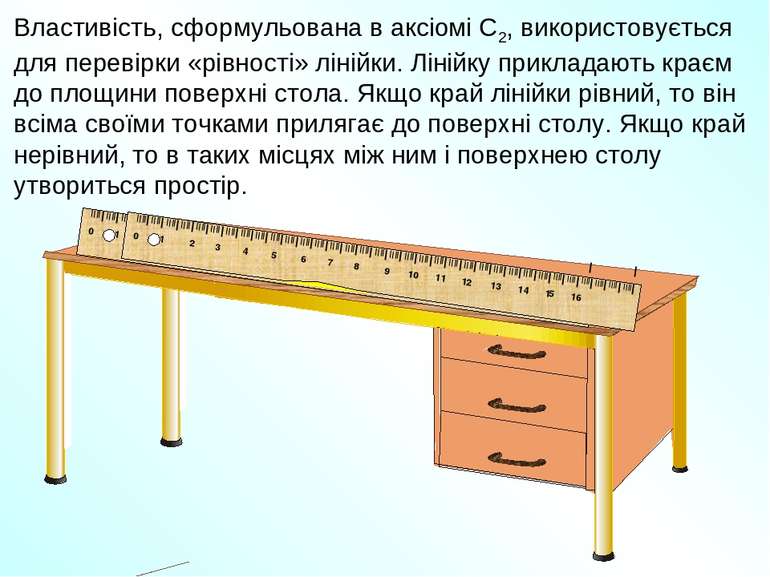
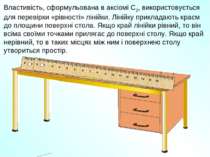
Властивість, сформульована в аксіомі С2, використовується для перевірки «рівності» лінійки. Лінійку прикладають краєм до площини поверхні стола. Якщо край лінійки рівний, то він всіма своїми точками прилягає до поверхні столу. Якщо край нерівний, то в таких місцях між ним і поверхнею столу утвориться простір.

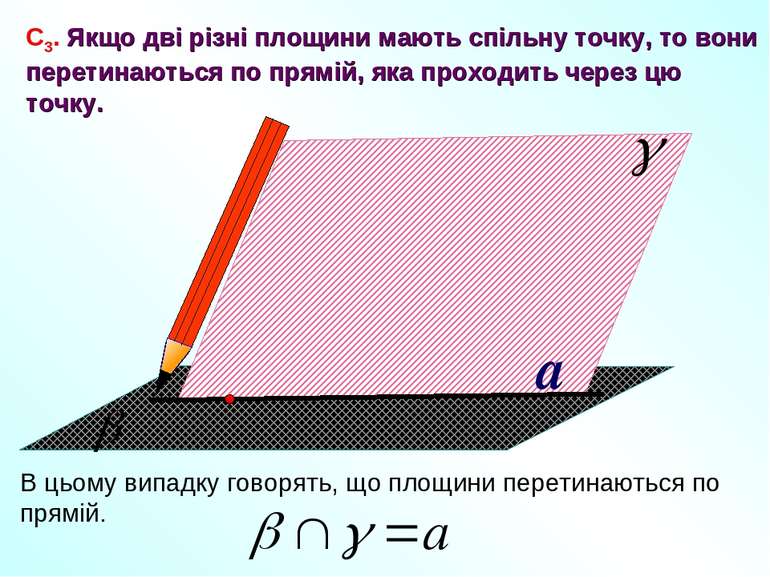
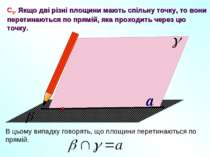
a С3. Якщо дві різні площини мають спільну точку, то вони перетинаються по прямій, яка проходить через цю точку. В цьому випадку говорять, що площини перетинаються по прямій.

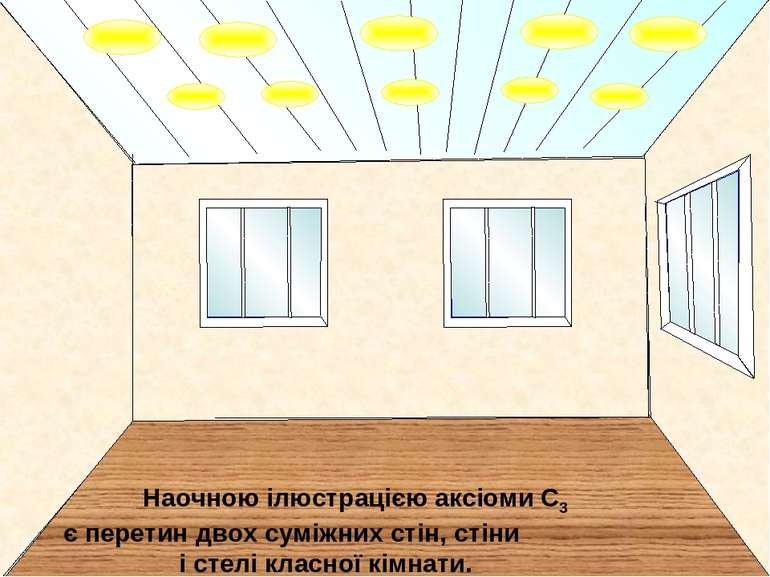
Наочною ілюстрацією аксіоми С3 є перетин двох суміжних стін, стіни і стелі класної кімнати.

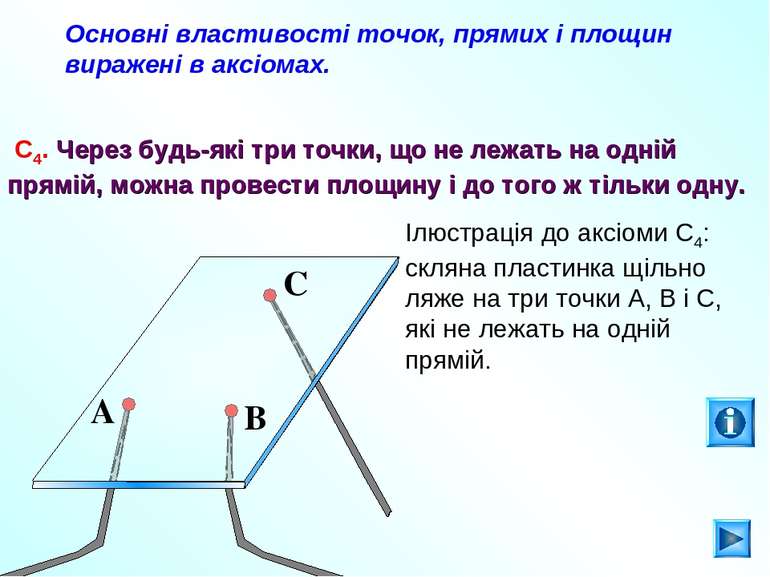
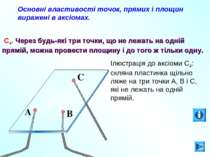
Основні властивості точок, прямих і площин виражені в аксіомах. С4. Через будь-які три точки, що не лежать на одній прямій, можна провести площину і до того ж тільки одну. Ілюстрація до аксіоми С4: скляна пластинка щільно ляже на три точки А, В і С, які не лежать на одній прямій. A B C

Ілюстрації до аксіоми С4 із життя. Табуретка із трьома ніжками завжди ідеально стане на підлогу і не буде гойдатися. У табуретки з чотирма ніжками бувають проблеми зі стійкістю, якщо ніжки стільця не однакової довжини. Табуретка розкачується, тобто опирається на три ніжки, а четверта ніжка (четверта «точка») не лежить в площині підлоги, а висить в повітрі. Для відеокамери, фотозьомки і для інших пристроїв часто використовують штатив – треногу. Три ніжки штатива стійко розміщуються на будь-якій підлозі в приміщеннях, на асфальті або прямо на газоні на вулиці, на піску на пляжі або в траві в лісі. Три ніжки штатива завжди знайдуть площину.

С4. Через будь-які три точки, що не лежать на одній прямій, проходит площина і до того ж тільки одна.

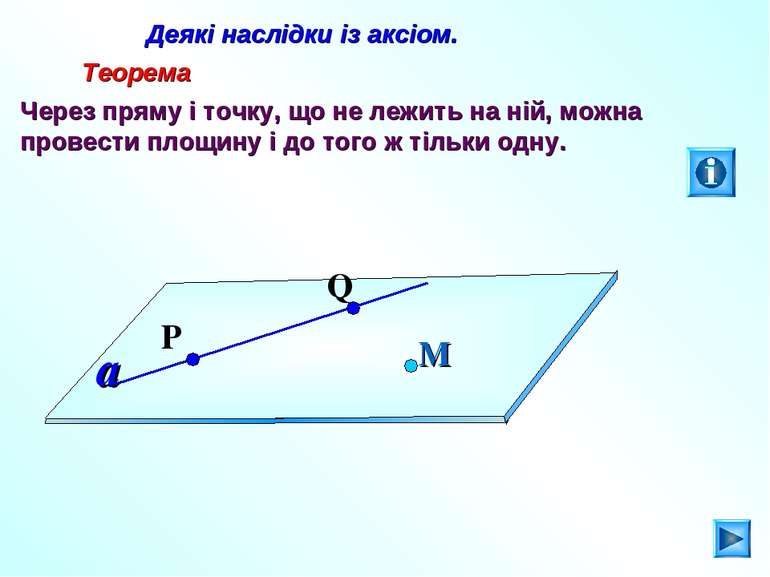
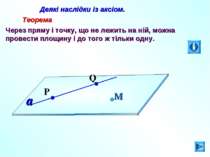
Деякі наслідки із аксіом. Теорема Через пряму і точку, що не лежить на ній, можна провести площину і до того ж тільки одну. М a

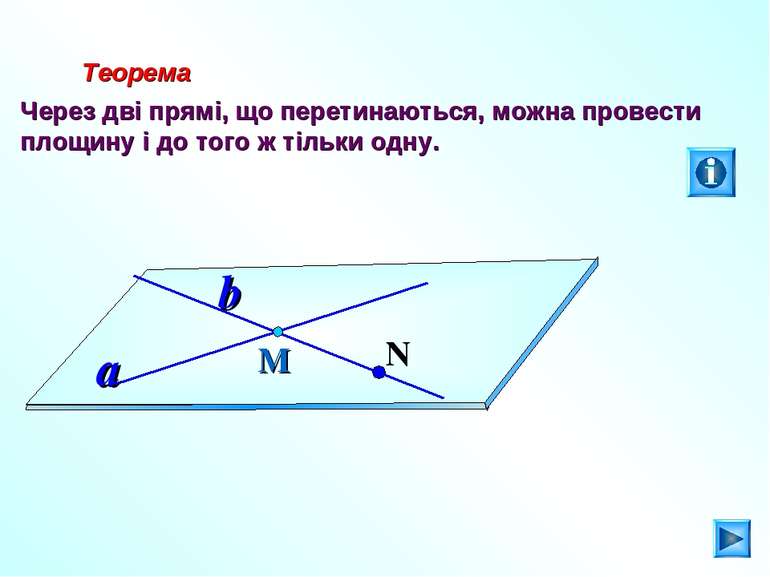
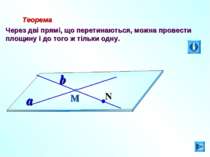
Теорема Через дві прямі, що перетинаються, можна провести площину і до того ж тільки одну. М a b N

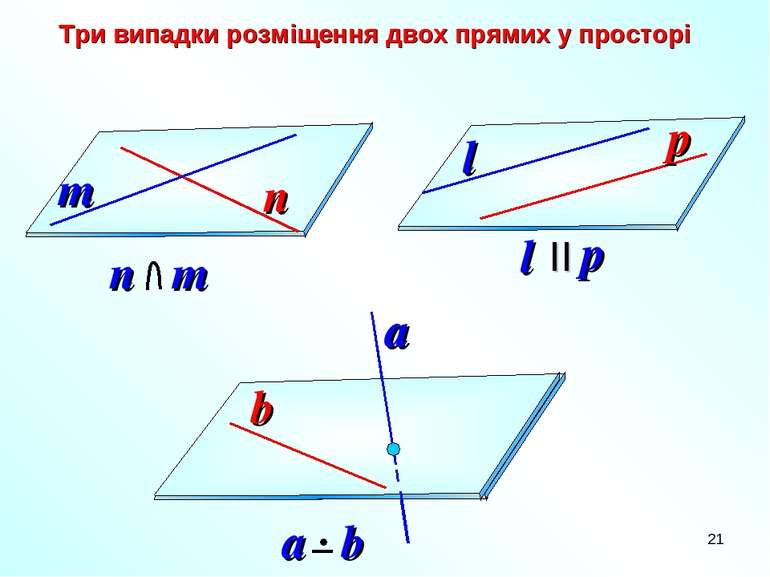
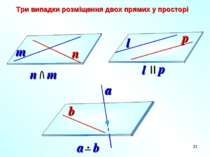
Трьома точками, які не лежать на одній прямій. Прямою і точкою, яка не лежить на ній. Двома прямими, що перетинаються. . . . . A B C a A a b .

* Три випадки розміщення двох прямих у просторі

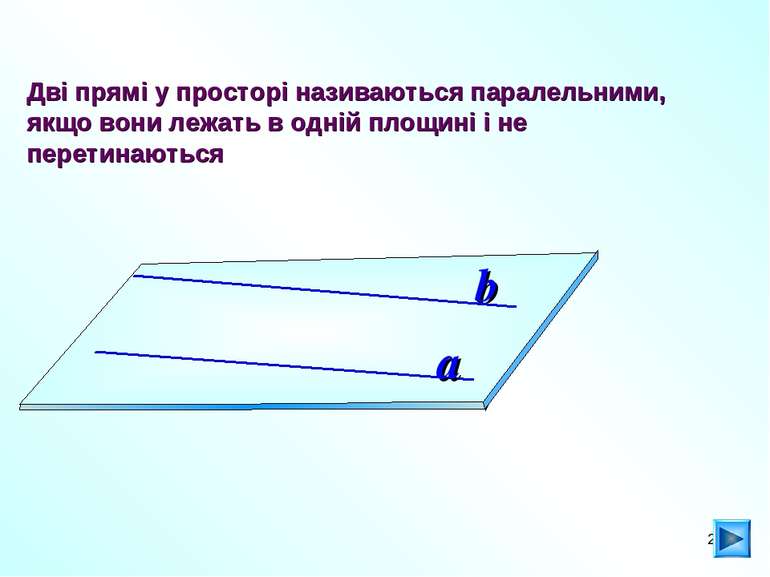
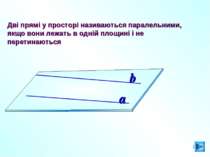
* Дві прямі у просторі називаються паралельними, якщо вони лежать в одній площині і не перетинаються a b

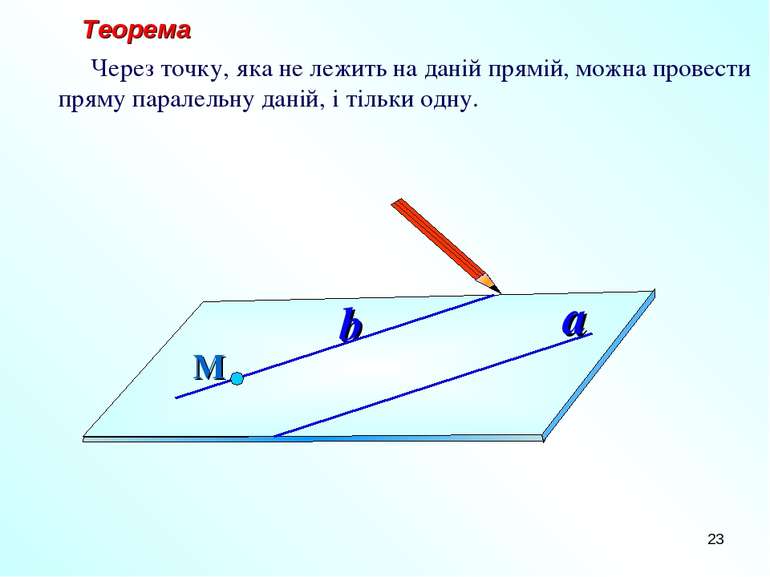
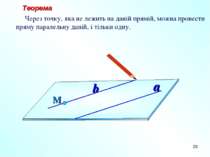
* Теорема Через точку, яка не лежить на даній прямій, можна провести пряму паралельну даній, і тільки одну. М a b

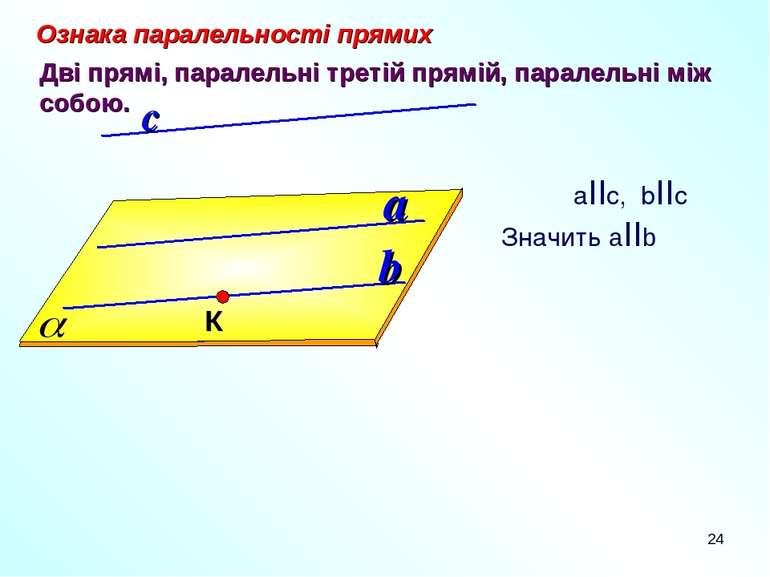
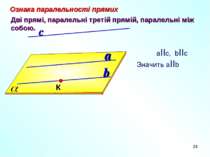
* a b с Ознака паралельності прямих Дві прямі, паралельні третій прямій, паралельні між собою. aIIс, bIIс Значить aIIb

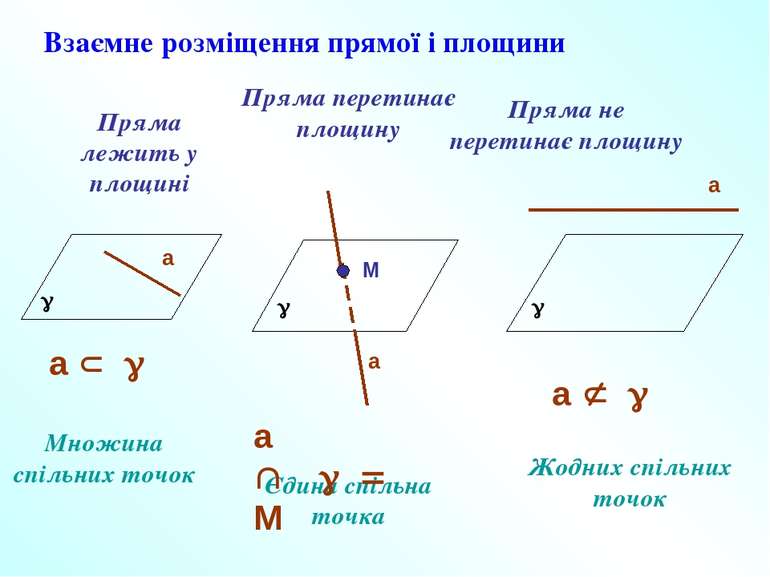
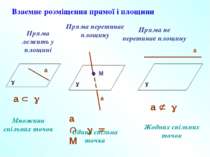
Взаємне розміщення прямої і площини Пряма лежить у площині Пряма перетинає площину Пряма не перетинає площину Множина спільних точок Єдина спільна точка Жодних спільних точок g а g а М g а а Ì g а Ç g = М а Ë g

a b Ознака паралельності прямої і площини Якщо пряма, яка не належить площині, паралельна якій-небудь прямій в цій площині, то вона паралельна і самій площині.