Презентація на тему:
ТЕОРЕТИЧНІ ОСНОВИ МЕТРОЛОГІЧНОГО ЗАБЕЗПЕЧЕННЯ

* Дисципліна: “ТЕОРЕТИЧНІ ОСНОВИ МЕТРОЛОГІЇ” Тема № 2. ТЕОРЕТИЧНІ ОСНОВИ МЕТРОЛОГІЧНОГО ЗАБЕЗПЕЧЕННЯ Заняття № 5 Визначення числових характеристик випадкових величин Навчальна мета: 1.Вивчити елементи математичної статистики; оцінки, точечні і інтервальні оцінки. 2.Вивчити властивості елементів математичної статистики. 3.Розглянути поняття про помилки першого та другого роду. Доцент кафедри , к.т.н. Лях М.А. КАФЕДРА ВІЙСЬКОВОГО УПРАВЛІННЯ

Навчальні питання Вступ……………………………. 10 хв. 2. Основна частина……………….65 хв. 1.Оцінки. Властивості оцінок. Точечні і інтервальні оцінки.....................30 хв. 2.Принцип практичної упевненості…………………….. 15 хв. 3.Поняття про помилки першого і другого роду……….……..........................20 хв. Заключна частина……………........ 5 хв.

Всі дослідження випадкових явищ, які виконані методом ймовірності, прямо або непрямо спираються на експериментальні дані. Обробка статистичних з метою одержання найбільш точного наближеного значення величини, яка підлягає дослідженню, складає предмет математичної статистики. Математична статистика вивчає математичні методи систематизації і обробки результатів спостережень масових випадкових явищ з метою одержання необхідних для практики даних. Нехай в результаті n спостережень величини а одержаний ряд можливих значень Х1,Х2,...,Хі,...,Хn (1) Ряд (1) це вибірка n, відібрана навмання з генеральної сукупності; n елементів вибірки створюють емпіричний розподіл. Шляхом обробки елементів вибірки можна обчислити статистичні характеристики емпіричного розподілу. В силу випадковості вибірки і обмеженості її об єму статистичні характеристики є випадковими величинами і відрізняються від числових характеристик теоретичного розподілу, якому підлягає генеральна сукупність. Тому числові значення статистичних характеристик можуть бути визначені тільки приблизно. 1. ОЦІНКИ. ВЛАСТИВОСТІ ОЦІНОК. ТОЧЕЧНІ І ІНТЕРВАЛЬНІ ОЦІНКИ.

Точечні оцінки Визначення: Приблизне значення оцінюваної величини (а) , яке приймається замість істинного значення цієї величини а, називається оцінкою . Оцінку прийнято позначати тією ж самою літерою, що і оцінювану величину, але з хвилястою рискою над нею. Так як оцінка (а )обчислюється по елементах вибірки (1) то оцінка є функцією величини Х1,Х2,...,Хі,...,Хn. Тобто, сама оцінка є випадковою величиною. Для повної характеристики необхідно знати закон її розподілу. Деякі поняття про якість оцінки можна одержати, якщо досліджувати її властивості, які визначають здатність оцінки для описання самої випадкової величини. Найбільш важливими з цих властивостей є: а) спроможність (состоятельность – рос.); б) ефективність.

1.Оцінка параметра (а) називається спроможною, якщо при збільшенні об єму вибірки / п/ вона сходиться за ймовірністю до очікуваного параметра а, т.б.т. якщо при будь-якому >0 виконується умова (2) Розглянемо декілька визначень пов’язаних з оцінками. 2.Дисперсія спроможної оцінки при n прямує до нуля. Спроможну оцінку можна прийняти за приблизне значення параметра, але при умові, що / n/ велике. 3.Оцінка називається незміщеною, якщо математичне сподівання оцінки дорівнює очікуваному параметру незалежно від числа спостережень, т.б.т., якщо при будь-якому / n/ виконується умова : M[ ]= a (3) 4.Якщо рівність (3) виконується при n , то оцінку називають асимптотично незміщеною. 5.Якщо існує ряд незміщених оцінок, то найкращою рахують ту у якої найменша дисперсія. Незміщена оцінка, яка має найменшу дисперсію, називається ефективною: D[ ]= min (4) 6.Якщо умова (4) виконується при n , то оцінка називається асимптотично ефективною.

7.Середнє арифметичне : - є спроможною і незміщеною оцінкою математичного сподівання. Якщо випадкова величина Х підлягає нормальному закону, то Х є також ефективною оцінкою. . (6) (5) є спроможною і незміщеною, але не ефективною. Якщо випадкова величина Х розподілена згідно з нормальним законом, то оцінка дисперсії є асимптотично ефективною. Оцінка дисперсії:

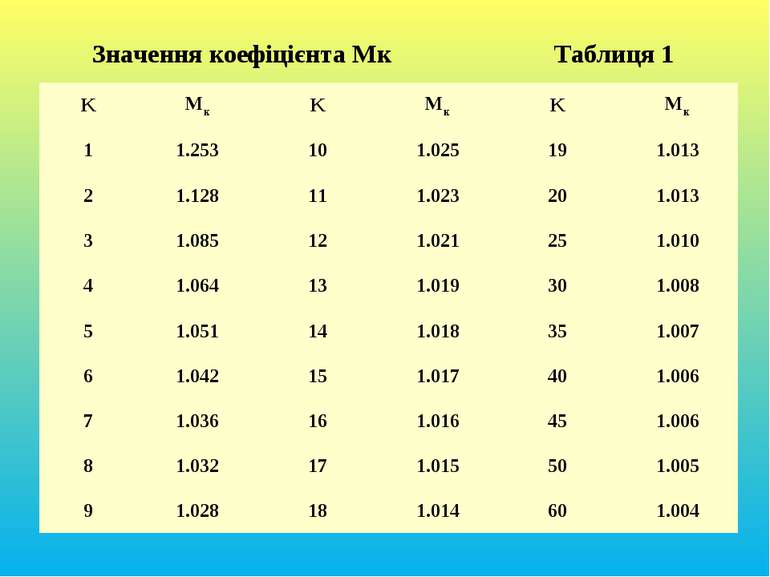
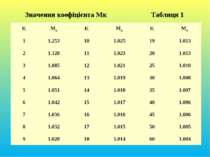
Якщо оцінка дисперсії спроможна, то і оцінка середнього квадратичного відхилення є спроможною. Однак, оскільки співвідношення між і нелінійне, то оцінка Для усунення зміщення оцінки середнього квадратичного відхилення нормально розподіленої величини необхідно ввести коректуючий множник (див. таблицю 1). де к = n –1 (7) В цьому випадку незміщена оцінка середнього квадратичного відхилення S визначається виразом : (8) не є незміщеною, а буде асимптотично незміщеною оцінкою.

Значення коефіцієнта Мк Таблиця 1 K Mк K Mк K Mк 1 1.253 10 1.025 19 1.013 2 1.128 11 1.023 20 1.013 3 1.085 12 1.021 25 1.010 4 1.064 13 1.019 30 1.008 5 1.051 14 1.018 35 1.007 6 1.042 15 1.017 40 1.006 7 1.036 16 1.016 45 1.006 8 1.032 17 1.015 50 1.005 9 1.028 18 1.014 60 1.004

Розглянуті вище оцінки - приблизне значення, - оцінка середньоквадратичного відхилення, - середнє арифметичне, які виражаються деяким числом (точкою на числовій осі), прийнято називати точечними. Оскільки вибірка є випадковою, особливо при малих об ємах / n/, така оцінка може опинитись далекою від істинного значення параметра. , ,

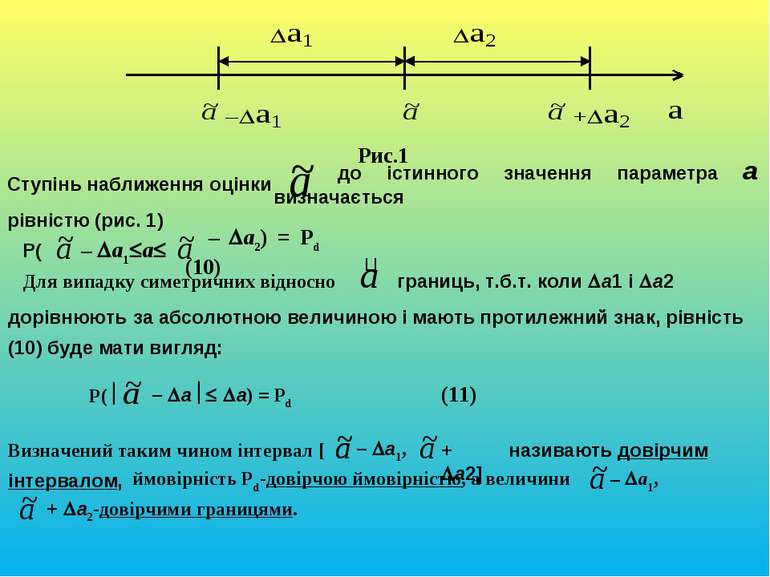
Інтервальні оцінки . Вичерпуючою характеристикою ступеню наближення оцінки(а) до параметра а, т.б.т. точністю оцінки, є її закон розподілу. Однак така характеристика точності складна в її використанні. Тому в математичній статистиці для характеристики точності оцінки використовується інтервальна оцінка, яка визначається двома числами – границями інтервалу рис.1 [ – a1, + a2] (9) в границях якого з певною ймовірністю знаходиться істинне значення оцінюваного параметра .

Рис.1 Ступінь наближення оцінки до істинного значення параметра a визначається – a1 a – a2) = Pd (10) P( – a a) = Pd (11) рівністю (рис. 1) P( Для випадку симетричних відносно границь, т.б.т. коли a1 і a2 дорівнюють за абсолютною величиною і мають протилежний знак, рівність (10) буде мати вигляд: Визначений таким чином інтервал [ – a1, ймовірність Pd-довірчою ймовірністю, а величини – a1, + a2-довірчими границями. + a2] називають довірчим інтервалом,

Слід відмітити, що близькість довірчої ймовірності до одиниці ще не гарантує (в ймовірнісному розумінні) близькість оцінки(а) до параметра a, якщо даному значенню Pd відповідає широкий довірчий інтервал. Вузький довірчий інтервал сам по собі також не характеризує якість оцінки (а) , якщо йому не відповідає висока довірча ймовірність. Таким чином, довірчу ймовірність і довірчий інтервал необхідно завжди розглядати в сукупності. За допомогою виразів (10) і (11) можна знайти довірчий інтервал при заданій довірчий ймовірності або визначити довірчу ймовірність при заданому довірчому інтервалі. В більшості прикладних задач метрології визначається довірчий інтервал по заданій довірчій ймовірності.

Згідно з міждержавним стандартом ГОСТ 8.207-76 (ГСИ. Прямые измерения с многократными повторениями. Методы обработки результатов наблюдений. Основные положения.), довірчу ймовірність Pd для визначення довірчих границь похибки результату вимірювання приймають рівною 0.95. В таких випадках коли вимірювання не можна повторити, крім довірчих границь, які відповідають довірчій ймовірності Pd = 0.95, допускається вказувати границі для довірчої ймовірності Pd = 0.99. Згідно з міждержавним стандартом ГОСТ 8.381-80 (Прим.1) довірчу ймовірність при визначенні довірчих границь похибки еталона приймають рівною 0.99. Висновок: Таким чином вище розглянуті оцінки, властивості оцінок, точечні і інтервальні оцінки, довірчі ймовірності, довірчі інтервали, а також зв’язок останніх при вирішенні прикладних задач метрології.

2.ПРИНЦИП ПРАКТИЧНОЇ ВПЕВНЕНОСТІ. ПРИНЦИП ЗНАЧИМОСТІ. Оцінки будь-якого параметра генеральної сукупності внаслідок обмеженого об’єму вибірки є випадковими величинами. Однак на основі цих оцінок повинні надаватись практичні рекомендації. Наприклад на основі групи спостережень вказують певний результат вимірювання, хоча ймовірність того, що цей результат дорівнює дійсному значенню, завжди менша одиниці. Якщо при цьому оцінюється похибка вимірювання то і вона може бути знайдена з певним ступенем точності. На практиці рахується, що похибка вимірювання значно менша результату вимірювання. В свою чергу із теорії ймовірностей слідує, що похибка може бути як завгодно великою (хоча ймовірність появи такої похибки дуже мала). Протиріччя, яке виникає між теорією і практикою можна вирішити, якщо замість неможливих і достовірних подій використовувати так звані практично достовірні і неможливі події, ймовірність появи яких близькі відповідно одиниці і нулю.

Наприклад, якщо відомо, що ймовірність появи події А в даному досліді дорівнює 0.3, то це ще не дає можливості передбачити результат досліду. Але якщо ймовірність події А в даному досліді мізерно мала, або навпаки, надто близька до одиниці то це вже дає можливість передбачати результат досліду з достатньою підставою. При цьому керуються принципом практичної впевненості, який формулюється наступним чином. Якщо ймовірність деякої події в даному досліді дуже мала (велика), то можна бути практично впевненим в тому що при одноразовому виконанні досліду подія А не здійсниться (здійсниться). Іншими словами події з дуже малими (великими) ймовірностями можна вважати практично неможливими (достовірними). Природно виникає питання: наскільки малою повинна бути ймовірність події, щоб можна було рахувати неможливим її появу в одному випробуванні. Найбільше значення малої ймовірності, при якій подію можна рахувати практично неможливою, називають рівнем значимості.

Питання про кількісне значення рівня значимості виходить за рамки математичної теорії, і в кожному конкретному випадку воно вирішується з практичних міркувань в залежності від того, наскільки важливе значення має прийняте рішення і наскільки велика небезпека одиночної помилки. На практиці як правило приймають рівень значимості 0,05; 0,02; 0,01 і рідше 0,1 або 0,2. Згідно з міждержавним стандартом ГОСТ 8.207-76, при перевірці гіпотези про те, що результати спостережень належать нормальному розподілу, приймають рівні значимості від 0,1 до 0,02. Висновок : Т.ч. в даному питанні розглянуті поняття принципу практичної впевненості і рівня значимості і як вони застосовуються на практиці.

3.КРИТЕРІЇ ЗГОДИ. ПОНЯТТЯ ПРО ПОМИЛКИ ПЕРШОГО І ДРУГОГО РОДУ. Критерії згоди. При вивченні закону розподілу випадкової величини на основі даних статистичного матеріалу висувається гіпотеза про теоретичний розподіл. Між статистичним і теоретичним розподілами завжди має місце деяке розходження, яке обумовлене випадковими обставинами, які зв’язані або з поганим узгодженням розподілів, або з обмеженим об’ємом вибірки. Основна вимога до теоретичного розподілу полягає в тому, щоб воно відображало б лише суттєві сторони статистичного матеріалу, а не випадкові, які обумовлені недостатніми експериментальними даними. Ступінь узгодженості між теоретичними і практичними розподілами може бути оцінена за допомогою критерію згоди. Критерієм згоди називають критерій перевірки гіпотези про передбачуваний закон невідомого розподілу.

Вибирається деяка величина , яка характеризує ступінь розходження теоретичного і статистичного розподілів. Вона може бути вибрана різними способами. Величина повинна задовольняти деяким загальним вимогам. Необхідно, щоб закон розподілу величини визначався просто і не залежав від закону статистичного розподілу. Крім того необхідно, щоб відмінність теоретичного розподілу від статистичного суттєво відображалась на значенні величини. Потім задаються рівнем значимості q. Виходячи із закону розподілу випадкової величини , визначають таке її значення q, для якого виконується рівність: P( q)=q (12)

Знайдене для даної вибірки значення = q порівнюють з q. Якщо 100, a критерій 2– коли n>50. Критерій 2 є найбільш допустимий при великому числі спостережень, так як він забезпечує мінімальну помилку прийняття гіпотези в порівнянні з іншими критеріями. Його слід застосовувати в тих випадках, коли значення параметрів розподілу невідомі.

В якості випадкової величини , при використовуванні критерію 2, вибирається величина 2, яка визначається рівністю: (13), де n-кількість спостережень (об’єм вибірки); r- кількість розрядів (інтервалів на які «розбита» вибірка; mj-кількість елементів вибірки, які попали в j-ий розряд; Pj-теоретична ймовірність попадання в j-ий розряд. Вибір значення = 2q, яке визначається згідно з умовою k=r– –1, де -число невідомих параметрів теоретичного розподілу, визначаємих по даним вибірки. З знайденими за допомогою таблиці значеннями 2 порівнюють обчислене для даної вибірки за формулою значення 2. Якщо 2

Складовий критерій, регламентований ГОСТ8.207-76 застосовується для перевірки належності результатів спостережень нормальному розподілу при малому числі спостережень 15

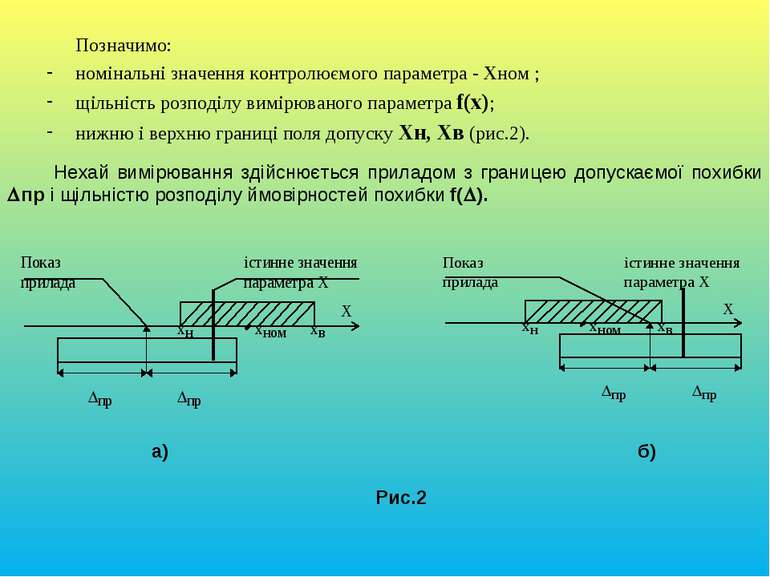
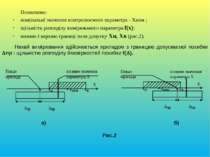
Позначимо: номінальні значення контролюємого параметра - Хном ; щільність розподілу вимірюваного параметра f(x); нижню і верхню границі поля допуску Хн, Хв (рис.2). Нехай вимірювання здійснюється приладом з границею допускаємої похибки пр і щільністю розподілу ймовірностей похибки f( ). а) б) Рис.2

З рис.2а слідує, що згідно з показом приладу приймається гіпотеза Н1 (параметр знаходиться поза полем допуску). Насправді істинне значення параметра Х знаходиться в границях поля допуску. Слід, буде допущена помилка першого роду. З мал.2б слідує, що згідно з показом приладу приймається гіпотеза Н2 (параметр Х знаходиться в полі допуску). Насправді істинне значення параметра Х знаходиться поза полем допуску. Слід, буде допущена помилка другого роду. Кількісно помилки першого та другого роду оцінюються ймовірностями їх появи.

Ймовірність допустити помилку першого роду називають ймовірністю хибної відмови Рхв , а ймовірність допустити помилку другого роду – ймовірність невизначеної відмови Рнв. Ймовірності Рхв і Рнв можуть бути знайдені за допомогою формули повної ймовірності . Рхв Рнв Висновок: Таким чином розглянуті нами критерії згоди, помилки першого і другого роду використовуються як в теоретичній метрології так і при статистичній обробці результатів вимірювань. (14) (15)