Презентація на тему:
НДІ інформаційної безпеки: презентація

Відділ Надзвичайних ситуацій

Птолемей Клеопатра

Фестський диск

ЕЗФЮ ПЛУ ЫЗОСЕЗН ЦНУГЬГЗХ ФСДСМ. ЫЗОСЕЗН ШСУСЬ, НСЁЖГ ЩГУЛХ ПЛУ. кгнусм ёогкг фесл тцфхя фзужщз фхгрзх ёогксп.

Система числення – це сукупність символів і правил їх використання для представлення чисел непозиційні позиційні

Алфавіт - 10 цифр: 0,1,2,3,4,5,6,7,8,9 Приклади запису чисел: 456=4*100+5*10+6=4*102+5*101+6*100 74,53=7*10+4*1+5*0,1+3*0,01=7*101+4*100+5*10-1+3*10-2 Десяткова система числення

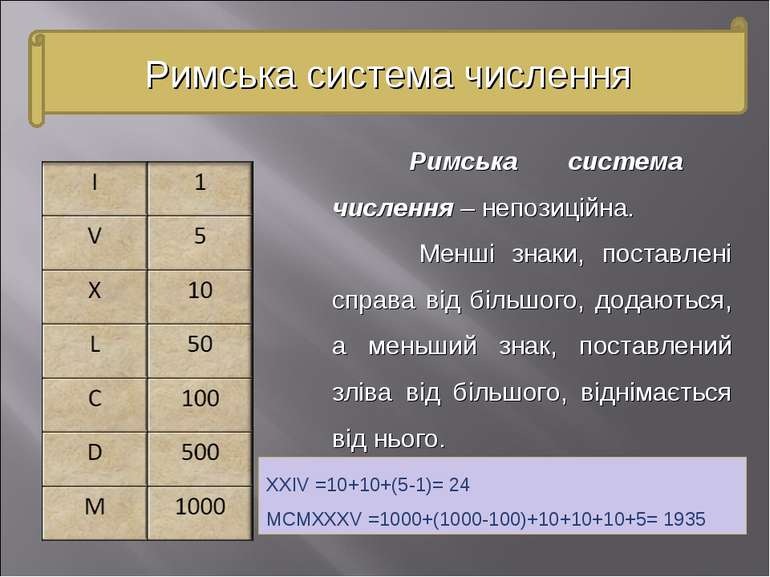
Римська система числення – непозиційна. Менші знаки, поставлені справа від більшого, додаються, а меньший знак, поставлений зліва від більшого, віднімається від нього. XXIV =10+10+(5-1)= 24 MCMXXXV =1000+(1000-100)+10+10+10+5= 1935 Римська система числення

Алфавітні системи числення - непозиційні Слов’янска нумерація була створена для переписування чисел в священних книгах північних слов’ян. Використовувалась з VIII по XIII ст.

Слов’янська кирилична алфавітна нумерація була створена разом зі словянською алфавітною системою для перекладу священних біблійських книг для словян грецькими монахами братами Кирилом і Мефодієм в IX ст. До XVII ст. ця форма запису чисел була офіційною на території сучасної Росії, Білорусії, України, Болгарії, Угорщини, Сербії і Хорватії. До сих пір православні церковні книги використовують цю нумерацію.

В давні часи в Греції була поширена так звана атична нумерація. В цій нумерації числа 1, 2, 3, 4 зображались відповідною кількістю вертикальних ліній.

Приблизно в третьому столітті до нашої ери атична нумерація в Греції була витіснена другою, так званою «Іонийскою» системою. В ній числа 1 - 9 позначаються першими літерами грецького алфавіту. Для того, щоб відрізняти цифри і букви писали рисочки над цифрами.

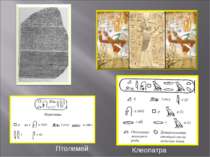
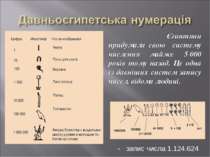
- запис числа 1.124.624 Єгиптяни придумали свою систему числення майже 5 000 років тому назад. Це одна із давніших систем запису чисел, відома людині.

Виникла вона в давньому Шумері. Походження її повязано із рахунком на пальцях. Рахували фаланги пальців на руці окрім великого. 4 пальці по три фаланги всього 12. Елементи дванадцятерічної системи числення зберіглися в Англії в системі мір (1 фут = 12 дюймів) та в грошовій системі: Английский фунт складається із 12 шиллингов. (1 шиллінг = 12 пенсам). Елементом дванадцятерічної системи в сучасному світі є рахунок дюжинами. Перші три степеня числа 12 мають власні назви: 1 дюжина = 12 штук; 1 гросс = 12 дюжин = 144 штуки; 1 маса = 12 гросів = 144 дюжины = 1728 штук. Де ви ще зустрічали рахування по 12? чайні та столові сервізи на 12 осіб в році 12 місяців на циферблаті 12 годин яйці продають по 12 штук за кордоном

Була розповсюджена: у ряді африканських племен; У Китаї. Деякі племена на філіпінських островах використовують її і в наші дні. Елементи п'ятирічної системи зберіглися в цивілізованих країнах у вигляді шкільної п'ятибальної шкали оцінок. В сказке П. П. Ершова "Конёк-Горбунок" царь, пожелав заполучить коней вступает с Иваном в торг.  Ну, я пару покупаю. Продаешь, ты? — Нет, меняю. Что в промен берешь добра? — Два — пять шапок серебра. — То есть это будет десять. Царь тотчас велел отвесить... Иван, торгуясь с царем, оперирует пятками, а более продвинутый в арифметике монарх переводит его примитивный счет в десятеричную систему.

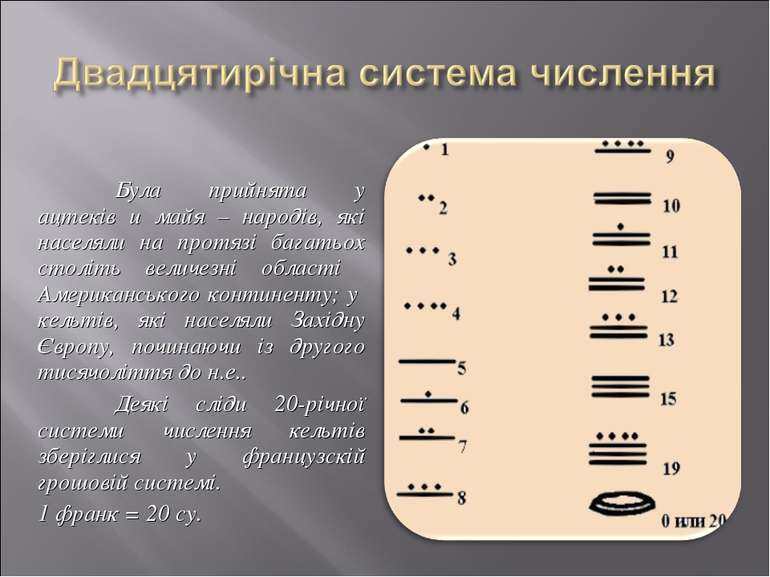
Була прийнята у ацтеків и майя – народів, які населяли на протязі багатьох століть величезні області Американського континенту; у кельтів, які населяли Західну Європу, починаючи із другого тисячоліття до н.е.. Деякі сліди 20-річної системи числення кельтів зберіглися у французскій грошовій системі. 1 франк = 20 су.

Числа, які більше за 60 записувались по розрядам, з невеликими проміжками між ними: = 1*60*60+2*60+5=3725 = 5*60+2=302 Вавілонська клінописна система числення застосовувалась ще на світанку людської цивілізації – в III тисячолітті до нашої ери. Вона поєднувала три основи – 1, 10 и 60. До наших днів зберіглися сліди рахунку шестидесятками. Адже до сьогодні ми ділимо годину на 60 хвилин, а хвилину на 60 секунд. Коло ділять на 360, тобто 6*60 градусів, градус - на 60 хвилин, а хвилину - на шістдесят секунд.

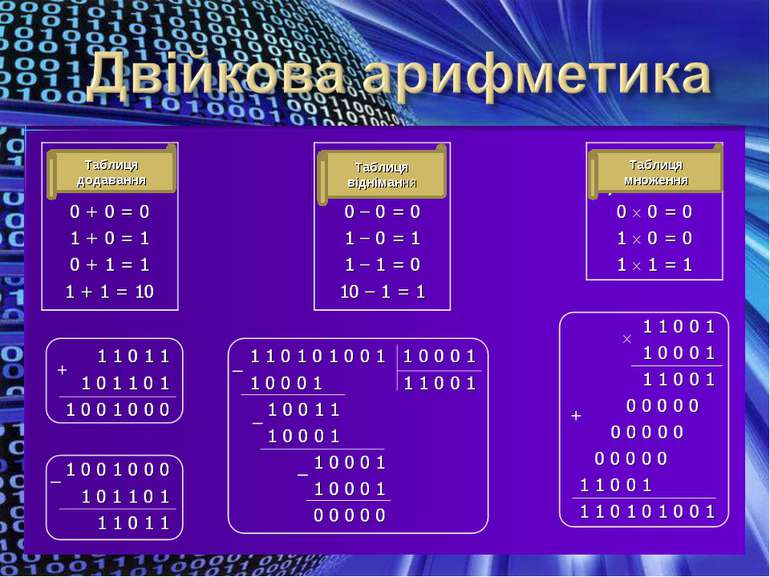
Відкриття двійкового способу представлення чисел приписуюють китайскому імператору Фо Гі, життя якого відносится до 4-го тисячоліття до нової ери. Відомий німецький математик Лейбніц (1646-1716) у 1697 р. розробив правила двійкової арифметики. Двійкова система числення знайшла застосування у якості універсального способу кодування інформації в комп'ютерах. Переваги: для її реалізації потрібні технічні пристрої з двома стійкими станами: Є струм — немає струму; намагничений— не намагничений; подання інформації за допомогою тільки двох станів надійно й завадостійко; двійкова арифметика набагато простіша десяткової. Недолік: Швидкій ріст числа розрядів, необхідних для запису чисел.

Запис числа у двійковій системі відбувається так само, як і в де сятковій: першою записується цифра ап, другою — цифра ап -1 і т. д., останньою — цифра а0. Двійковий код числа — запис цього числа у двійковій системі числення. У наведених прикладах двійкові коди мають вигляд: 0 = 02 5 = 1012 1 = 12 6 = 1102 2 = 102 7= 1112 3 = 112 25 = 110012 4 = 1002 120 = 11110002. Коефіцієнти в поданні повинні приймати тільки одне з двох значень: 0 або 1. Це забезпечує однозначність такого подання. Якщо один із коефіцієнтів більше 1, то відбувається перехід до наступного степеня числа 2.

Таблиця додавання Таблиця віднімання Таблиця множення