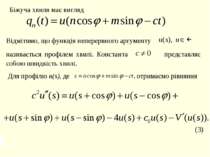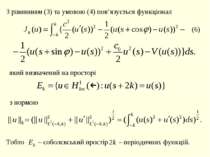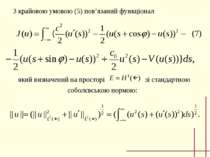Презентація на тему:
Умови існування біжучих хвиль в системі осциляторів, розміщених на цілочисловій решітці

“ Умови існування біжучих хвиль в системі осциляторів, розміщених на цілочисловій решітці. ”

Нескінченновимірні гамільтонові системи широко використовуються в нелінійній фізиці для моделювання складних оптичних і квантових явищ. Зокрема, останнім часом значну увагу приділяють моделям, дискретним за просторовою змінною. Однією з найбільш популярних моделей є нескінченний ланцюг лінійно зв’язаних нелінійних осциляторів. Серед таких систем найбільш відома модель Френкеля–Конторової, вивчена в роботах Я. Френкеля та Т. Конторової 1938 року. Ця та близькі моделі з фізичної точки зору детально вивчені О. Браном, Ю. Ківшаром, Д. Хеннінгом, Г. Ціронісом та ін. Математична ж сторона питання досліджена досить слабко. Близький клас систем Фермі–Паста–Улама вивчено досить добре такими математиками як Г. Фрісек, Дж. Воттіс, Г. Аріолі, Ф. Газзола, О. Панков та ін. В значній мірі досліджено дискретні нелінійні рівняння Шредінгера такими математиками як П. Кеврекідс, К. Расмуссен, А. Бішоп, О. Панков, М. Вейнштей та ін.

Подiбнi системи є цікавими з огляду на чисельні застосування у фiзицi. Досить важливим класом розв’язків таких систем є біжучі хвилі. Такі розв’язки виникають в багатьох задачах. * Досить детальні результати про біжучі хвилі в ланцюгах Фермі–Паста–Улама можна знайти в роботах О. Панкова. * В той же час для ланцюгів осциляторів відомі лише дві роботи Г. Йосса та К. Кіршгаснера, результати якої отримано методами теорії біфуркацій, а також дві статті С. М. Бака, в яких отримано умови існування періодичних та відокремлених біжучих хвиль. * В статтi американського вченого Srikanth P . вивчались перiодичнi розв’язки для системи осциляторiв розміщених на двовимірних решітках. * А бiжучi хвилi в таких системах вивчали грецькі математики Фекан М. і Ротос В. та американські математики Фрісек Ж. і Метьюс К. Зокрема, Фекан М. розглядав системи iз непарною - періодичною нелінійністю, а Фрісек Ж. взагалі розглядав лінійні осцилятори.

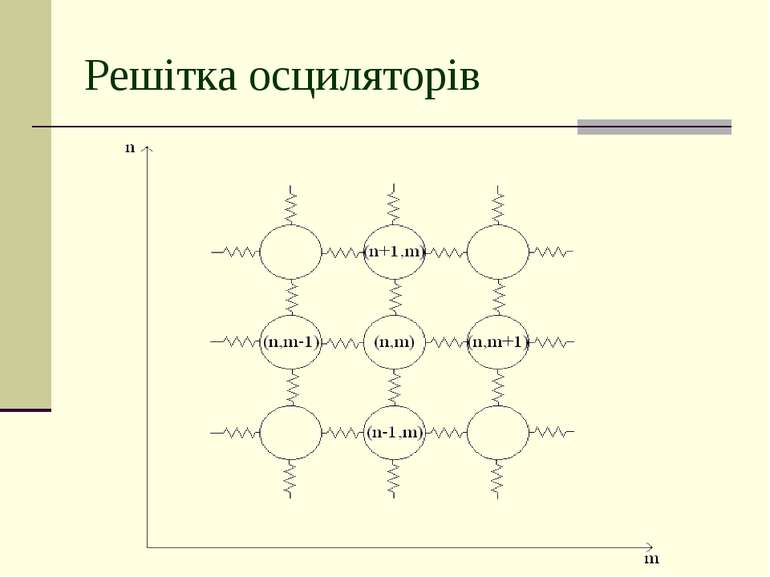
В даній роботі вивчаються рівняння, що описують динаміку нескінченної системи лінійно зв'язаних нелінійних осциляторів, розміщених на цілочисловій решітці. Нехай — узагальнена координата (n, m)-го осцилятора в момент часу t. Припускається, що кожний осцилятор лінійно взаємодіє з чотирма своїми найближчими сусідами. Рівняння руху системи, що розглядається, мають вигляд: . Рівняння (1) представляє собою нескінченну систему звичайних диференціальних рівнянь. Яку можна подати у гамільтоновому вигляді.

Решітка осциляторів

Розглянемо систему осциляторів з потенціалом: Тоді рівняння (1) набуде вигляду де - двохвимірний дискретний оператор Лапласа.

Біжуча хвиля має вигляд Для профілю u(s), де отримаємо рівняння Відмітимо, що функція неперервного аргументу називається профілем хвилі. Константа представляє собою швидкість хвилі.

Цікавими є нетривiальнi хвилi з профілем тотожно вiдмiнним від нуля. У випадку періодичних біжучих хвиль для знаходження профілю хвилi достатньо знайти розв’язок рiвняння (3) з умовою перiодичностi Профіль відокремленої хвилі є розв’язком рівняння (3) з крайовою умовою на нескінченності

Всюди далі під розв’язком рівняння (3) розуміється функція класу яка задовольняє рівняння (3) для всіх В роботі показано, що при значеннях кута який визначає напрям поширення хвилі, а саме при і задача зводиться до одновимірного випадку, який було вивчено раніше:

Всюди далі припускається, що потенціал задовольняє умову: (h) функція неперервно диференційовна, і при та існує таке що Зазначимо, що в рівнянні (3) швидкість с входить тільки в квадраті. Звідси випливає, що якщо функція u(s) задовольняє рівнянню (3), то існує дві біжучі хвилі з даним профілем та швидкостями

З рівнянням (3) та умовою (4) пов’язується функціонал який визначений на просторі з нормою Тобто – соболєвський простір – періодичних функцій.

З крайовою умовою (5) пов’язаний функціонал який визначений на просторі зi стандартною соболєвською нормою:

Неважко перевірити, що критичнi точки функцiоналiв i є – розв’язками рiвняння (3), що задовольняють умови (4) i (5) вiдповiдно. Перейдемо до основних результатів.

Iснування перiодичних бiжучих хвиль: За допомогою теореми про гiрський перевал встановлено iснування нетривiальних бiжучих хвиль з перiодичним профiлем. Для цього, згiдно сказаного вище, достатньо встановити iснування нетривiальних критичних точок функцiоналу Вiдмiтимо, що завжди є тривiальною критичною точкою та дає тривiальну бiжучу хвилю, яка тотожно рiвна нулю. Теорема Нехай виконується умова i Тодi для будь-яких i рiвняння (3) має розв’язок u, що задовольняє умові (4). Тим самим, iснують двi періодичні бiжучi хвилi з профiлем та швидкостями

Тоді існує така критична точка функціоналу І, що При цьому і Теорема (Про гірський перевал). Нехай І – функціонал класу С1 на гільбертовому просторі Н, задовольняє умову Пале-Смейла: (PS) якщо послідовність така, що обмежена, то вона містить збіжну підпослідовність. Припустимо, що існують і такі, що

Iснування вiдокремлених бiжучих хвиль: Бiжучi хвилi в даному випадку знаходяться як критичнi точки функцiоналу Функцiонал задовольняє частинi умов теореми про гiрський перевал. Однак, умова Пале–Смейла для цього функцiоналу не виконується. Тому критичнi точки в даному випадку будуються iншим способом – за допомогою переходу до границi в критичних точках функцiоналу при Теорема Нехай виконується умова i Тодi для будь-якого рiвняння (3) має розв’язок u, що задовольняє умові (5). Тим самим, iснують двi відокремлені бiжучi хвилi з профiлем та швидкостями

ВИСНОВКИ: 1) В роботі показано, що при значеннях кута який визначає напрям поширення хвилі, а саме при і задача зводиться до одновимірного випадку. 2) За допомогою методу критичних точок і за допомогою теореми про гірський перевал, отримано умови існування періодичних хвиль в системах, які розглядаються; 3) За допомогою методу критичних точок і методу періодичних апроксимацій, отримано умови існування відокремлених біжучих хвиль в системах осциляторів.

Дякуємо за увагу!