Презентація на тему:
Задачі для учнів на відсотки

НА ДОПОМОГУ ВЧИТЕЛЕВІ Підготувала вчителька математики Веселокутської ЗОШ І-ІІІ ст. Тальнівського району, Черкаської області Баранюк Наталія Петрівна

р% числа a дорівнює Розв’яжи задачу Путівка до санаторію коштує 600гривень. Службовець купує путівку за 30% її вартості. Скільки грошей він має сплатити?

Розв’язання 600грн - 100%, Х грн - 30%, Отже, службовець має сплатити 180 грн. Відповідь.180 грн.

Якщо р% якогось числа становить а, то все число дорівнює Розв’яжи задачу Службовець купив у профспілці путівку до санаторію за 30% вартості і сплатив при цьому 180 грн. Скільки коштує путівка?

Х грн. – 100%, 180грн. – 30%, Отже, путівка коштує 600грн. Відповідь.600грн.

Щоб обчислити відсоткове відношення числа а до числа в, треба знайти відношення а до в і помножити його на 100. Розв’яжи задачу Путівка до санаторію коштує 600 грн. службовець сплатив за неї 180 грн. Який відсоток вартості путівки він сплатив?

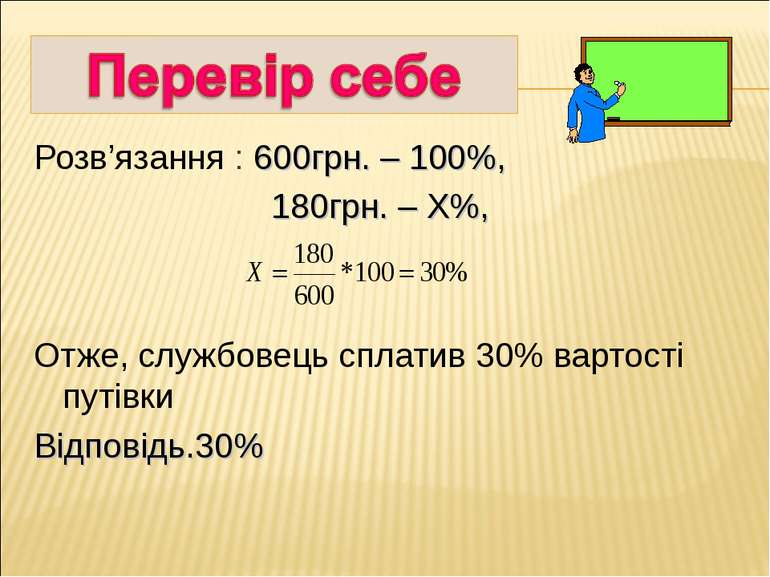
Розв’язання : 600грн. – 100%, 180грн. – Х%, Отже, службовець сплатив 30% вартості путівки Відповідь.30%

Запам'ятай!

РОЗВ’ЯЖИ ЗАДАЧУ Ціна товару спочатку знизилась на 10%, а потім ще раз на 10%. На скільки відсотків знизилася вона після двох переоцінок?

Розв’язання. Нехай початкова ціна товару Х, ціна після першого зниження 0,9Х, ціна після другого зниження У. 0,9Х – 100%, У – 90%, Х – 0,81Х = 0,19Х. Отже, ціна товару знизилася на 19%. Відповідь. На 19%.

№1. На заводі 35% усіх робітників – жінки, а решта – чоловіки, яких на заводі на 252 чоловіки більше, ніж жінок. Скільки робітників на заводі?

Розв’язання. Чоловіки становлять 100% - 35% = 65% від загальної кількості робітників. Чоловіків більше, ніж жінок на 65% - 35% = 30%,щo становить 252 чоловіки. Отже,загальна кількість робітників дорівнює Відповідь. 840 чоловік.

РОЗВ’ЯЖИ ЗАДАЧУ Від продажу товару за 1386 гривень одержано 10% прибутку. Знайти собівартість товару.

Розв’язання. Відсоток прибутку береться у відношенні до собівартості товару, яку приймемо за 100%. Ціна товару при продажі (1386грн.) становить 100%+10%=110% собівартості. Отже, собівартість дорівнює Відповідь. 1260 грн.

РОЗВ’ЯЖИ ЗАДАЧУ Вологість свіжих грибів дорівнювала 99%. Коли гриби підсушили, їх вологість знизилась до 98%. Як знизилась маса грибів?

Розв’язання. Для свіжих грибів маємо Гриби Хкг – 100%, Вода 0,99Хкг – 99%, Суха речовина 0,01Хкг – 1%. Для підсушених грибів маємо: Гриби Yкг – 100%, Вода 0,98 Y кг – 98%, Суха речовина 0,01Хкг – 2%, Х/2 Тому маса грибів зменшилась у 2 рази. Відповідь . У 2 рази.

Задане число щороку, щомісяця, щодня… збільшується чи зменшується на p% без вилучення приросту. Аn = A0(1+p/100)n Де Аn – нарощений капітал, A0 – початковий капітал, р% – відсоток річних, n – кількість років

Підприємець поклав до банку 200000грн. Під 7% річних. Які відсоткові гроші матиме підприємець через 5 років? Розв’язання. За формолою складених відсотків сума відсоткових грошей становить: А = 200000(1+7/100)≈280510(грн.) Відповідь: 80510гривень.

У хімії відсоткова концентрація називається ваговими відсотками. Якщо йдеться про об'ємні відсотки (відношення об'єму розчиненої речовини до об'єму розчину), то вживають термін міцність. Наприклад, якщо на 10 л спирту припадає 4 л чистого безводного спирту, то кажуть, що міцність цього спирту 40° (пам'ятаємо, що літр — одиниця об'єму). А якщо на 10 кг спирту припадає 4 кг чистого безводного спирту, то кажуть, що відсоткова (вагова) концентрація цього спирту 40 %. Поняття концентрації широко використовується в задачах на змішування.

До 8-ми кг 70-відсоткового розчину кислоти долили 2кг води. Визначте відсоткову концентрацію нового розчину. Розв'язання. 1)8кг розчину – 100%, Хкг кислоти– 70%, Х= 8 · 70/100=5,6(кг) кислоти в розчині. 2) 8-5,6 = 2,4(кг) води в розчині, 3)Занесемо дані в таблицю.

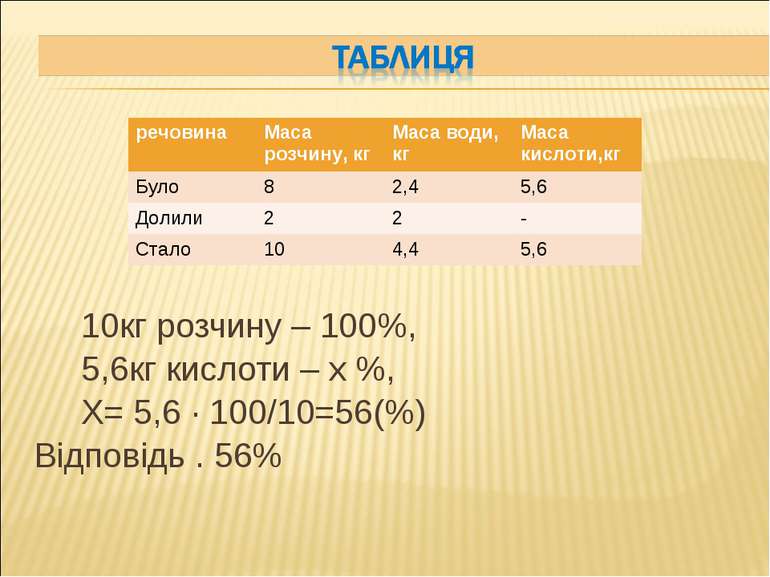
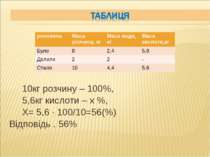
10кг розчину – 100%, 5,6кг кислоти – х %, Х= 5,6 · 100/10=56(%) Відповідь . 56% речовина Маса розчину, кг Маса води, кг Маса кислоти,кг Було 8 2,4 5,6 Долили 2 2 - Стало 10 4,4 5,6

Задача До 8 л 70-відсоткового розчину сірчаної кислоти долили 2 л води. Визначте відсоткову концентрацію нового розчину.

Розв'язання Густина 70-відсоткового розчину сірчаної кислоти ρ = 1,6. За формулою m=ρV знайдемо, що маса 8 л цього розчину дорівнює 1,6 · 8= 12,8 (кг).(Вважаємо, що маса 1л води дорівнює 1 кг.) Тоді кислоти в розчині 1,28 · 70/100=8,96(кг), а води 12,8 – 8,96 = 3,84(кг).

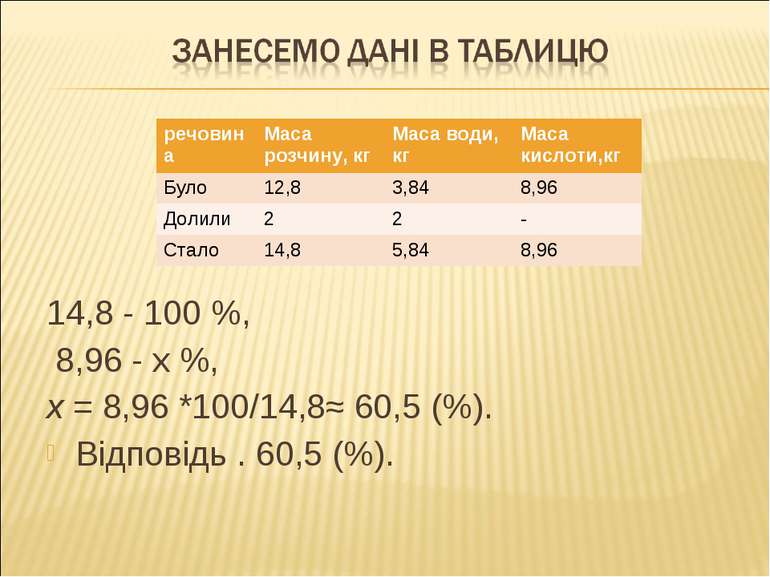
14,8 - 100 %, 8,96 - х %, х = 8,96 *100/14,8≈ 60,5 (%). Відповідь . 60,5 (%). речовина Маса розчину, кг Маса води, кг Маса кислоти,кг Було 12,8 3,84 8,96 Долили 2 2 - Стало 14,8 5,84 8,96

У задачах на суміші звичайно йдеться про маси m1, m2, ..., mк змішуваних компо-нентів та їх відсоткові концентрації р1, р2, ..., рк , а також про суміш масою М = m1 + m2 + ... + mк та її відсоткову концентрацію Р. Тоді справджується співвідношення: m1 р1 + m2 р2 + ... + mк рк = MP . Для змішування двох компонентів маємо: m1 р1 + m2 р2 = (m1 + m2) P , P = (m1 р1 + m2 р2 )/ (m1 + m2)

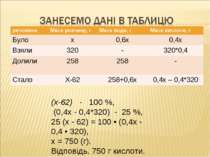
Задача . З колби, наповненої 40-відсотковою сірчаною кислотою, взяли 320 г кислоти і долили в колбу 258 г води. У результаті кон-центрація кислоти в колбі знизилася до 25 %. Визначте, скільки грамів 40-відсоткової кислоти було в колбі спочатку.

(х-62) - 100 %, (0,4х - 0,4*320) - 25 %, 25 (х - 62) = 100 • (0,4х - 0,4 • 320), х = 750 (г). Відповідь. 750 г кислоти. речовина Маса розчину, г Маса води, г Маса кислоти, г Було х 0,6х 0,4х Взяли 320 - 320*0,4 Долили 258 258 - Стало Х-62 258+0,6х 0,4х – 0,4*320

Вміст різних металів і домішок у сплавах також виражається у відсотках. Якщо, наприклад, кажуть, що чавун містить 3 % кремнію і 1 % марганцю, то це означає, що на 100 кг всього сплаву припадає 3 кг кремнію і 1 кг марганцю. Наприклад, якщо в 1 кг сплаву є 875г чистого золота,то його називають золотом 875-ї проби.

Вміст дорогоцінних металів у сплавах виражається пробою. Проба — це кількість грамів чистого золота (срібла, платини тощо) в одному кілограмі сплаву. Задача. Скільки золота 375-ї проби треба сплавити з 30г золота 750-ї проби, щоб одержати сплав золота 500-ї проби?

Розв'язання. Нехай Хг золота 375-ї проби треба сплавити з 30г золота 750-ї проби, щоб одержати сплав золота 500-ї проби. Для золота 375-ї проби маємо: Хг – 100%, mс --37,5% , тоді m1 =37,5Х/100=0,375Х(г)золота. Для золота 750-ї проби маємо: 30г – 100%, m2 --75% , тоді m2 =30*75/100=22,5(г)золота. У Yг сплаву 500-ї проби золота буде г. Маємо систему рівнянь звідки маємо,Х=60. Відповідь.60г золота 375-ї проби.

1.Скільки відсотків міді у бронзовому злитку, який містить 17кг міді і 3кг олова? 2. З молока виходить 10% сиру. Скільки молока треба, щоб вийшло 30кг сиру? 3. Через скільки років капітал, вкладений до банку під 5% річних, збільшиться у 2 рази? 4. Скільки солі розчинено у 10кг 7%-го розчину солі?

Задача 1. Латунь – сплав 60% міді і 40% цинку. Скільки міді та цинку треба взяти, щоб дістати 500т латуні? Розв’язання. 1) 500*0,6=300(кг) – міді; 2) 500:0,4 = 200(кг) – цинку. Задача 2. Ціна автомобіля спочатку підвищилась на 20%, а потім знизилась на 20%. Як змінилася ціна на автомобіль після цих двох переоцінок? Розв’язання. 20% – 20% = 0. Відповідь. Не змінилася.

Задача 1. Латунь – сплав 60% міді і 40% цинку. Скільки міді та цинку треба взяти, щоб дістати 500т латуні? Розв’язання. 1) 500*0,6=300(кг) – міді; 2) 500*0,4 = 200(кг) – цинку. Задача 2. Задача 2. Ціна автомобіля спочатку підвищилась на 20%, а потім знизилась на 20%. Як змінилася ціна на автомобіль після цих двох переоцінок? Розв’язання. Початкова ціна х грн., Ціна після підвищення 1,2хгрн. – 100%, Ціна після зниження у грн. - 80%. 1) у=1,2х * 80/100=0,96(грн), 2) Х – 0,96х = 0,04х, що становить 4%. Відповідь. Ціна знизилась на 4%..

Один кавун містить 96% води. Скільки відсотків води у 2 кавунах?

№1.Шматок сплаву міді і цинку масою 36 кг містить 45 % міді. Яку масу міді треба добавити до цього шматка, щоб новий сплав містив 60 % міді? №2. Є шматок сплаву міді й олова масою 12 кг, що містить 45 % міді. Скільки чистого олова треба додати до цього шматки, щоб одержаний сплав містив 40% міді? №3. Є брухт сталі двох сортів із вмістом нікелю 5%і 40% скільки треба взяти брухту сталі кожного сорту, щоб одержати 140т сталі, яка містить 30% нікелю? №4. скільки треба змішати 10-відсоткового і 15-відсоткового розчинів солі, щоб мати 1кг 12-відсоткового розчину?

1. Бевз Г.П. Алгебра 7-9. -- К.: Школяр, 2002. 2. Мерзляк А.Г.,Полонський В.Б., Рабинович Е.М.,Якимр М.С. Сборник задач и заданий для тематического оценивания по алгебре для 9 класса.- Х.: Гимназия, 2001. 3.Сухарева Л.С. Завдання для усної роботи, математичні диктанти та тести. Алгебра. 9 клас. - Х.: Гимназия, 2001. 4.Цыпкин А.Г. Справочник по методам решенмя задач по математике. – М.: Наука, 1989. 5. Антонов Н.П., Выгодський М.Я. Сборник задач по элементарной математике. – М.: Наука, 1974.