Презентація на тему:
Перетворення подібності та його властивості.Подібність фігур

Перетворення подібності та його властивості. Подібність фігур Гречуха Вікторія

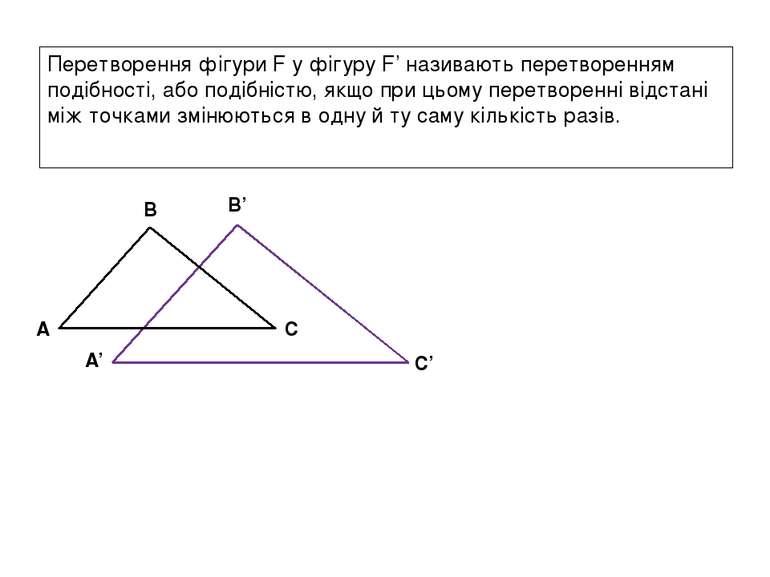
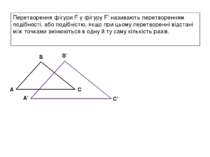
Перетворення фігури F у фігуру F’ називають перетворенням подібності, або подібністю, якщо при цьому перетворенні відстані між точками змінюються в одну й ту саму кількість разів. A B C A’ B’ C’

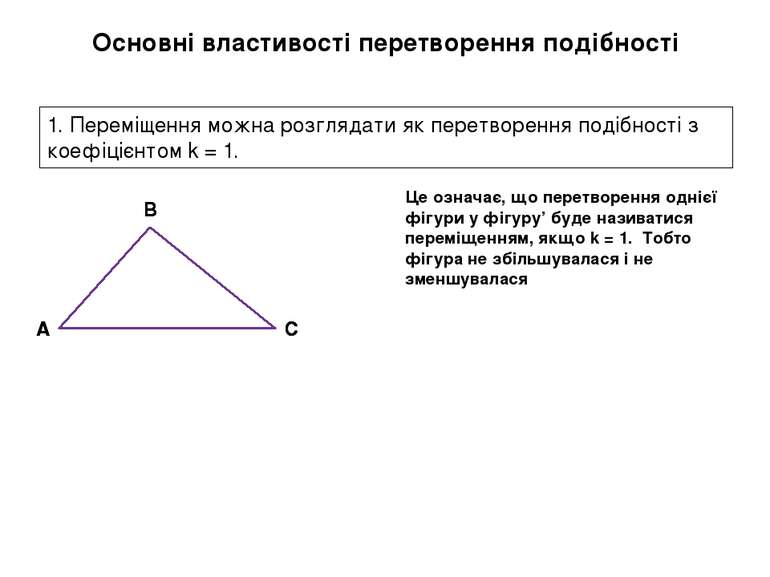
Основні властивості перетворення подібності 1. Переміщення можна розглядати як перетворення подібності з коефіцієнтом k = 1. A B C Це означає, що перетворення однієї фігури у фігуру’ буде називатися переміщенням, якщо k = 1. Тобто фігура не збільшувалася і не зменшувалася A B C

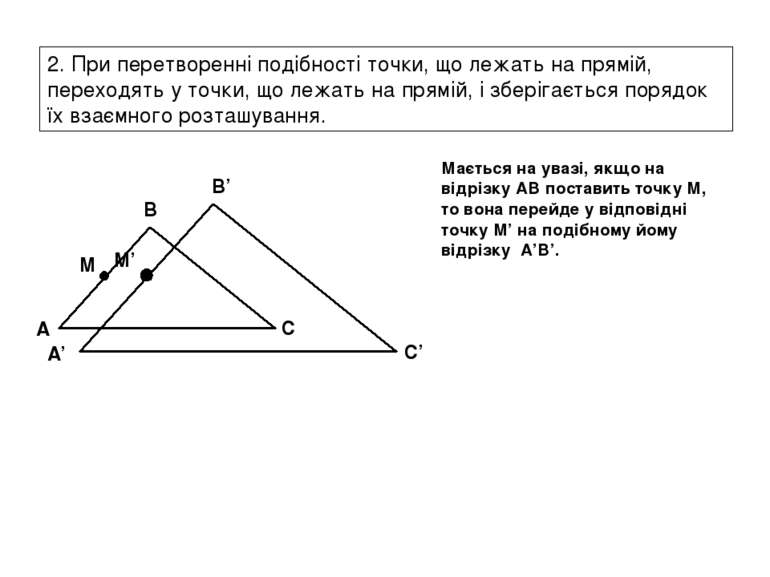
2. При перетворенні подібності точки, що лежать на прямій, переходять у точки, що лежать на прямій, і зберігається порядок їх взаємного розташування. Мається на увазі, якщо на відрізку AB поставить точку М, то вона перейде у відповідні точку М’ на подібному йому відрізку A’B’. A B C M A’ B’ C’ M’

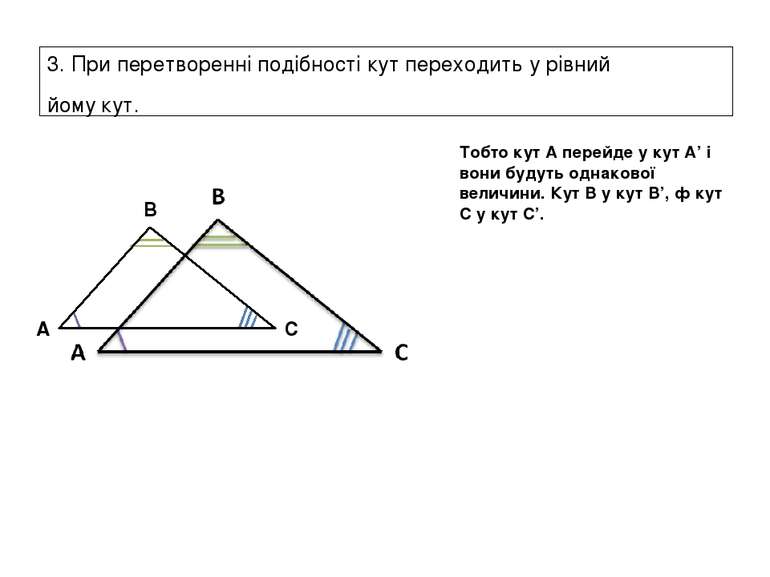
3. При перетворенні подібності кут переходить у рівний йому кут. Тобто кут А перейде у кут А’ і вони будуть однакової величини. Кут В у кут В’, ф кут С у кут С’. A B C

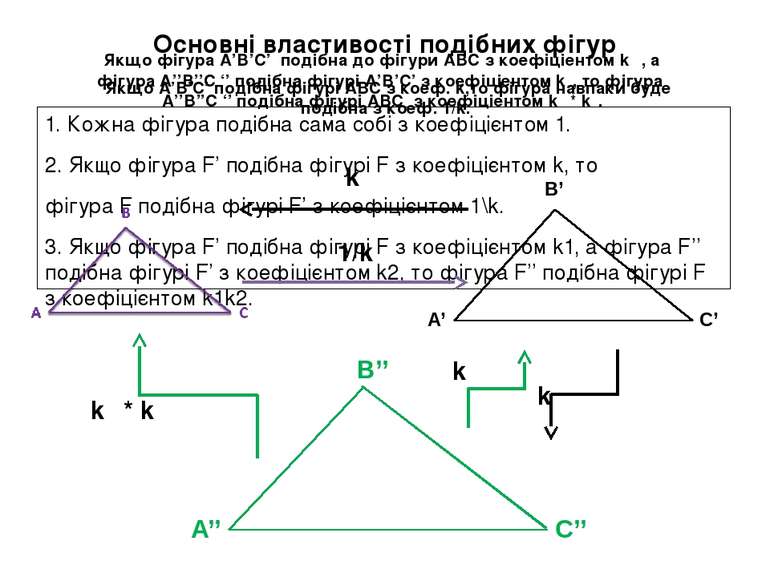
Основні властивості подібних фігур 1. Кожна фігура подібна сама собі з коефіцієнтом 1. 2. Якщо фігура F’ подібна фігурі F з коефіцієнтом k, то фігура F подібна фігурі F’ з коефіцієнтом 1\k. 3. Якщо фігура F’ подібна фігурі F з коефіцієнтом k1, а фігура F’’ подібна фігурі F’ з коефіцієнтом k2, то фігура F’’ подібна фігурі F з коефіцієнтом k1k2. Якщо A’B’C’ подібна фігурі ABC з коеф. k,то фігура навпаки буде подібна з коеф. 1/k. k 1/k Якщо фігура A’B’C’ подібна до фігури ABC з коефіціентом k₁ , а фігура A’’B’’C ‘’ подібна фігурі A’B’C’ з коефіціентом k₂, то фігура A’’B’’C ‘’ подібна фігурі ABC з коефіціентом k₁ * k₂. k₁ * k₂ k₂ k₁ A’ B’ C’ A’’ B’’ C’’

Дякую за увагу!