Презентація на тему:
"Перерізи многогранників"

Перерізи многогранників Робота Роговченко Тетяни, 10-А

Правильний багатогранник – це опуклий багатогранник з максимально можливою симетрією. Багатогранник називається правильним, якщо: він опуклий; всі його грані є рівними правильними многокутниками; в кожній його вершині сходиться однакове число граней; всі його двогранні кути рівні. Існує всього п’ять видів правильних многогранників: тетраедр(чотиригранник), куб(шестигранник), октаедр(восьмигранник), додекаедр(дванадцятигранник) та ікосаедр(двадцятигранник).

Правильні многогранники Тетраедр називається  правильним, якщо всі його грані – рівносторонні  трикутники. У правильного тетраедра всі двогранні кути при ребрах і всі тригранні кути при вершинах рівні. Кількість вершин кутів – 4. Кількість ребер – 6. Кількість граней – 4. Тетраедр (трикутна піраміда)

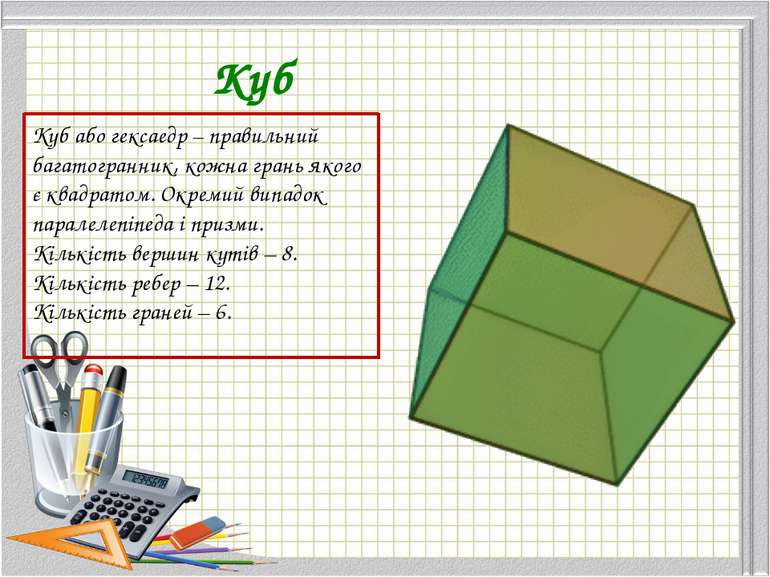
Куб Куб або гексаедр – правильний багатогранник, кожна грань якого є квадратом. Окремий випадок паралелепіпеда і призми. Кількість вершин кутів – 8. Кількість ребер – 12. Кількість граней – 6.

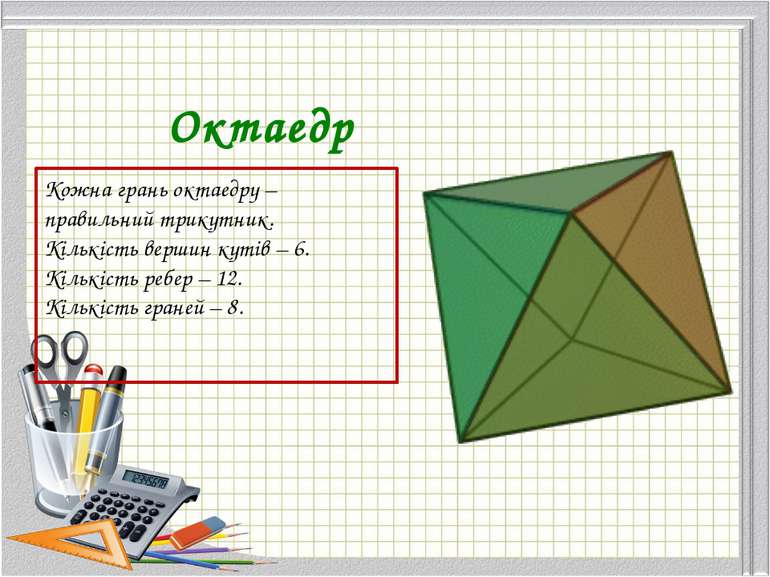
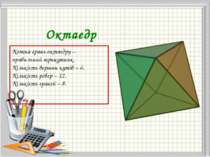
Октаедр   Кожна грань октаедру – правильний трикутник. Кількість вершин кутів – 6. Кількість ребер – 12. Кількість граней – 8.

Додекаедр – об'ємна геометрична фігура, складена з дванадцяти правильних п'ятикутників. Кількість вершин кутів – 20. Кількість ребер – 30. Кількість граней – 12. Додекаедр

В ікосаедрі кожна грань є правильним трикутником. Кількість вершин кутів – 20. Кількість ребер – 30. Кількість граней – 12. Ікосаедр

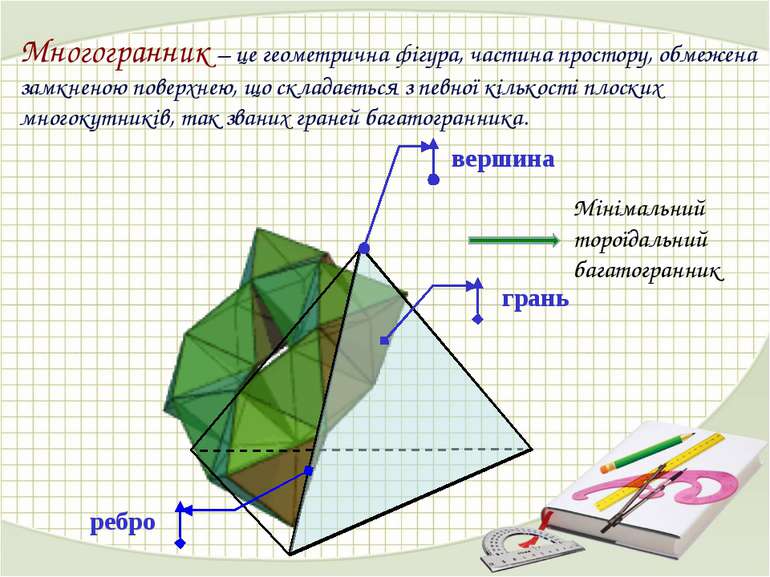
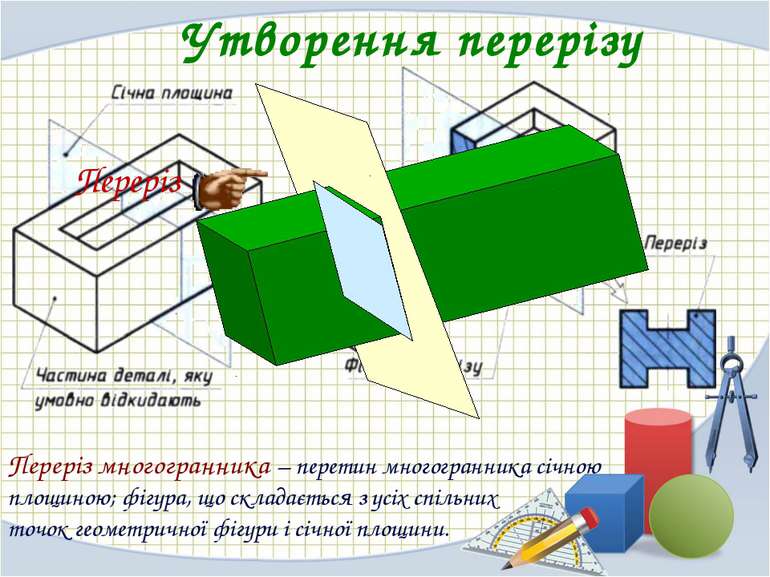
Утворення перерізу Переріз многогранника – перетин многогранника січною площиною; фігура, що складається з усіх спільних точок геометричної фігури і січної площини. Переріз

Площину перерізу можна задати: 1. Трьома точками, що не лежать на одній прямій. 2. Прямою і точкою, що не лежить на ній. 3. Двома прямими, що перетинаються. 4. Двома паралельними прямими.

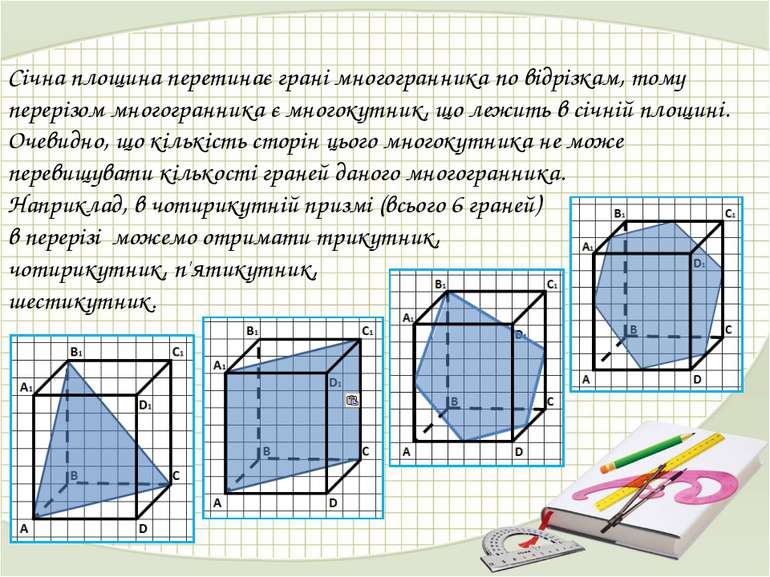
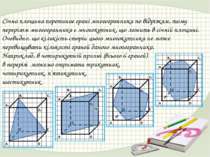
Січна площина перетинає грані многогранника по відрізкам, тому перерізом многогранника є многокутник, що лежить в січній площині. Очевидно, що кількість сторін цього многокутника не може перевищувати кількості граней даного многогранника. Наприклад, в чотирикутній призмі (всього 6 граней) в перерізі можемо отримати трикутник, чотирикутник, п'ятикутник, шестикутник.

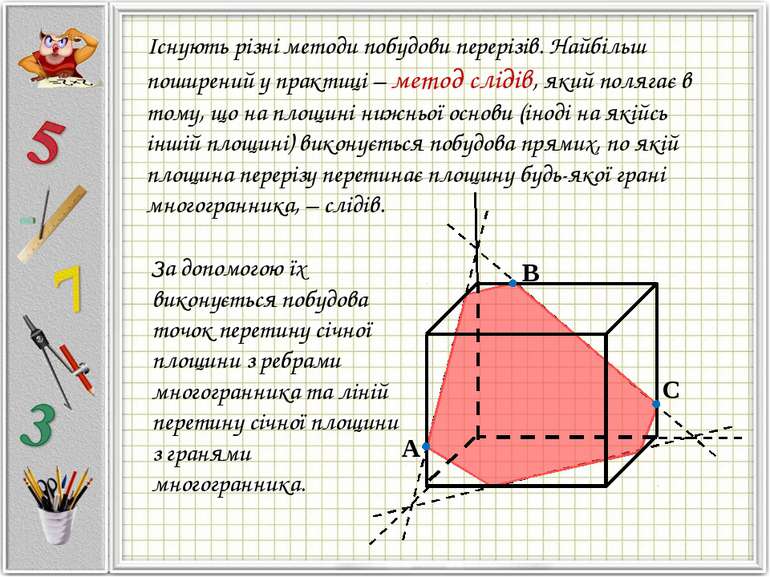
Існують різні методи побудови перерізів. Найбільш поширений у практиці – метод слідів, який полягає в тому, що на площині нижньої основи (іноді на якійсь іншій площині) виконується побудова прямих, по якій площина перерізу перетинає площину будь-якої грані многогранника, – слідів. За допомогою їх виконується побудова точок перетину січної площини з ребрами многогранника та ліній перетину січної площини з гранями многогранника.

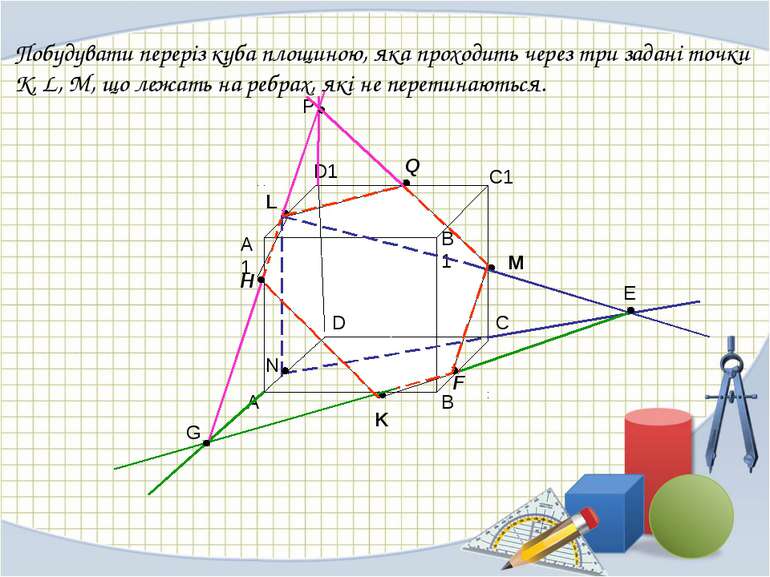
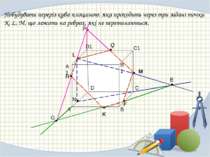
A B C D A1 B1 D1 C1 N E F G P H Q Побудувати переріз куба площиною, яка проходить через три задані точки K, L, M, що лежать на ребрах, які не перетинаються. L M K

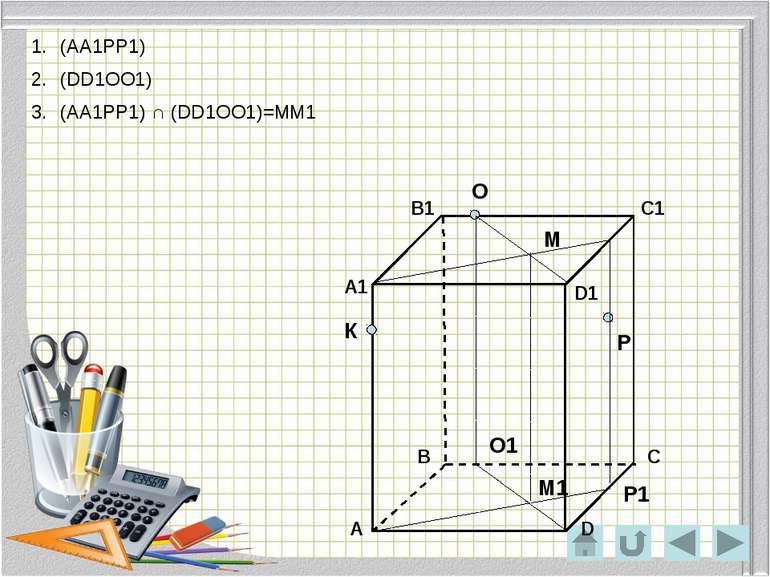
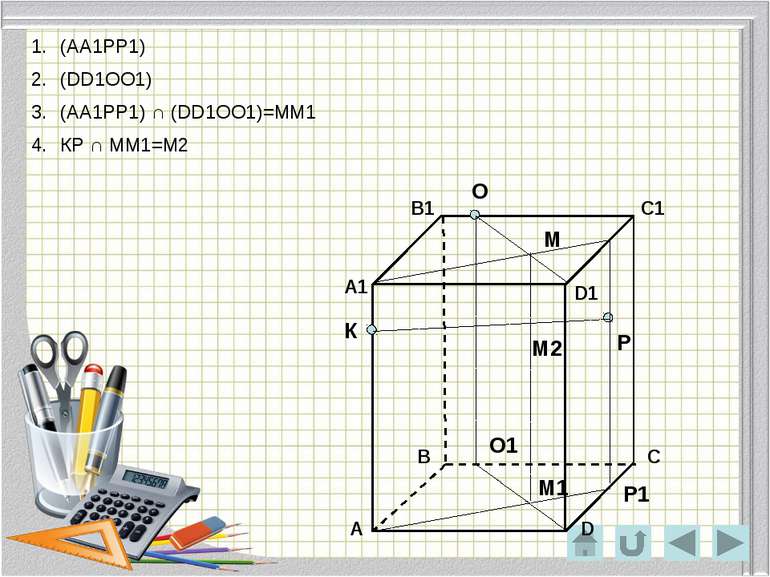
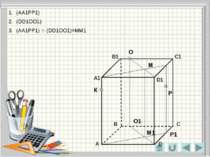
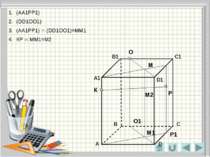
О Р К Метод зручний при побудові перерізів в тих випадках, коли незручно знаходити слід січної площини. Побудувати переріз через точки К,Р,О. (АА1РР1) (DD1ОО1) Р1 Площина (DD1ОО1) визначається паралельними прямими DD1 і OO1. Площина (АА1РР1) визначається паралельними прямими АА1 і РР1. О1 Метод внутрішнього проектування

О Р К Р1 О1 М М1 (АА1РР1) (DD1ОО1) (АА1РР1) ∩ (DD1ОО1)=ММ1

О Р К Р1 О1 (АА1РР1) (DD1ОО1) (АА1РР1) ∩ (DD1ОО1)=ММ1 КР ∩ ММ1=М2 М М1 М2

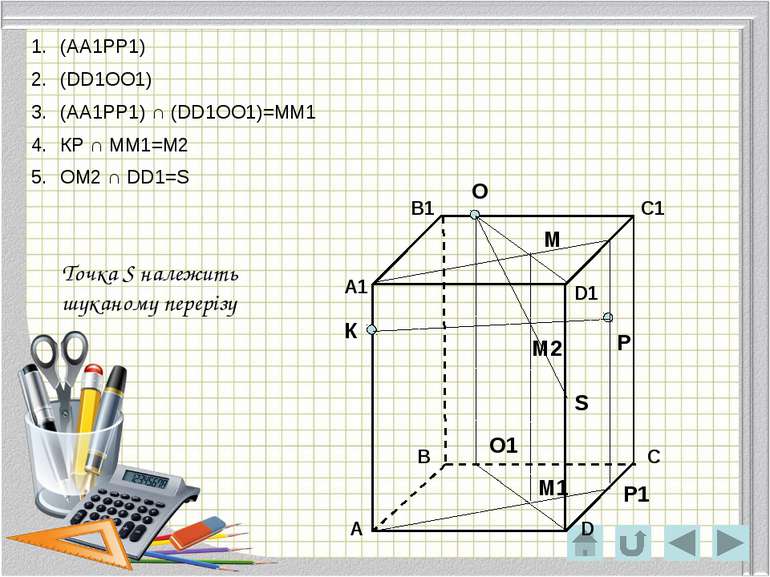
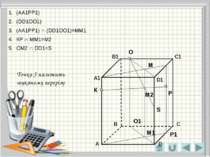
О Р К Р1 О1 М М1 М2 S Точка S належить шуканому перерізу (АА1РР1) (DD1ОО1) (АА1РР1) ∩ (DD1ОО1)=ММ1 КР ∩ ММ1=М2 ОМ2 ∩ DD1=S

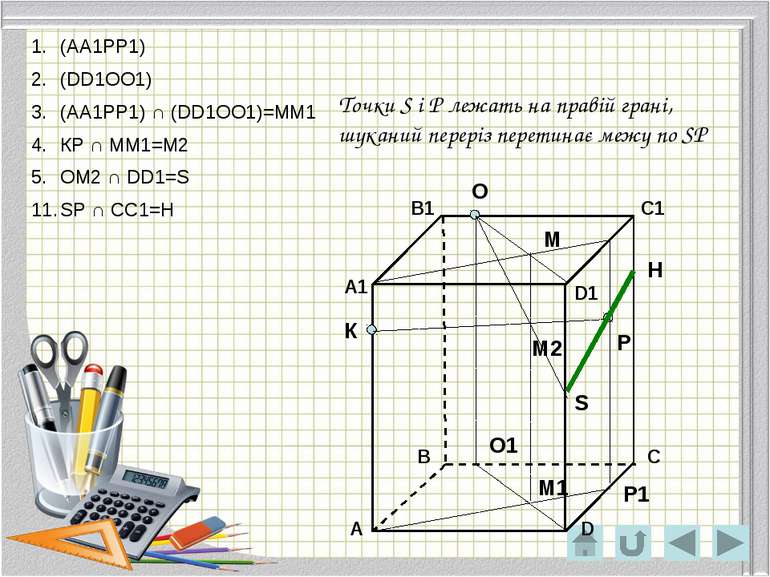
О Р К Р1 О1 М М1 М2 S (АА1РР1) (DD1ОО1) (АА1РР1) ∩ (DD1ОО1)=ММ1 КР ∩ ММ1=М2 ОМ2 ∩ DD1=S SP ∩ CC1=H H Точки S і Р лежать на правій грані, шуканий переріз перетинає межу по SР

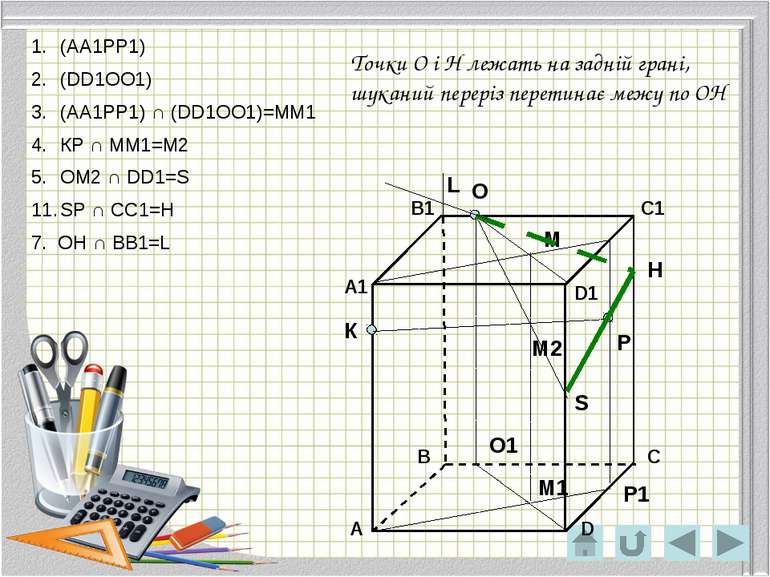
О Р К Р1 О1 М М1 М2 S H Точки O і H лежать на задній грані, шуканий переріз перетинає межу по OH (АА1РР1) (DD1ОО1) (АА1РР1) ∩ (DD1ОО1)=ММ1 КР ∩ ММ1=М2 ОМ2 ∩ DD1=S SP ∩ CC1=H 7. OH ∩ BB1=L L

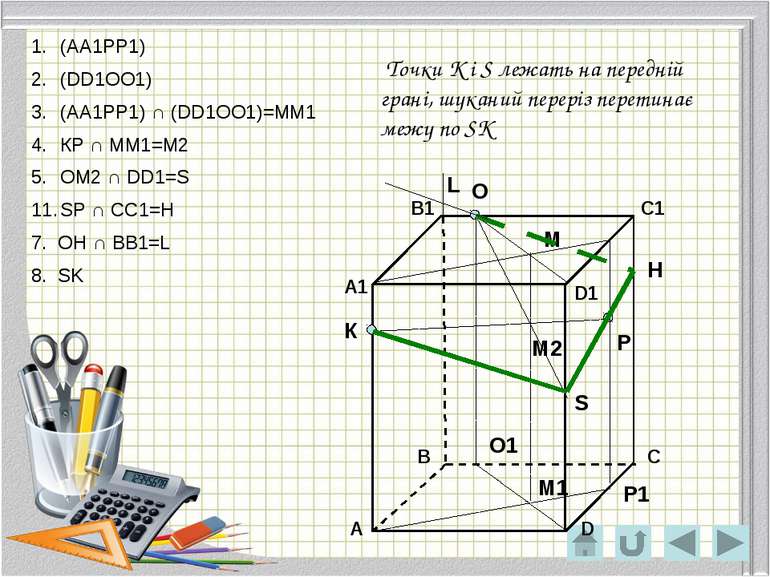
О Р К Р1 О1 М М1 М2 S H Точки К і S лежать на передній грані, шуканий переріз перетинає межу по SK (АА1РР1) (DD1ОО1) (АА1РР1) ∩ (DD1ОО1)=ММ1 КР ∩ ММ1=М2 ОМ2 ∩ DD1=S SP ∩ CC1=H 7. OH ∩ BB1=L 8. SK L

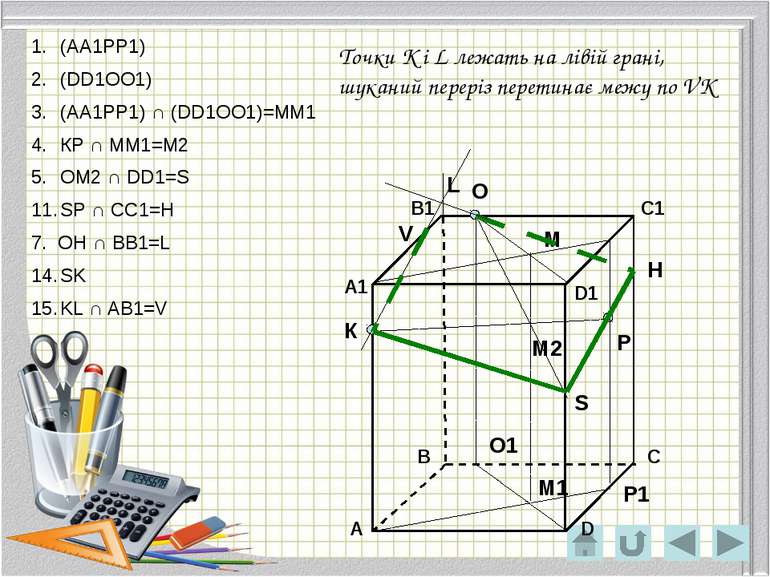
О Р К Р1 О1 М М1 М2 S H Точки K і L лежать на лівій грані, шуканий переріз перетинає межу по VK L V (АА1РР1) (DD1ОО1) (АА1РР1) ∩ (DD1ОО1)=ММ1 КР ∩ ММ1=М2 ОМ2 ∩ DD1=S SP ∩ CC1=H 7. OH ∩ BB1=L SK KL ∩ AB1=V

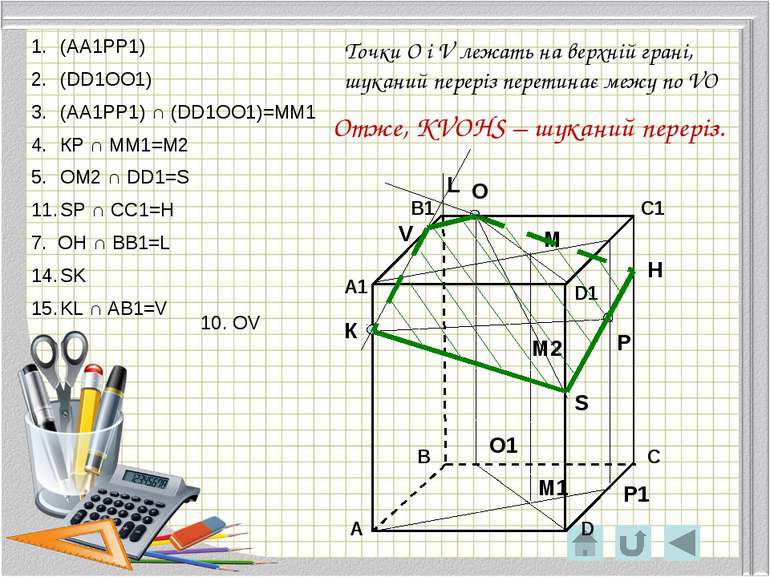
О Р К Р1 О1 М М1 М2 S H Точки O і V лежать на верхній грані, шуканий переріз перетинає межу по VO L V Отже, KVOHS – шуканий переріз. (АА1РР1) (DD1ОО1) (АА1РР1) ∩ (DD1ОО1)=ММ1 КР ∩ ММ1=М2 ОМ2 ∩ DD1=S SP ∩ CC1=H 7. OH ∩ BB1=L SK KL ∩ AB1=V 10. OV

Практичне значення перерізів Перерізи найчастіше застосовують для того, щоб показу вати поперечну форму предметів (рукояток, гайкових клю чів, слюсарних інструментів, деталей з прокату різного про філю) та форму отворів, заглибин, зрізів та вирізів на повер хнях округлих деталей тощо. Перерізи є невід’ємною частиною нашого повсякденного життя, вони зустрічаються у різних ситуаціях: у побуті, у столярстві, токарстві і т.д. Також перерізи використовуються у кресленні, конструкторській практиці.

Дякую за увагу!