Презентація на тему:
Означення властивостей геометричной прогресії

Тема 6 Арифметична та геометрична прогресії Числові послідовності. Властивості числових послідовностей Арифметична прогресія. Формула n-го члена арифметичної прогресії Сума перших n членів арифметичної прогресії Геометрична прогресія. Формула n-го члена геометричної прогресії Сума перших n членів геометричної прогресії Нескінченна геометрична прогресія (|q| < 0) та її сума Розв’язування вправ

Пункт 11.1. Пригадайте 1. Яку числову послідовність називають арифметичною прогресією? 2. Чи можуть члени арифметичної прогресії дорівнювати нулю? 3. Чи може різниця арифметичної прогресії дорівнювати нулю? Означення і властивості геометричної прогресії

Приклад 1. Знайти шостий член геометричної прогресії, перший член якої дорівнює 8, а знаменник становить 1/2. Розв'язання. b6 = b1q5; Приклад 2. Другий член геометричної прогресії дорівнює 1/27, a п'ятий член дорівнює 1. Знайти перший член і знаменник прогресії. Розв'язання. b2 = b1q, b5 = b1q4 b1 знаходимо з рівності b2 = b2 q Формула n-го члена геометричної прогресії

Розглянемо числові послідовності: 1) 1; 2; 4; 8; 16; ...; Особливість цих послідовностей полягає в тому, що кожний наступний член є результатом множення попереднього члена на одне й те саме для даної послідовності число. Зокрема, кожен член першої послідовності множили на 2; другої — на ; третьої — на . Поняття геометричної прогресії

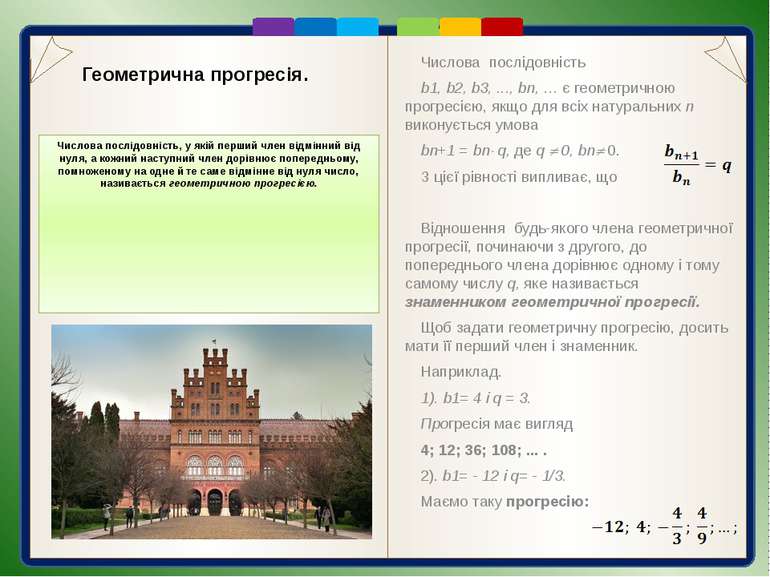
Числова послідовність b1, b2, b3, ..., bn, … є геометричною прогресією, якщо для всіх натуральних n виконується умова bn+1 = bn q, де q 0, bn 0. З цієї рівності випливає, що Відношення будь-якого члена геометричної прогресії, починаючи з другого, до попереднього члена дорівнює одному і тому самому числу q, яке називається знаменником геометричної прогресії. Щоб задати геометричну прогресію, досить мати її перший член і знаменник. Наприклад. 1). b1= 4 і q = 3. Прогресія має вигляд 4; 12; 36; 108; ... . 2). b1= - 12 і q= - 1/3. Маємо таку прогресію: Числова послідовність, у якій перший член відмінний від нуля, а кожний наступний член дорівнює попередньому, помноженому на одне й те саме відмінне від нуля число, називається геометричною прогресією. Геометрична прогресія.

Встановимо формулу загального члена геометричної прогресії b1, b2, b3, ..., bn, … Згідно з означенням геометричної прогресії, b2 = b1 q b3 = b2 q b4 = b3 q ………………. bn-1 = bn-2 q bn = bn-1 q Помноживши почленно ці рівності, маємо: b2 b3 ... bn-1 bn= b1 b2 b3 … bn-2 bn-1 qn-1 Поділимо обидві частини одержаної рівності на підкреслений добуток. Отримаємо шукану формулу: bn = b1 qn-1 Формула n-го члена геометричної прогресії bn = b1 qn-1

Приклад 3. Знайти четвертий член геометричної прогресії (bn), якщо п'ятий її член дорівнює -6, а сьомий член дорівнює -54. Розв'язання. Виразимо сьомий член прогресії через її п'ятий член і знаменник. Маємо: b7 = b5 q2. Звідси 3 рівняння q2 = 9 маємо два значення q: q1 = З, q2 = - З. Щоб знайти четвертий член прогресії, досить п'ятий член поділити на q. Якщо q = З, то b4 = (-6)/3=-2 якщо q = -3, то b4 = (-6)/(-3)=2 Отже, отримали два розв'язки: bn = -2, bn - 2. Геометрична прогресія. Формула n-го члена геометричної прогресії

Геометрична прогресія має наступні властивості. 1. Будь-який член геометричної прогресії, починаючи з другого, є середнім пропорційним, (геометричним) двох сусідніх з ним, членів. Тобто квадрат кожного члена геометричної прогресії, крім першого, дорівнює добутку двох сусідніх з ним членів. Якщо bm-1, bm, bm+1 - три послідовні члени геометричної прогресії, то Властивості геометричної прогресії Будь-який член геометричної прогресії, починаючи з другого, є середнім пропорційним, (геометричним) двох сусідніх з ним, членів.

2. Властивості геометричної прогресії Будь-який член геометричної прогресії, починаю чи з другого, є середнім пропорційним, (геометричним) двох сусідніх з ним, членів. 2. Добуток двох членів скінченної геометричної прогресії, рівновіддалених від крайніх членів, дорівнює добутку крайніх членів. Доведемо цю властивість у загальному вигляді. Доведення. Нехай геометрична прогресія (bn) має n членів. Члени прогресії, що стоять на k-му місці від початку та на k-му місці від її кінця, відповідно дорівнюють: bk=b1 qk-1 bn-k+1=b1 qn-k Утворимо їх добуток: bk bn-k+1 = b1 qk-1 b1 qn-k = b1 b1 qn-1= = b1 bn, що й треба було довести.

Яку числову послідовність називають геометричною прогресією? Що називають знаменником геометричної прогресії? Чи може хоча б один член геометричної прогресії дорівнювати нулю? Як обчислити будь-який член геометричної прогресії, знаючи її перший член і знаменник? Запитання для самоперевірки

Геометрична прогресія має наступні властивості. Геометрична прогресія має наступні властивості. 1. Будь-який член геометричної прогресії, починаючи з другого, є середнім пропорційним, (геометричним) двох сусідніх з ним, членів. Тобто квадрат кожного члена геометричної прогресії, крім першого, дорівнює добутку двох сусідніх з ним членів. Якщо bm-1, bm, bm+1 - три послідовні члени геометричної прогресії, то

2. 2.

Яку числову послідовність називають геометричною прогресією? Яку числову послідовність називають геометричною прогресією? Що називають знаменником геометричної прогресії? Чи може хоча б один член геометричної прогресії дорівнювати нулю? Як обчислити будь-який член геометричної прогресії, знаючи її перший член і знаменник?