Презентація на тему:
Многокутник та його властивості

Многокутник та його властивості

Многокутник Замкнена ламана лінія Фігура, яка складається з відрізків ,розміщених так, що суміжні відрізки не лежать на одній прямій, а несуміжні – не мають спільних точок. це

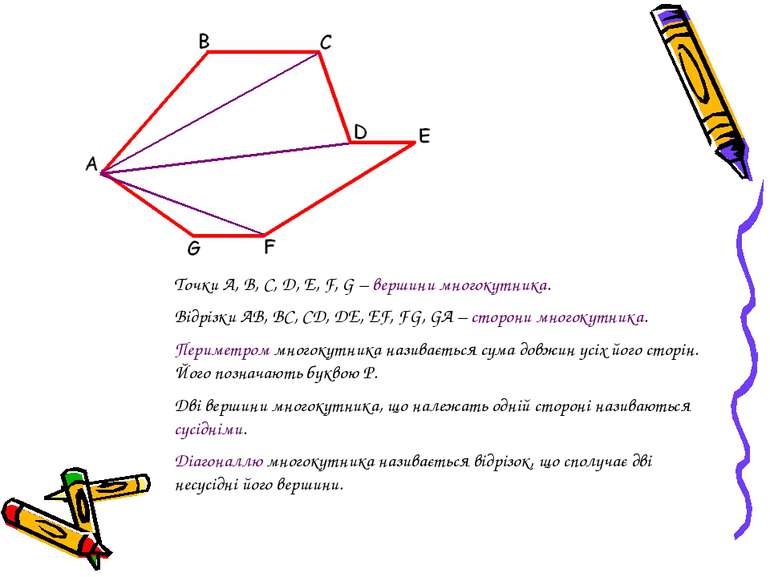
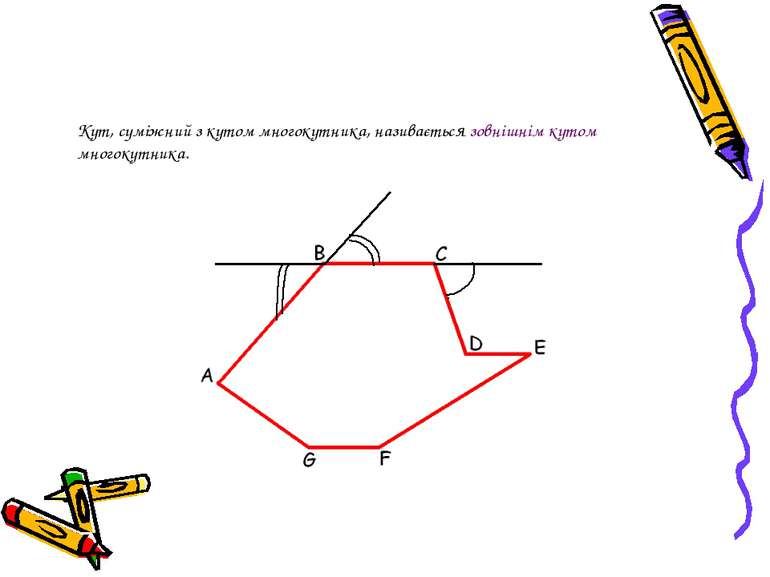
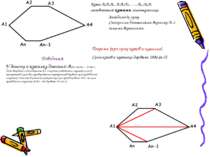
Точки А, В, С, D, Е, F, G – вершини многокутника. Відрізки АВ, ВС, CD, DE, EF, FG, GA – сторони многокутника. Периметром многокутника називається сума довжин усіх його сторін. Його позначають буквою Р. Дві вершини многокутника, що належать одній стороні називаються сусідніми. Діагоналлю многокутника називається відрізок, що сполучає дві несусідні його вершини.

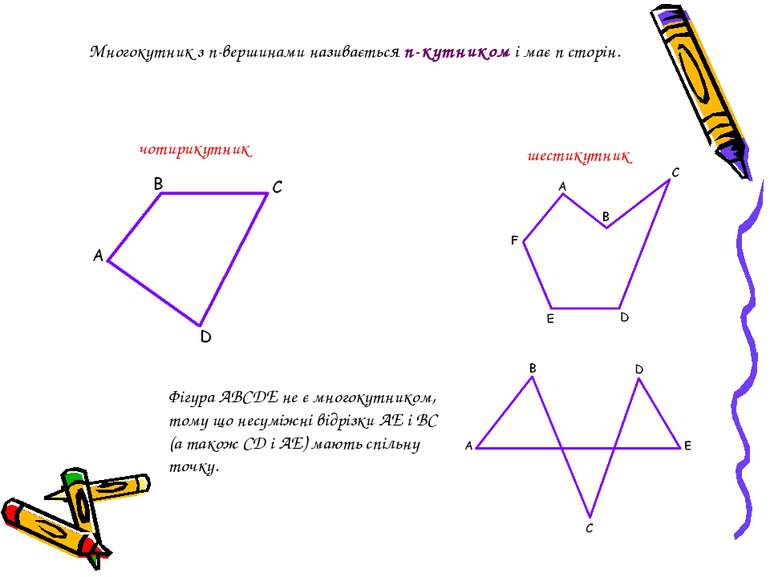
Многокутник з n-вершинами називається n-кутником і має n сторін. Фігура ABCDE не є многокутником, тому що несуміжні відрізки AE і BC (а також СD і AE) мають спільну точку. чотирикутник шестикутник

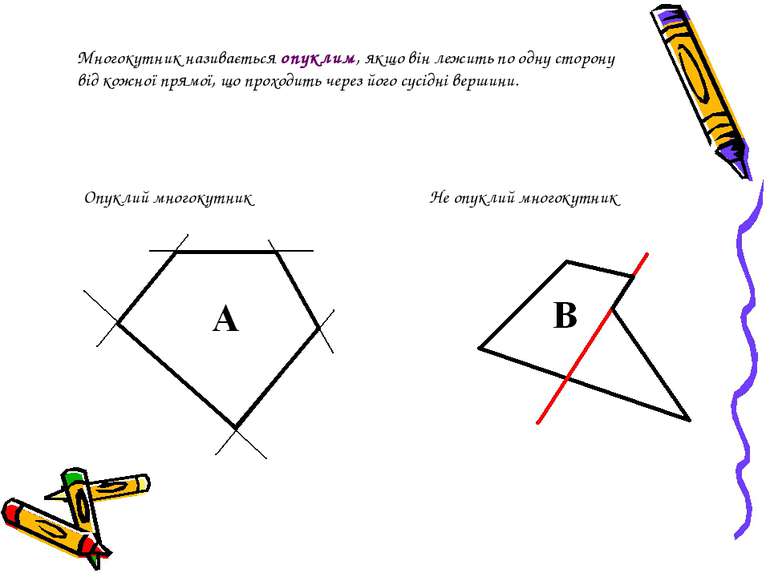
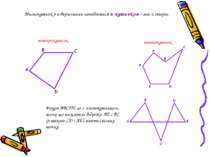
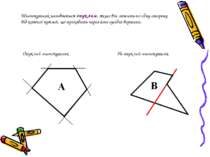
Многокутник називається опуклим, якщо він лежить по одну сторону від кожної прямої, що проходить через його сусідні вершини. Опуклий многокутник Не опуклий многокутник

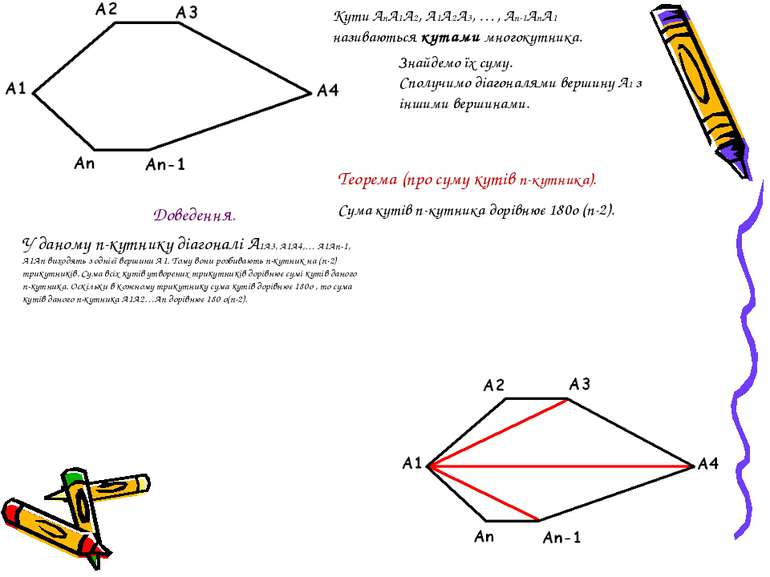
Кути АnА1А2, А1А2А3, …, Аn-1АnА1 називаються кутами многокутника. Знайдемо їх суму. Сполучимо діагоналями вершину А1 з іншими вершинами. Доведення. У даному n-кутнику діагоналі А1А3, А1А4,… А1Аn-1, А1Аn виходять з однієї вершини А1. Тому вони розбивають n-кутник на (n-2) трикутників. Сума всіх кутів утворених трикутників дорівнює сумі кутів даного n-кутника. Оскільки в кожному трикутнику сума кутів дорівнює 180о , то сума кутів даного n-кутника А1А2…Аn дорівнює 180 o(n-2). Теорема (про суму кутів n-кутника). Сума кутів n-кутника дорівнює 180о (n-2).

Кут, суміжний з кутом многокутника, називається зовнішнім кутом многокутника.

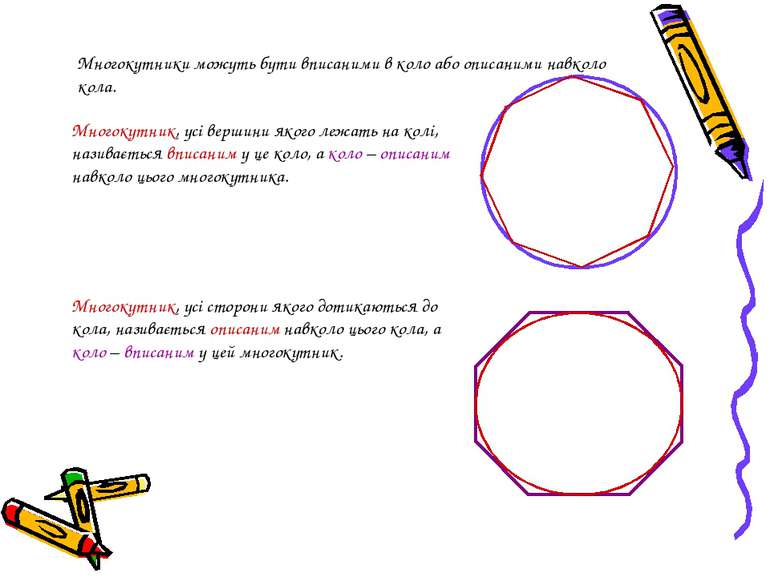
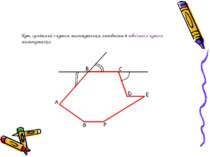
Многокутники можуть бути вписаними в коло або описаними навколо кола. Многокутник, усі вершини якого лежать на колі, називається вписаним у це коло, а коло – описаним навколо цього многокутника. Многокутник, усі сторони якого дотикаються до кола, називається описаним навколо цього кола, а коло – вписаним у цей многокутник.

Задача №1 Знайдіть периметр n-кутника, якщо у нього всі сторони дорівнюють по 2 см і: 1) n=7; 2) n=10; 3) n=9; Периметр n-кутника обчислюється за формулою: Рn=а •n 1. n=7, а=2; Р7= 7 •2=14; 2. n=10, а=2; Р10= 10 •2=20; 3. n=9, а=2; Р9= 9 •2=18;

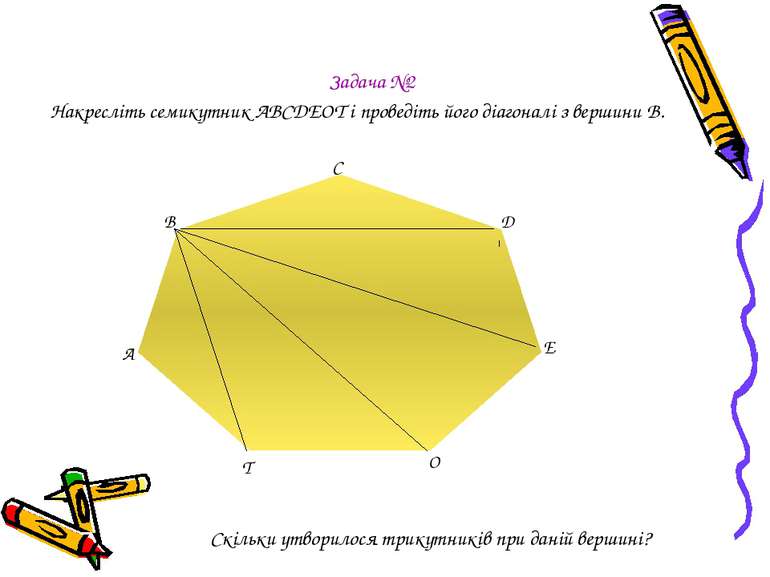
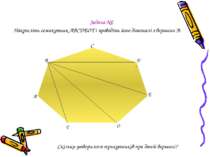
Задача №2 Накресліть семикутник АВСDEOT і проведіть його діагоналі з вершини В. С В А D E O T Скільки утворилося трикутників при даній вершині?

Задача №3 Чому дорівнює сума кутів: п’ятикутника; дев’ятикутника? Сума кутів n-кутника дорівнює 180о (n-2). При n=5 маємо: 180о (n-2)=180о (5-2)=540о 2. При n=9 маємо: 180о (n-2)=180о (9-2)=1260о

Задача №4 Скільки вершин у n-кутника, якщо кожен його кут дорівнює 144о Розв’язання Нехай а–кут n-кутника. α=144 о Сума кутів n-кутника визначимо як 144о•n або за формулою 180о (n-2). Прирівняємо: 144о•n= 180о (n-2) і знайдемо n. n=10.

Задача №5 Знайдіть зовнішній кут при вершині n-кутника, якщо кожен його кут дорівнює 144о? 144о ? Розв’язання Нехай кут а= 144о. Позначимо зовнішній кут n-кутника через β. Тоді β= 180о -144о =36о