Презентація на тему:
Логарифмічна функція і параметр

Заняття факультатива Тема: Логарифмічна функція і параметр Вчитель Цюрупинської спеціалізованої школи І-ІІІст. №4 Цуцман В.Я.

Актуальність теми: Логарифмічні рівняння і нерівності з параметрами зустрічаються в завданнях ЗНО і ДПА Вміння розв’язувати такі завдання сприяють одержанню вищого балу при написанні відповідної роботи

Мета заняття: Згадати властивості логарифмів і логарифмічної функції; етапи розв’язання нерівностей методом інтервалів; умови залежності знака квадратного тричлена від дискримінанта і знака старшого коефіцієнта

Алгоритм розв’язування логарифмічних рівнянь і нерівностей з параметрами: 1. Знайти область визначення виразу f(x)>0; g(x)>0; f(x)=g(x) f(x)>0; або f(x)>0; g(x)>0; g(x)>0; с>1; 0

2. Розв’язати звичайне логарифмічне рівняння або логарифмічну нерівність 3. Чітко пам’ятати властивості: а) б) loga²b=½ logІаІb b>0 logab2=2loga|b| a>0 a ≠ 1 loga(bc)=logaІbІ+logaІсІ a>0 a≠1 loga(b/c)=logaІbІ–logaІсІ a>0 a≠1 с≠0

4. Застосування графічного методу розв’язання рівнянь і нерівностей 5. Раціональні способи знаходження коренів квадратного рівняння, позначення коренів на числовій осі, розв’язування квадратичних нерівностей 6. Дослідження граничних значень параметрів і правильний запис відповіді

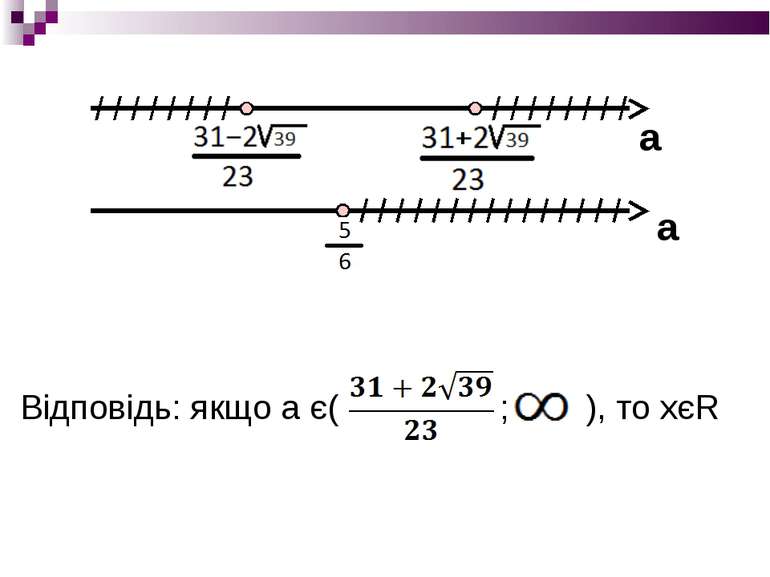
Завдання №1 Розв’язати рівняння: Розв'язання: Дане рівняння має корені при умові: Відповідь: якщо а=1, то х=-1; якщо а≠1, то хєØ Іlog3(x+2)І= –(x+a)2 log3(x+2)=0; -(x+a)2=0

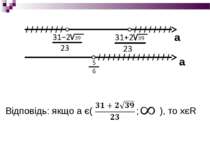
Завдання №2 Знайти значення а, при яких функція f(x)=lg((6a–5)x2–5(a–1)x+2a – 3) визначена при будь-якому дійсному значенні х, тобто х є R Розв'язання: Знаходимо область визначення даної функції: D: (6a-5)x2-5(a-1)x+2a-3>0 Дана нерівність виконується за умови: D0

Відповідь: якщо а є( ; ), то хєR а а

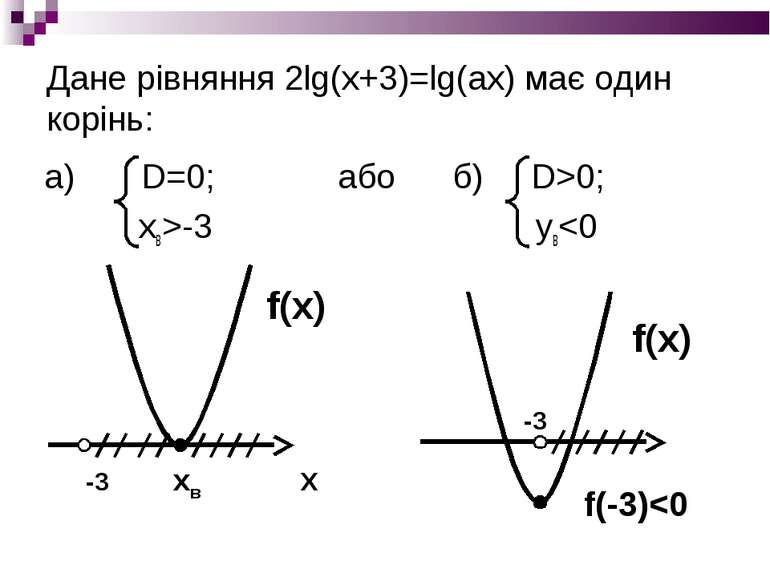
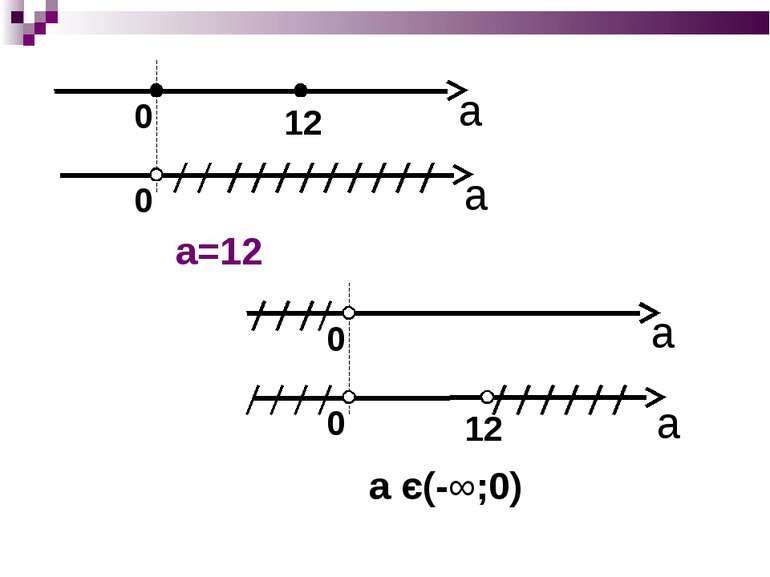
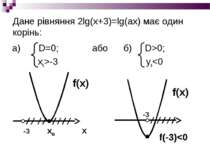
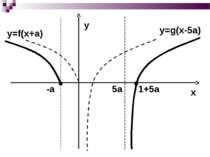
Завдання №3 Знайти всі значення параметра а, при яких рівняння 2lg(x+3)=lg(ax) має єдиний розв′язок Розв'язання: D(у): x+3>0; (x+3)2=ax; ax>0 Розглянемо функцію y=x2+(6-a)x+9 на проміжку (-3; ∞)

Дане рівняння 2lg(x+3)=lg(ax) має один корінь: а) D=0; або б) D>0; xв>-3 yв

а а a=12 а а а є(-∞;0)

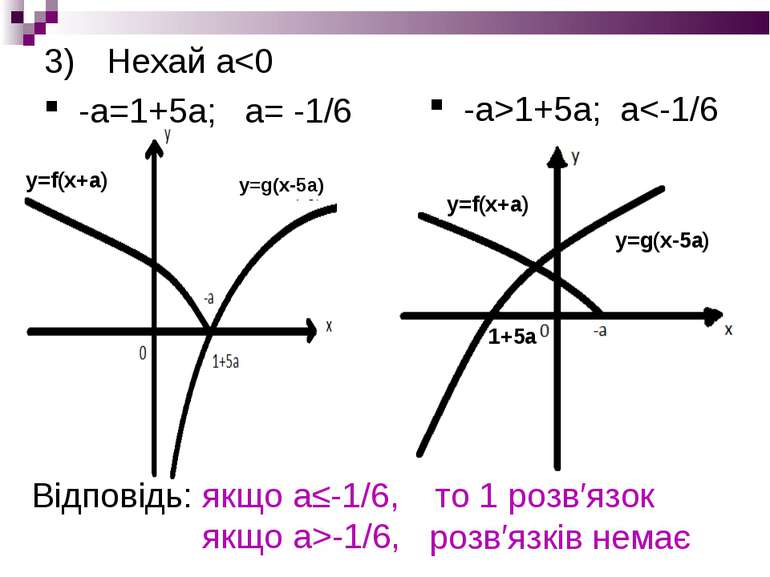
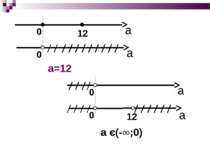
Граничне значення а=0 2lg(x+3)=lg0 – не має змісту Отже: рівняння 2lg(x+3)=lgах або (x+3)2=ах має один корінь Якщо а=0, то рівняння розв′язку не має Відповідь: а є (-∞;0) та а=12

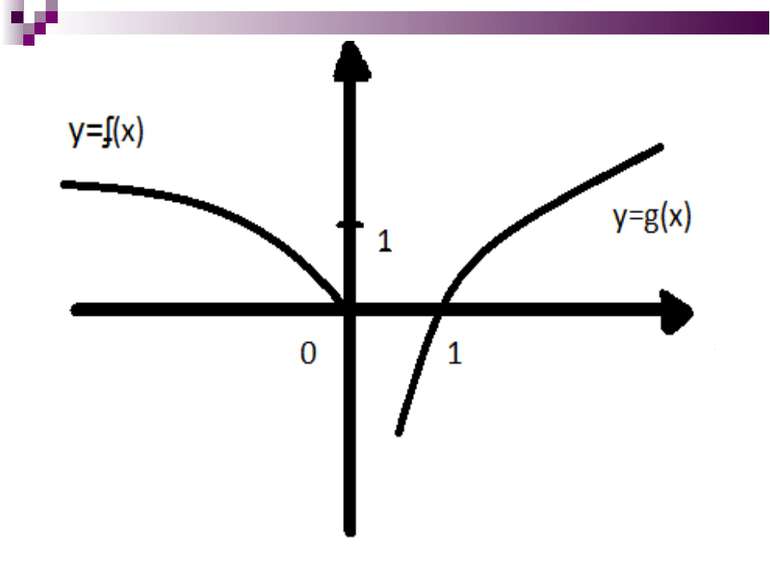
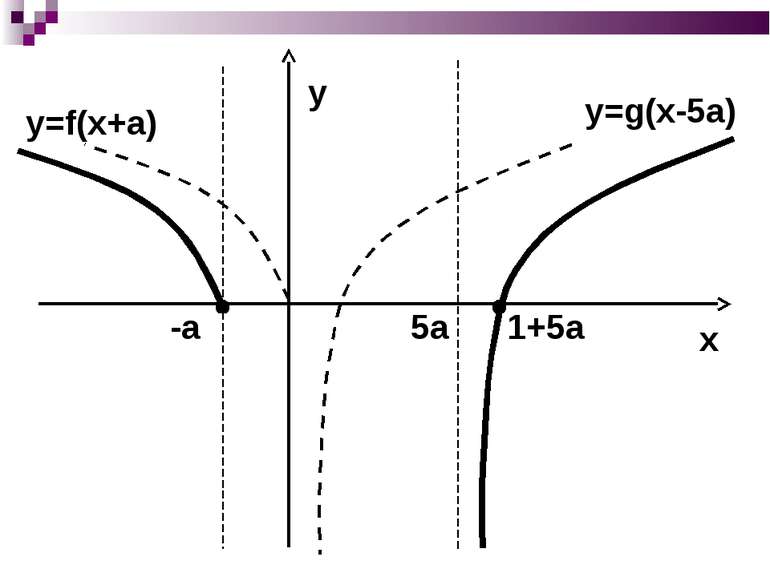
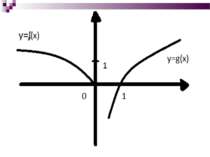
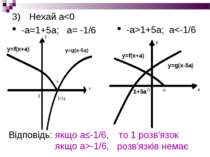
Завдання№4 Знайти кількість коренів рівняння – log5(x-5a)=0 в залежності від значення а Нехай а=0, Розвязання: тоді y=f(х)= і y=g(x)=log5x D(f): -x≥0; x≤0 D(g): x>0

Нехай а>0, тоді у=ʄ(х)= =0 -х-а=0, або х=-а у=g(x)=log5(x-5a) х – 5а = 1, або х = 1+5а

Нехай а1+5а; а-1/6, то 1 розв′язок розв′язків немає

Підсумки заняття Згадали: Розв'язання логарифмічних рівнянь і нерівностей Графічний метод розв'язання рівнянь Умови визначення кількості коренів квадратного рівняння Умови залежності значення квадратного тричлена від знака дискримінанта і старшого коефіцієнта Як досліджувати граничні значення параметрів і правильно записувати відповіді

БАЖАЮ УСПІХІВ В ПОДАЛЬШОМУ НАВЧАННІ