Презентація на тему:
Координатна площина

Координатна площина 6 клас Математика

Мета уроку: навчити учнів будувати точки по заданим координатам і визначати координати точки, зображеній на координатной площині. Завдання уроку: навчити вільно орієнтуватися на координатній площині; виконувати геометричні побудови; активізувати увагу учнів з допомогою мультимедійних засобів; розвивати творчі здібності та інтерес до математики.

Визначити місцезнаходження об'єкта – означає надати таку інформацію, за якою його можна знайти однозначно: - номер квартири і будинку; - широту і довготу на географічній карті; - номер ряду і місця в кінотеатрі.

Системи координат оточують нас всюди : - З допомогою координатної сітки пілоти, моряки визначають місцезнаходження об'єктів ; - використовуються на туристичних схемах для пошуку визначних місць або потрібної вулиці; - при астрономічних спостереженнях координатна сітка використовується для складання зоряних і географічних карт.

  Ті, хто в дитинстві грав в морський бій, також пам'ятають, що кожна клітинка на гральному полі визначалась двома координатами - буквою і цифрою. Те ж можна сказати і про гру в шахи. а в d с е f к l m n 1 2 3 4 5 6 7 9 10 8

Більш ніж за 100 років до н.е грецький вчений Гіппарх запропонував опоясати на карті земну кулю паралелями и меридіанами та ввести зараз добре відомі географічні координати: широту та довготу і позначити їх числами.

У II віці н.е. відомий древньогрецький астроном Клавдій Птоломей вже користувався довготою і широтою в якості географічних координат.

В ХIV столітті французький вчений Оресле по аналогії з географічними координатами створив координатну площину. Він розмістив на площині прямокутну сітку і назвав широтою і довготою те, що зараз ми називаємо абсцисою і ординатою. Терміни абсциса і ордината були введені в використання Лейбніцем в XVII столітті. Та основна роль в створенні методу координат належить французькому вченому Рене Декарту.

Рене Декарт (1596-1650) французький філософ і математик, ввів поняття координатної площини, тому її часто називають декартовою системою координат.

Терміни «абсциса» , «ордината», «координати» першим почав використовувати в кінці 17 століття Готфрід Вільгельм Лейбніц.

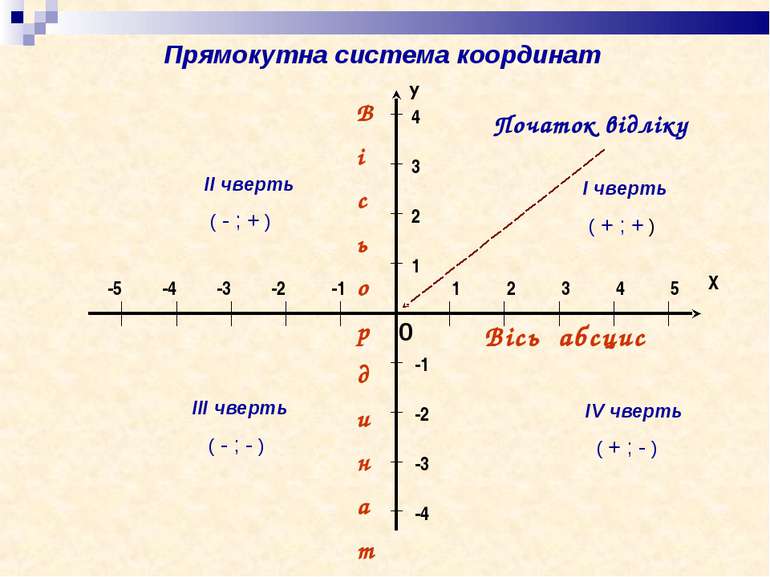
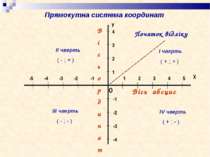
Вісь абсцис В і с ь о р д и н а т 0 Початок відліку ІІ чверть ( - ; + ) І чверть ( + ; + ) ІІІ чверть ( - ; - ) ІV чверть ( + ; - ) Прямокутна система координат

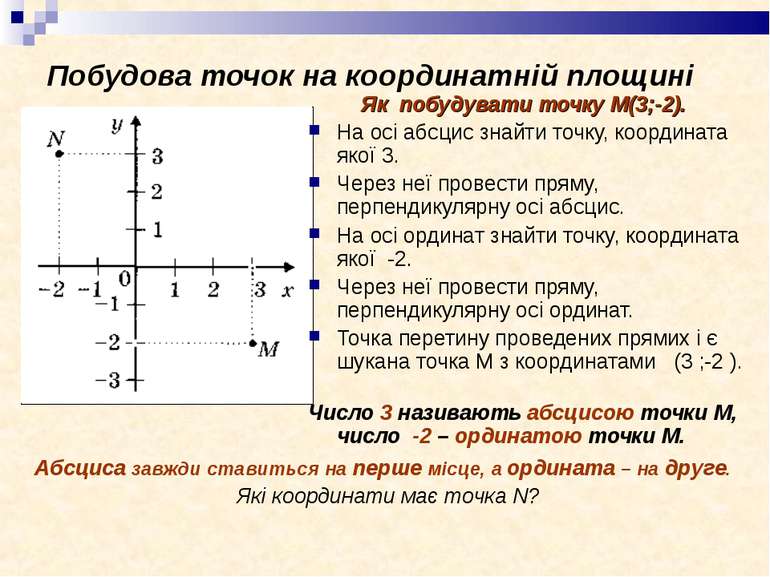
Побудова точок на координатній площині Як побудувати точку М(3;-2). На осі абсцис знайти точку, координата якої 3. Через неї провести пряму, перпендикулярну осі абсцис. На осі ординат знайти точку, координата якої -2. Через неї провести пряму, перпендикулярну осі ординат. Точка перетину проведених прямих і є шукана точка М з координатами (3 ;-2 ). Число 3 називають абсцисою точки М, число -2 – ординатою точки М. Абсциса завжди ставиться на перше місце, а ордината – на друге. Які координати має точка N?

Знайдіть координати точок, зображених на малюнку R А В С G Е F D S K H R Q M

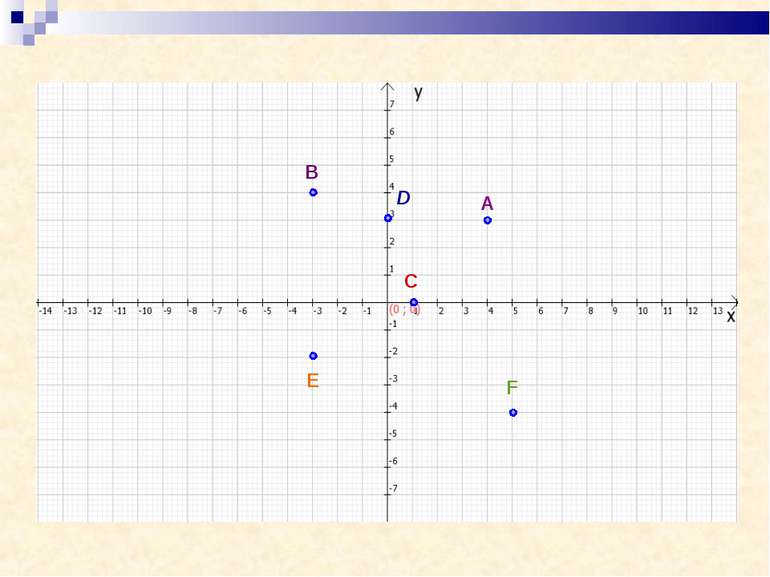
Завдання Накресліть в зошиті координатну площину, взявши за одиничний відрізок 1 см. Позначте точки: А(4;3); В (-3;4); С(1;0); D(0;3); E(-3;-2); F(5;-4).

А В С D Е F

Завдання Дано координати трьох вершин прямокутника ABCD: А(-3;-1),В(-3;3) i D(5;-l). 1) Накресліть цей прямокутник. 2) Знайдіть координати вершини С. 3) Обчисліть площу і периметр прямокутника, вважаючи, що довжина одиничного відрізка координатних осей дорівнює 1 см.

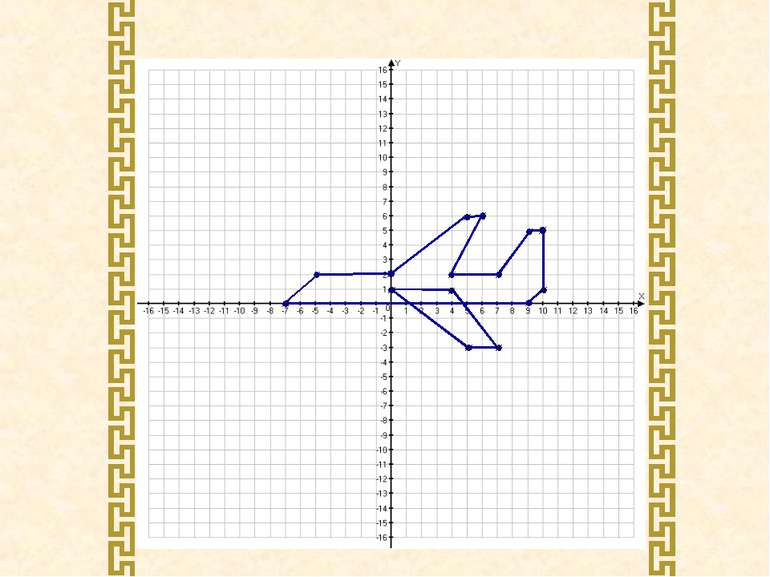
Накресліть на координатній площині дві замкнені ламані, послідовними вершинами якої є точки з координатами: І. (-7; 0), (-5; 2), (0; 2), (5; 6), (6; 6), (4; 2) (7; 2), (9; 5), (10; 5),(10; 1), (9; 0), (-7; 0). ІІ. (0;1), (4; 1), (7; -3), (5; -3), (0; 2).

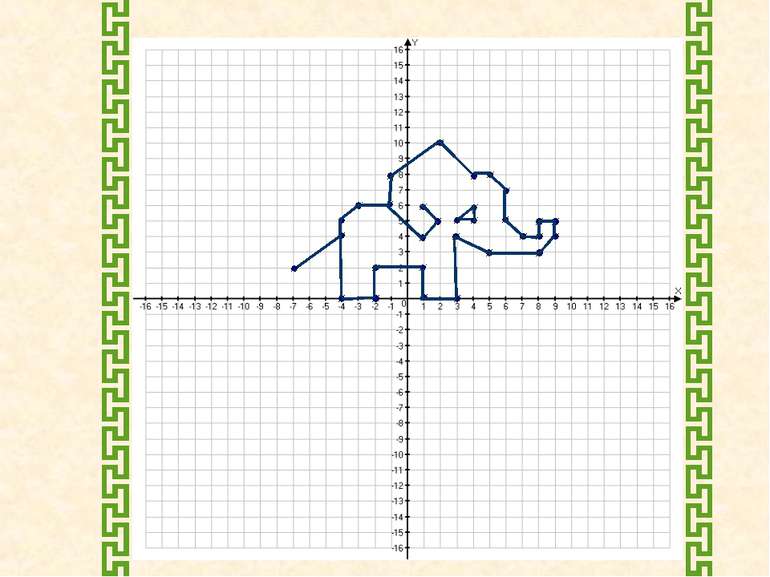
Накресліть на координатній площині дві замкнені ламані, послідовними вершинами якої є точки з координатами: І. (-4;0), (-1;5), (3;6), (-1;6), (-1;8), (2;10), (4;8), (5;8), (6;7),(6;5), (7;4), (8;4), (8;5), (9;5), (9;4), (8;3), (5;3), (3;4), (3;0),(1;0), (1;2), (-2;2), (-2;0), (-4;0). ІІ. (-1;6),(1;4),(2;5),(1;6). ІІІ. (3;5),(4;6),(5;5). IV. (-4;4),(-7;2).

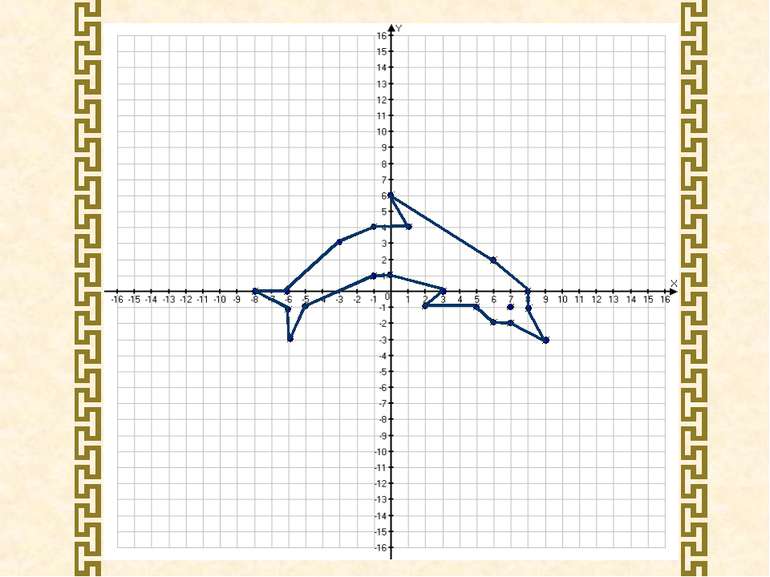
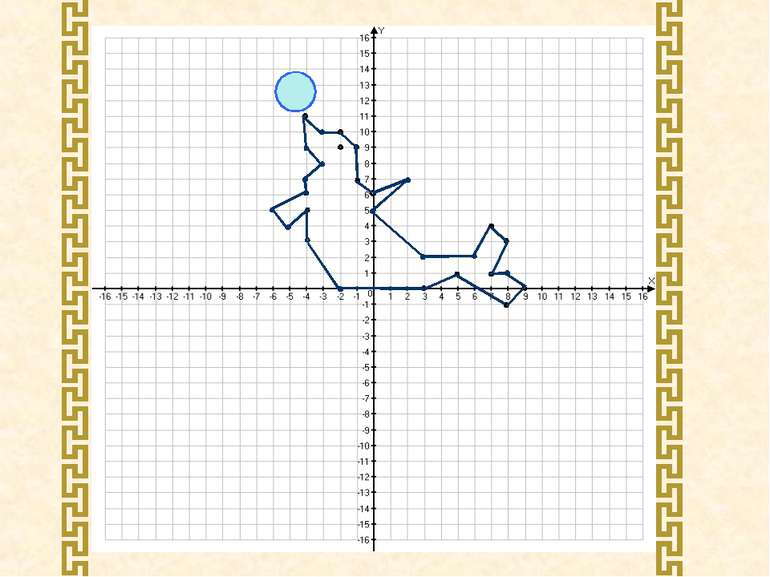
Накресліть на координатній площині замкнену ламану, послідовними вершинами якої є точки з координатами: (8; 0), (6; 2), (0; 6), (1; 4), (-1; 4), (-3; 3), (-6; 0), (-8; 0), (-6; -1), (-6; -3), (-5; -1), (-1; 1), (0; 1), (3; 0), (2; -1), (5; -1), (6; -2), (7; -2), (9; -3), (8; -1), (8; 0). Позначте точку (7; -1).

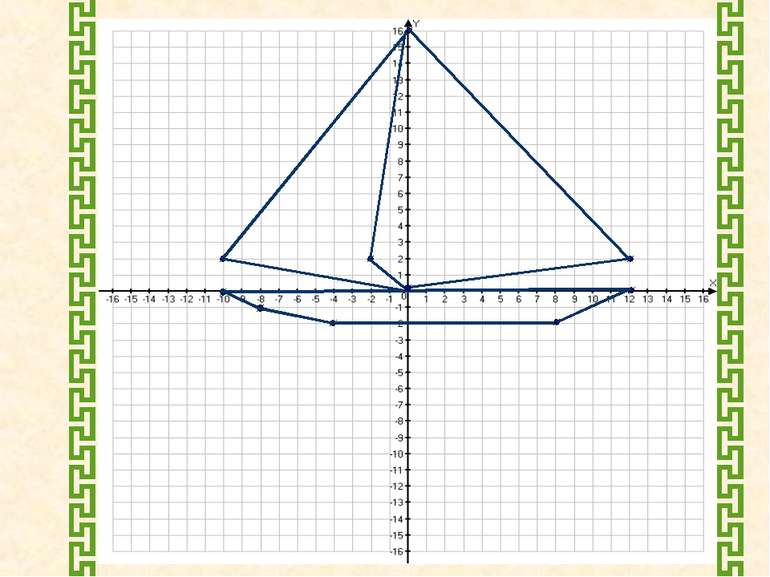
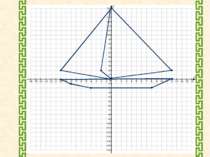
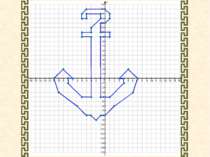
Накресліть на координатній площині замкнену ламану, послідовними вершинами якої є точки з координатами: І. (-10; 0), (-8; -1), (-4; -2), (8; -2), (12; 0), (-10; 0). ІІ. (0; 16), (12; 2), (0; 0), (-10; 2), (0; 16). ІІІ. (0; 16), (-2;2), (0; 0), (0; 16).

Накресліть на координатній площині замкнену ламану, послідовними вершинами якої є точки з координатами: (-2;0), (3;0) (5;1), (8;-1), (9;0), (8;1), (7;1), (8;3), (7;4), (6;2), (3;2), (0;5), (2;7), (7;0), (-1;7), (-1;9), (-2;10), (-3;10), (-4;11), (-4;9), (-3;8), (-4;7), (-4;6), (-6;5), (-5;4), (-4;5), (-4;3), (-2;0). Точка (-2;9).

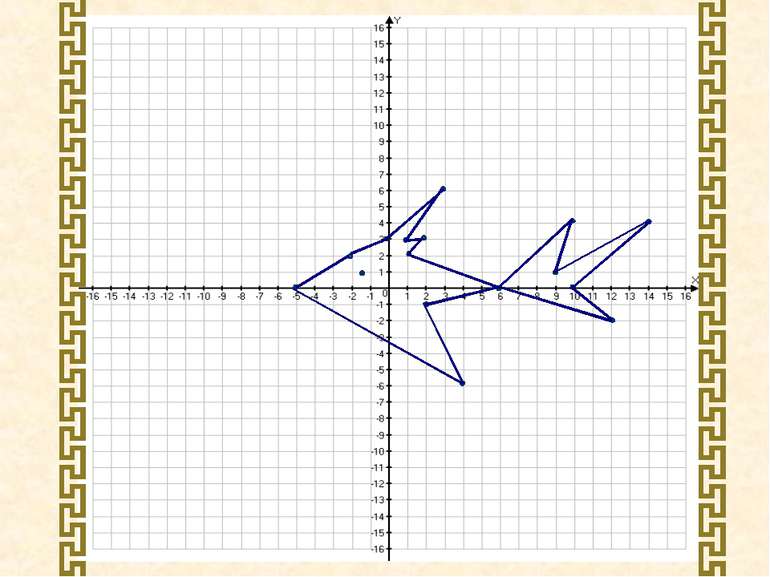
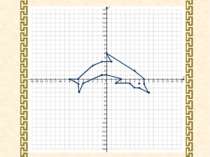
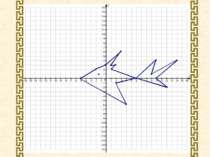
Накресліть на координатній площині замкнену ламану, послідовними вершинами якої є точки з координатами: (-5;0), (4;-6), (2;-1), (6;0), (12;-2), (10;0), (14;4), (9;1), (10;4), (6;0), (1;2), (2;3), (1;3), (3;6), (0;3), (-2;2), (-5;0). Точка (-1,5;1).

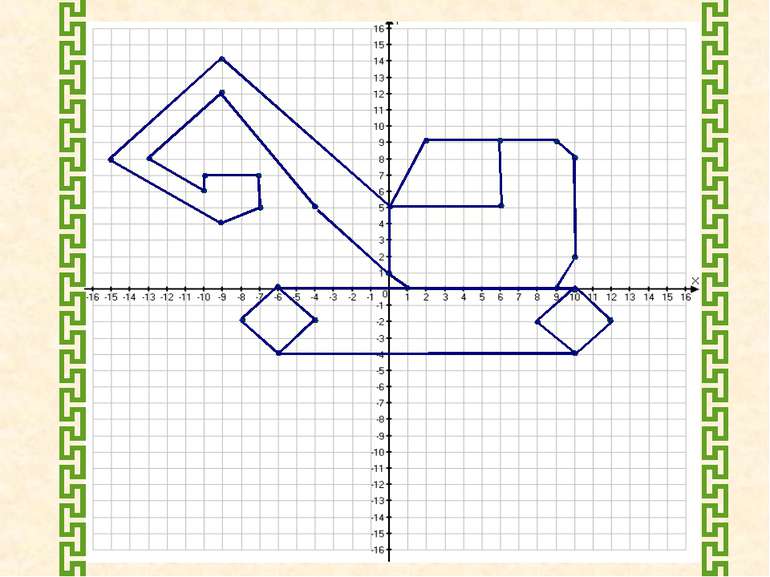
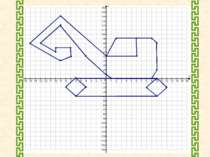
Накресліть на координатній площині замкнену ламану, послідовними вершинами якої є точки з координатами: (-6;0),(-8;-2),(-6;-4),(-4;-2),(-6;0). (10;-4),(12;-2);(10;0),(8;-2),(10;-4). З'єднати точки (-6;-4) і (10;-4), (10;0) і (-6;0). (9;0),(10;2),(10;8), (9;3); (2;9); (0;5); (6;5); (6;9); (0;1); (1;0). (0;5); (-9;14); (-15;8); (-9;4); (-7;5); (-7;7); (-10;7); (-10;6); (-13;8); (-9;12); (-4;5); (0;1).

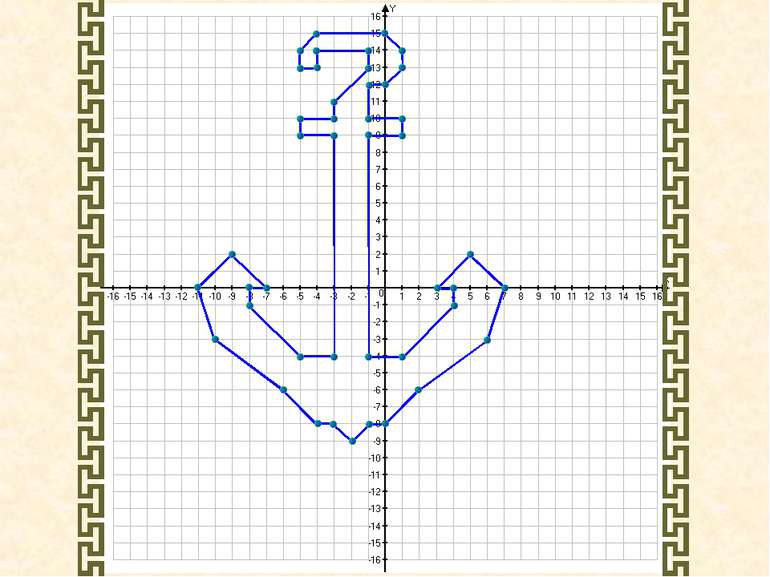
Накресліть на координатній площині замкнену ламану, послідовними вершинами якої є точки з координатами: (3;0); (5;2); (7;0); (6;-3); (2;-6); (0;-8); (-1;-8) (-2;-9); (-3;-8); (-4;-8); (-6;-6); (-10;-3); (-11;0); (-9;2) (-7;0); (-8;0); (-8;-1); (-5;-4); (-3;-4); (-3;9); (-5;9); (-5;10); (-3;10); (-3;11); (-1;13); (-1;14); (-4;14); (-4;13); (-5;13); (-5;14); (-4;15); (0;15); (1;14); (1;13) (0;12); (-1;12); (-1;10); (1;10); (1;9); (-1;9); (-1;-4) (1;-4); (4;-1); (4;0); (3;0)

Дякую за співпрацю і до зустрічі !