Презентація на тему:
Додавання та віднімання раціональних чисел. Розв’язування вправ

Додавання та віднімання раціональних чисел. Розв’язування вправ 6 клас Вчитель математики Андрієнко І.О.

Мета : встановити зв'язок між додаванням і відніманням раціональних чисел; удосконалювати вміння застосування правил додавання додатних і від’ємних чисел, віднімання раціональних чисел та виробити навички застосування їх при виконанні вправ; розвивати логічне мислення, пізнавальну активність учнів, творчі здібності та обчислювальні навички, інтересу до навчання; виховання дисциплінованості, самостійності, культури математичного запису.

Натуральні числа, протилежні їм числа і Число нуль називаються …… (Цілими ) Нам ці числа вже відомі Цілі і дробові, Від’ємні і додатні, І звуться вони ….. (раціональні). Нам ці числа треба знати, Щоб від двох п’ятьсот відняти. З ними дія додавання – Це суцільне здивування. Все одно вони приємні – Числа на ім’я .... (від’ємні) Загадкове, нам знайоме, В ньому є щось невідоме, Його треба розв’язати, Тобто корінь відшукати. Кожен легко, без вагання Відповість, що це - …… (рівняння). Хто швидше? Знайдіть в таблиці послідовно числа від 26 до 50 37 30 47 46 44 42 33 27 36 39 34 48 50 31 43 28 41 38 49 26 45 32 29 40 35

Нам ці числа треба знати, Щоб від двох п’ятсот відняти. З ними дія додавання – Це суспільне здивування. Все одно вони приємні, Числа на ім’я … Відгадайте загадку Від’ємні

Які числа називаються додатними? Які числа називаються від’ємними? Яке число не є ні від’ємним, ні додатним? Які числа називаються протилежними? Яке число не має протилежного? Які числа називаються натуральними? Які числа називаються цілими? Які числа називаються раціональними? Що називають модулем числа? Що означає порівняти два числа? Як порівняти два раціональних числа? Як порівняти два від’ємних числа?

Яке число має більший модуль? Яке число більше? -4 і 6; -5 і -12; 3) 3,8 і 4,6; 4) -2,4 і 5,1; 5) -14 і 0,1; 6) -0,03 і -0,3. 1.

У яку точку перейде точка М(-3), якщо перемістити її: на 7 одиниць; 2. -3 М 0 на -7 одиниць; +7 4 на 3 одиниці; +3 на -3 одиниці. +(-7) -10 +(-3) -6

3. -7,86; 2) 0,16; 3) -0,08; 4) -3. Між якими сусідніми цілими числами лежить число: -7,86 -8 -7 0,16 0 1 -0,08 0 -1 -3 -2 -4

Мозковий штурм Як додати два від’ємних числа? Чому дорівнює сума двох протилежних чисел? Як знайти суму додатного і від’ємного числа? Як від одного раціонального числа відняти друге?

Замість зірочки поставте «+» або «-» *4,8 – (*8,9) = - 4,1, *7 – (*1) = - 6, 4 * ( - 11) = 15, 12 * ( -16) = 28, *1,5 – (* 1,5) = 0, *2,5 – ( * 2,5) = -5, – 3,2 *2,4 = - 5,6, – 12 * ( - 8) = - 4. 4,8 – 8,9 = - 4,1, - 7 – (- 1) = - 6, 4 - ( - 11) = 15, 12 - ( -16) = 28, - 1,5 – (- 1,5) = 0, -2,5 – 2,5 = -5, – 3,2 - 2,4 = - 5,6, – 12 - ( - 8) = - 4.

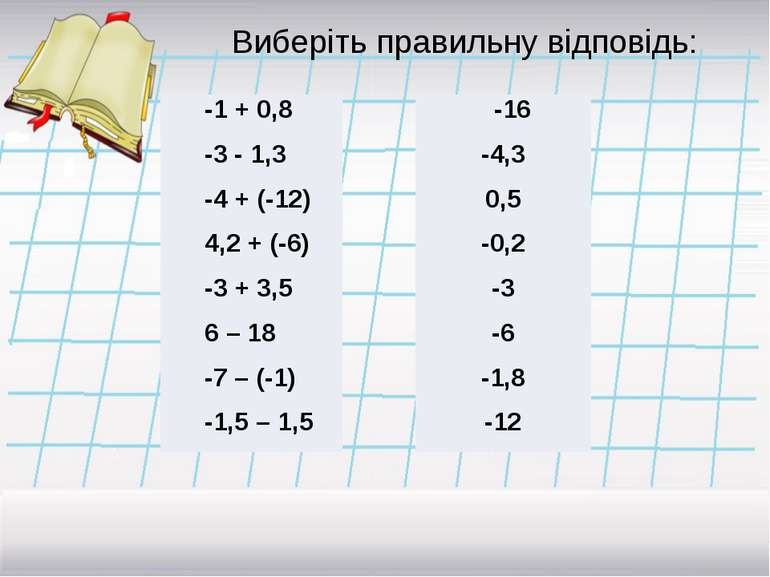
Виберіть правильну відповідь: -1 + 0,8 -3-1,3 -4 + (-12) 4,2 + (-6) -3 + 3,5 6 – 18 -7 – (-1) -1,5 – 1,5 -16 -4,3 0,5 -0,2 -3 -6 -1,8 -12

№ 1048 Якщо а = -3,1; в = 5,7; с = -4,8. а+в+с Іа+в+сІ ІаІ+ІвІ+ІсІ =-3,1 + 5,7 + (-4,8) = -2,2 =І -3,1 + 5,7 + (-4,8)І =2,2 Обчисліть =І -3,1 + 5,7 + (-4,8)І =2,2

Розв’яжіть рівняння № 1057(а,в) І 4 – х І =3; 4 – х = 3 або 4 – х = -3 х = 1. х = 7. Відповідь: 1 і 7. 3 + х = 5 або 3 + х = -5 х = 2. х = -8. Відповідь: -8 і 2. в) 6 + І 4 – х І = 9; а) І 3+ хІ = 5;

Офтальмопауза: Переведіть погляд з червоного круга на синій, з синього на зелений, з зеленого на жовтий. А тепер повторіть все в зворотньому порядку.

ребуси За

ЗАДАЧА 1 Гілки смородини витримують температуру до -50С, а після загартування вони можуть витримувати температуру, на 580С нижчу. Яку температуру можуть витримати гілки смородини після загартування? Відповідь: -630С.

ЗАДАЧА 2 Коли мороз сягає -400С, температура песця - +380С, а білої куріпки - +430С. На скільки температура тіл песця і куріпки вищі від температури повітря?   Відповідь: 780С; 830С.

ЗАДАЧА 3 Джмелі витримують температуру до -7,80С, оси – вищу від цієї на 1,40С, а бджоли – нижчу від цієї на 1,40С. Яку температуру витримують бджоли й оси? Відповідь: -6,40С; -9,20С.

1. Яке з поданих чисел є від’ємним? А. 9; Б. -0,9; В. ; Г. 0,9. 2. Які з поданих пар чисел є протилежними? А. 7 і ; Б. 7 і ; В. 7 і 0,7; Г. 7 і -7. 3. Модулем числа 8 є число … А. -8; Б. 8; В. ; Г. . 4. Модулем числа -18 є число … А. ; Б. -18; В. 18; Г. . 5. Яке з поданих чисел є найбільшим? А. -30; Б. -90; В. 90; Г. 30. 6. У якому з поданих прикладів під час дії додавання чисел їх модулі додають? А. -8 + 15; Б. -18 + (-19); В. 14 + (-15); Г. 17 + (-12). 7. У якому з поданих прикладів під час додавання чисел їх модулі віднімають? А. -12 + (-8); Б. -3 + (-16); В. -17 + 5; Г. -7 + (-12) 8. Яка з поданих сум є додатним числом? А. -1 + (-17); Б. 9 + (-17); В. -9 + 17; Г. -5 + (-3). 9. Яке з поданих чисел є сумою чисел -19 + (-5)? А. 24; Б. -24; В. 14; Г. -14. 10. Яке з поданих чисел є кореням рівняння х – 2,3 = -5,8? А. 3,5; Б. -3,5; В. 8,1; Г. -8,1. 11. Яке з поданих чисел є коренем рівняння х – (-3,4) = 5,17? А. -1,7; Б. 1,7; В. 8,5; Г. -8,5. Б. -0,9 Г. 7і -7 Б. 8 В. 18 В. 90 Б В В Б. -24 Б. -3,5 Б. 1,7 Б Р А Х М А Г У П Т А

Брахмагупта індійський математик, який жив у VII столітті. Одним з перших він почав використовувати додатні та від’ємні числа. Додатні числа він назвав «майно», від’ємні – «борг». «Сумма двух имуществ есть имущество» «Сумма двух долгов есть долг» «Сумма имущества и долга равна их разности» ».