Презентація на тему:
Тестовi норми

Тестові норми

Питання до лекції 1. Поняття “тестова норма”. Параметри норм. 2. Стандартні тестові норми. 3. Квантільна стандартизація 4. Види норм. 5. Правила розробки тестових норм. 6. Рекомендації щодо розробки тестових норм.

1. Поняття “тестова норма”. Параметри норм. Основою наукової інтерпретації тестових випробувань є наявність психологічно і статистично обгрунтованих норм. Тестові норми являють собою емпірично встановлені на базі репрезентативної вибірки усереднені кількісні дані про результати виконання тесту.

В складі тестових норм виділяють: 1) середні оцінки продуктивності або вираженості ознаки; 2) міри різноманітності індивідуальних оцінок відносно середніх

1.Середні оцінки продуктивності або вираженості ознаки Для визначення середніх або найбільш типових значень сукупності тестових балів використовуються показники центру розподілу (міри центральної тенденції). Основні з них — мода, медіана, середньоарифметичне значення. 1) Мода (Мо) – це таке значення в множині спостережень, яке зустрічається найчастіше. Наприклад: сукупність значень: 2, 6, 6, 8, 9, 9, 9, 10. Модою являється 9, тому, що воно зустрічається частіше будь-якого значення.

2) Медіана (Ме) - це значення, яке поділяє упорядковану множину даних навпіл (одна половина (50%) значень буде більше медіани, друга половина(50%) – менше). 1) Якщо дані містять непарну кількість різних значень, наприклад: 11, 13, 18, 19, 20, то медіаною є середнє значення для випадку, коли вони упорядковані, тобто Мd = 18. 2) Якщо дані містять парну кількість різних значень, наприклад: 4, 9, 13, 14, то медіаною буде число (точка на числовій шкалі), що лежить посередині між центральними значеннями, коли вони упорядковані, тобто Мd = (9+13):2=11.

3) Середньоарифметичне значення (М) - частка від ділення суми чисел на їх кількість Σ хі х1 + х2 + х3 +…. хn n , чи n Найчастіше для побудови норм для тесту використовують середньоарифметичне значення результатів тестових випробувань. Х Х

2. Міри різноманітності індивідуальних оцінок відносно середніх (розмах, дисперсія, середньоквадратичне відхилення) 1) Розмах – виміряє на числовій шкалі відстань, в межах якої змінюються оцінки. Наприклад: 0, 2, 3, 5, 8 розмах (8 – 0) = 8

2) Дисперсія – міра мінливості даних відносно середнього значення по виборці. (При підрахуванні використовується кожна оцінка множини) 2 Σ (х – хі) n – 1 Дисперсія – це ширина розподілу, тобто ступень відхилення даних від середнього. Чим менше дисперсія, тим менше розкид окремих значень, - тим вище точність виміру. σ 2

3) Середньоквадратичне відхилення від середнього значення по виборці Σ (х – хі) n – 1 Серед мір різноманітності індивідуальних оцінок найчастіше для побудови норм для тесту використовують середньоквадратичне (стандартне) відхилення. σ 2

Отже, основними параметрами, які має тестова норма, являються виборочна середня (М) і середнньоквадратичне відхилення (σ). Тоді, нормою вважається діапазон значень (σ – М + σ) Але, для того, щоб такі результати вважалися нормою, група, на якої проводиться тест, повинна бути сформованою певним чином. Існують правила формування такої групи досліджуваних, яка має назву вибірка стандартизації - це вибірка, на якої встановлюється норма.

Правила формування вибірки стандартизації: вибірка стандартизації повинна складатися з респондентів, на яких орієнтований даний тест, тобто якщо створюваний тест орієнтований на дітей (наприклад, тест Векслера або ШТРР), то і стандартизація повинна відбуватися на дітях заданого віку; вибірка стандартизації повинна бути репрезентативною, тобто бути зменшеною моделлю генеральної сукупності по таких параметрах, як вік, стать, професія, національність тощо. Кількість досліджуваних (N) повинно бути достатньо велике. Адже передбачається, що ми поширюємо дану норму на решти всіх осіб з аналогічними соціально-демографічними характеристиками - на генеральну сукупність. Для того, щоб визначити норми, дослідник повинен провести тест на цієї виборці стандартизації і отримати результати. 25

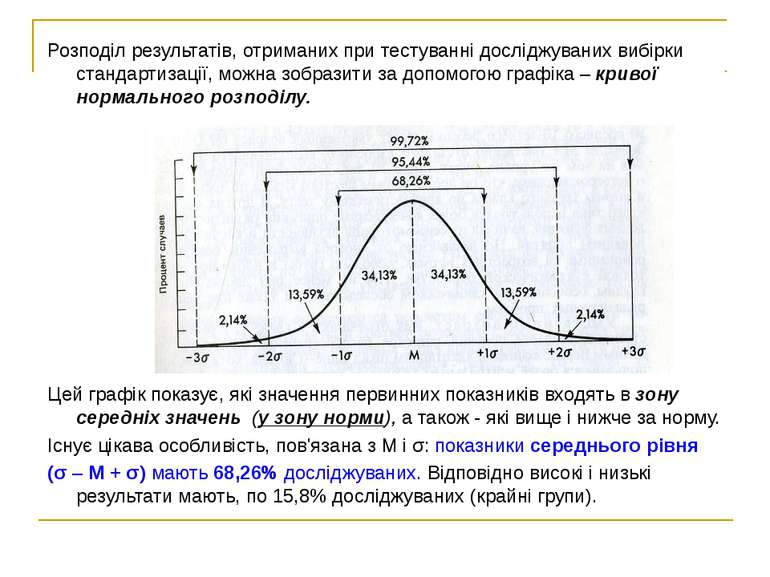
Розподіл результатів, отриманих при тестуванні досліджуваних вибірки стандартизації, можна зобразити за допомогою графіка – кривої нормального розподілу. Цей графік показує, які значення первинних показників входять в зону середніх значень (у зону норми), а також - які вище і нижче за норму. Існує цікава особливість, пов'язана з М і σ: показники середнього рівня (σ – М + σ) мають 68,26% досліджуваних. Відповідно високі і низькі результати мають, по 15,8% досліджуваних (крайні групи).

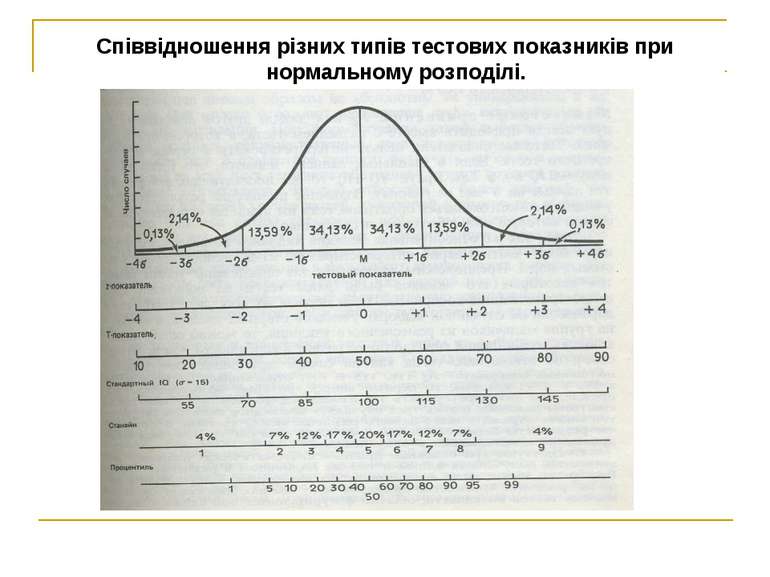
2. Стандартні тестові норми В керівництві до тесту можна зустріти вираження норми не у вигляді сирих балів (первинних показників), а у вигляді стандартних (похідних) показників. Переклад в стандартні (похідні) показники робиться для того, щоб результати, отримані по різних тестах, можна було порівнювати між собою. Сирі значення по різних тестах не можна порівнювати між собою унаслідок того, що тести мають різну внутрішню будову. Наприклад, IQ, отриманий за допомогою тесту Векслера, не можна порівнювати з IQ, отриманим за допомогою тесту Амтхауера або Равена, оскільки ці тести досліджують різні особливості інтелекту і IQ, як сумарний показник по субтестах, складається з показників різних по будові і змісту субтестів.

Нормами до тесту, що виражені у вигляді стандартних (похідних) показників являються Т-бали, стени, стандартні IQ, станайни тощо. Вони є результатами стандартизації (лінійного перетворення масштабу шкали у вигляд, зручний для практичного використання). Так, для шкали Т-балів М = 50; σ = 10; для шкали IQ М = 100; σ = 15 (шкала Векслера). Рис.

Співвідношення різних типів тестових показників при нормальному розподілі.

Ще одним дуже зручним, найефективнішим методом описання груп даних є квантільна стандартизація, за допомогою якої проводиться інтерпретація в вигляді полярних психологічних характеристик особистості, інтелекту, групової поведінки тощо.

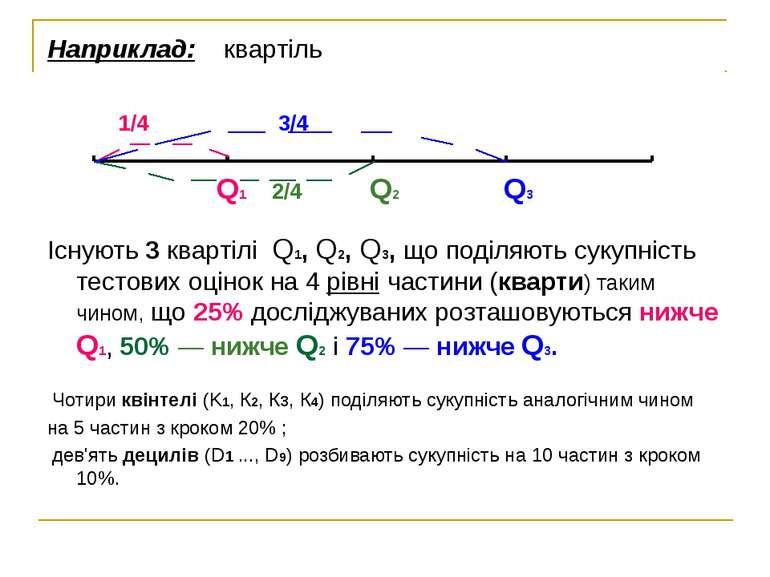
3. Квантільна стандартизація Квантіль – точка на числовій шкалі, яка поділяє сукупність тестових оцінок на групи з відповідними пропорціями в кожній з них. Квантіль – це загальне поняття, процентіль дециль його приклади (різновиди) квінтель квартіль Квартіль (Q) – поділяє сукупність даних на 4 рівні частини Квінтель (К) – поділяє сукупність на 5 частин Дециль (D) – на 10 частин Процентіль (Р) – на 100 частин

Наприклад: квартіль 1/4 3/4 Q1 2/4 Q2 Q3 Існують 3 квартілі Q1, Q2, Q3, що поділяють сукупність тестових оцінок на 4 рівні частини (кварти) таким чином, що 25% досліджуваних розташовуються нижче Q1, 50% — нижче Q2 і 75% — нижче Q3. Чотири квінтелі (K1, К2, Кз, К4) поділяють сукупність аналогічним чином на 5 частин з кроком 20% ; дев'ять децилів (D1 ..., D9) розбивають сукупність на 10 частин з кроком 10%.

Тест Равена Якісна характеристика рівня інтелекту згідно набраних процентілів децилі

Норми інтелекту: 140 – дуже високий інтелект 120 – 140 – високий інтелект 110 – 120 – інтелект вище середнього 90 – 110 – середній інтелект 80 – 90 – інтелект нижче норми 70 – 80 – легке слабоумство 50 – 70 – дебільність 20 – 50 – імбецильність 0 – 20 – ідіотія

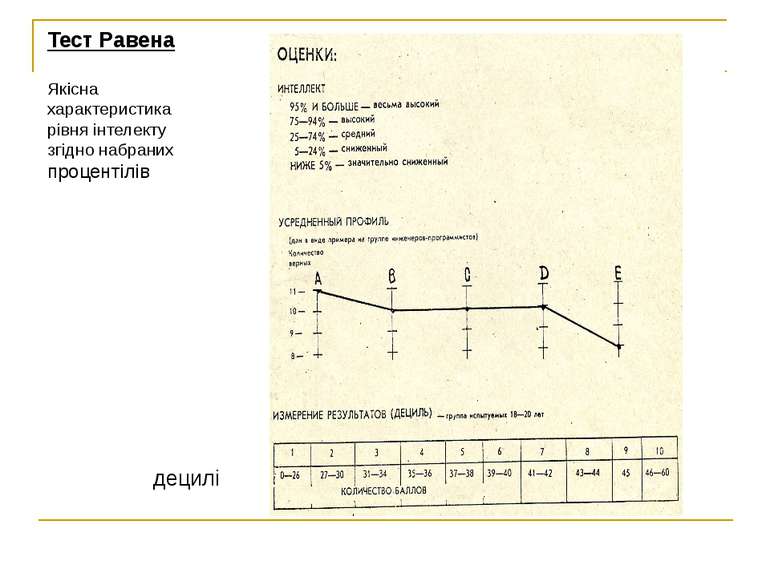
Тестові норми Векслера 130 балів і вище - дуже високий IQ - у 2,2% населення; 120-129 балів - високий IQ - у 6,7%; 110-119 балів - хороша норма - у 16,1% 90-109 балів - середній IQ - у 50%; 80-89 балів - погана норма - у 16,1% 70-79 балів - прикордонна зона - у 6,7%; 69 балів і нижче - розумовий дефект - у 2,2% населення; відсоток виявлення по вибірці 1700 осіб (від 16 до 64 років)

4. Види норм Існує ділення норм на універсальні, національні, професійні, шкільні, групові, локальні тощо. Універсальні норми встановлюються і застосовуються для широкого контингенту людей. Вони лише в малому ступені залежать від наявності або відсутності таких ознак, як стать, вік в діапазоні 17-60 років, статус тощо. Тому відмінності між групами, поділеними в відповідності з цими ознаками, малі і статистично незначущі. Прикладом таких норм є норми для тесту Бурдона (стійкість і розподіл уваги).

Національні норми розробляються для представників даної народності, нації, країни в цілому. Необхідність таких норм: диктується відмінностями в результатах застосування тесту навіть в країнах, що говорять на одній мові (наприклад, США і Англії), визначається конкретною культурою, моральними нормами і традиціями кожної нації. Професійні норми встановлюються на основі тестових батарей для різних професійних груп - механіків різного профілю, слюсарів різних спеціальностей, друкарок тощо.

Шкільні норми розробляються на основі тестів шкільних досягнень або тестів шкільних (академічних) здібностей. Вони встановлюються для кожного шкільного віку (східця) і діють на всій території країни. Групові норми розробляються для широких категорій людей, що відрізняються наявністю якої-небудь ознаки - віку, статі, географічного району, соціоекономічного статусу тощо. Наприклад, норми для набору тесту на інтелект Векслера обмежені тільки віковими ознаками.

Локальні норми встановлюються і застосовуються для вузьких категорій людей. Наприклад, норми допуску до іспиту в даному навчальному закладі, норми для відбору претендентів на відповідну роботу на підприємство або в організацію, тощо. .

5. Правила розробки тестових норм При розробці норм рекомендується враховувати наступне: 1) Норми встановлюються при розробці: нового тесту, при адаптації і редагуванні існуючого, при використанні тесту на вибірці, яка відмінна від стандартної по істотним для результатів тестування характеристикам (професії, освіти тощо).

2) Вибірка стандартизації при розробці норм повинна бути добре збалансованою за складом і чисельністю підгруп, що її складають. Наприклад: розробляючи загальнодержавні норми для діагностики рівня розвитку якого-небудь інтелектуального уміння, кількість досліджуваних різного віку, статі, рівня освіти, міських і сільських мешканців тощо, повинна бути пропорційною їх кількості в генеральної сукупності. 11 3) Всі відхилення від встановленої процедури нормування тестових результатів повинні спеціально обговорюватися в керівництвах до тесту (відхилення в процедурі стандартизації, в підборі досліджуваних, в їхній чисельності).

6. Рекомендації щодо розробки тестових норм При побудові тестових норм психолог повинен провести наступні дії: Сформувати стандартизовану вибірку з тієї популяції, на якій передбачається застосовувати тест. Провести на кожному досліджуваному вибірки тест в стислі терміни (щоб усунути розкид, викликаний зовнішніми подіями, що відбулися за час обстеження). Провести угрупування «сирих» балів з урахуванням вибраного інтервалу квантування. Побудувати розподіл частот тестових балів (для заданих інтервалів) у вигляді таблиці. Провести розрахунок середнього і стандартного відхилення.

Провести перевірку нормальності закону розподілу частот тестових балів (наприклад за допомогою критерію Колмогорова або інших потужних критеріїв). Якщо розподіл не підпорядковується нормальному закону, провести процентільну нормалізацію з перекладом у вибрану стандартну шкалу. Перевірити однорідність розподілу по відношенню до варіювання заданої ознаки популяції (стать, професія тощо) за допомогою критерію Колмогорова. Побудувати таблиці тестових норм (для кожного інтервалу «сирого» балу).

У керівництві тесту обов'язково повинна бути вказівка, де, як, на кому і коли встановлені його норми. Норми з часом змінюються – разом із зміною психологічного розвитку людей. Тому є емпірично встановлене правило, згідно якому як мінімум раз в п'ять років тестові норми – особливо для тестів інтелекту – підлягають перегляду. Процедура перегляду тестових норм типова: 1) визначається група людей, для яких передбачається застосовувати даний тест; 2) ця група розділяється на підгрупи, різні за соціально-демографічними характеристиками; 3) для кожної підгрупи підбирається і за допомогою цього тесту вивчається достатньо представницька вибірка людей; 4) шляхом усереднення отриманих показників визначається тестова норма для даної сукупності людей.