Презентація на тему:
Взаємне розміщення прямих у просторі

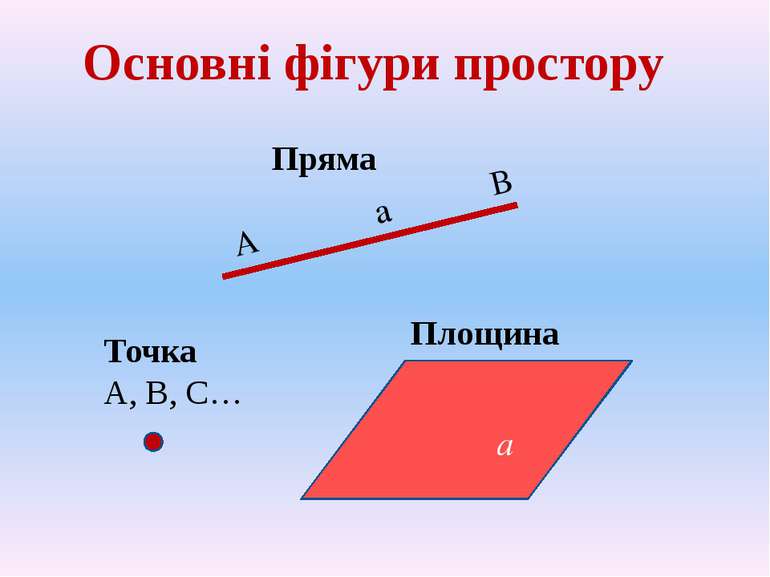
Взаємне розміщення прямих у просторі Підготувала вчитель математики Сербівської ЗОШ Трембовецька О.А.

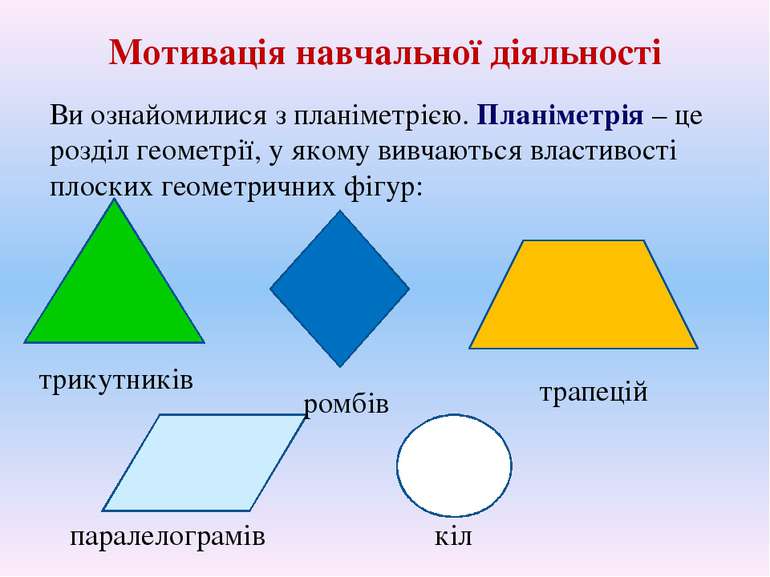
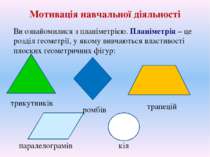
Мотивація навчальної діяльності Ви ознайомилися з планіметрією. Планіметрія – це розділ геометрії, у якому вивчаються властивості плоских геометричних фігур: трикутників паралелограмів кіл трапецій ромбів

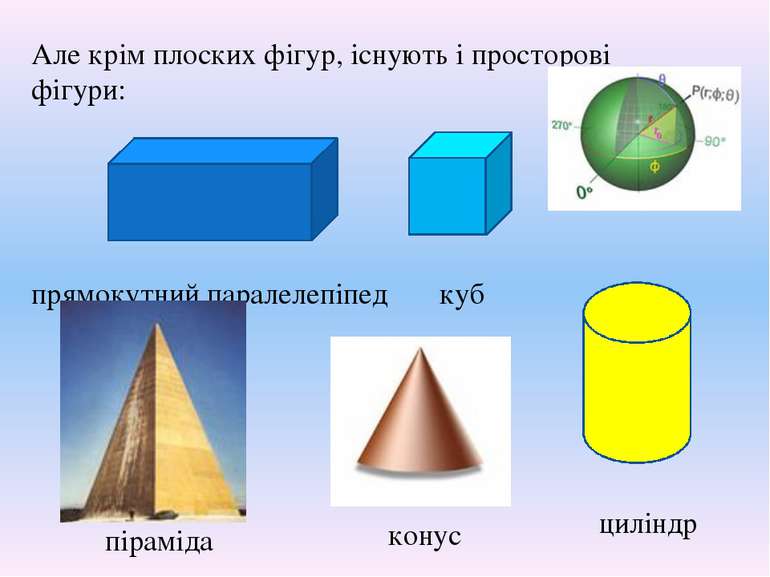
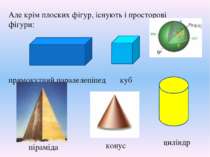
Але крім плоских фігур, існують і просторові фігури: прямокутний паралелепіпед куб куля піраміда циліндр конус

Багато предметів, що нас оточують, мають форму прямокутного паралелепіпеда:

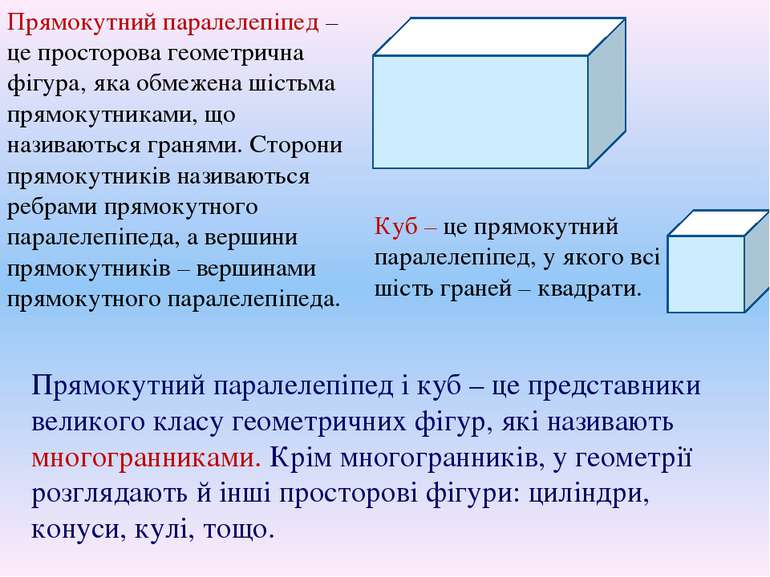
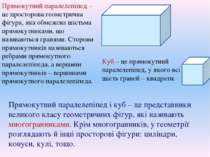
Прямокутний паралелепіпед – це просторова геометрична фігура, яка обмежена шістьма прямокутниками, що називаються гранями. Сторони прямокутників називаються ребрами прямокутного паралелепіпеда, а вершини прямокутників – вершинами прямокутного паралелепіпеда. Куб – це прямокутний паралелепіпед, у якого всі шість граней – квадрати. Прямокутний паралелепіпед і куб – це представники великого класу геометричних фігур, які називають многогранниками. Крім многогранників, у геометрії розглядають й інші просторові фігури: циліндри, конуси, кулі, тощо.

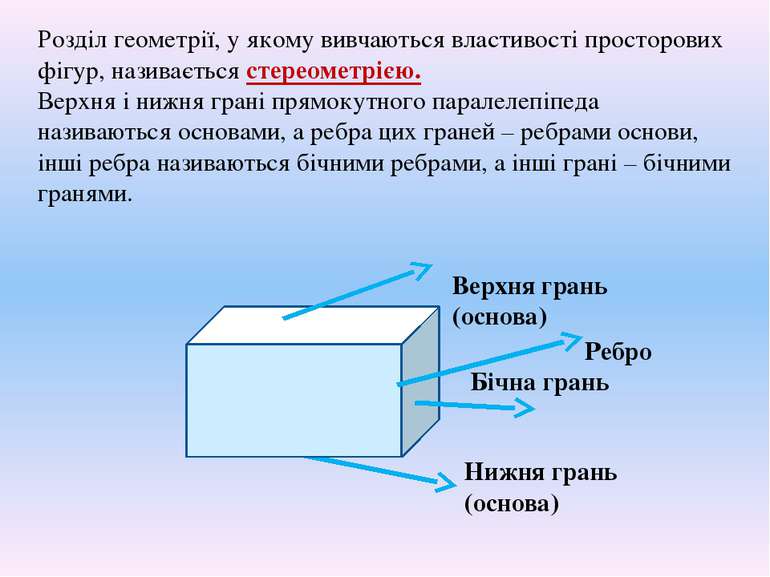
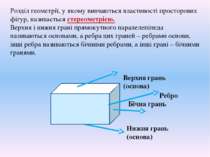
Розділ геометрії, у якому вивчаються властивості просторових фігур, називається стереометрією. Верхня і нижня грані прямокутного паралелепіпеда називаються основами, а ребра цих граней – ребрами основи, інші ребра називаються бічними ребрами, а інші грані – бічними гранями. Верхня грань (основа) Нижня грань (основа) Бічна грань Ребро

Основні фігури простору Точка А, В, С… Пряма Площина а А а В

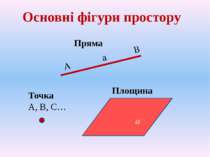
Основні аксіоми стереометрії Аксіома1. Яка б не була площина, існують точки, що належать цій площині, і точки, які їй не належать. Аксіома2. Якщо дві різні площини мають спільну точку, то вони перетинаються по прямій, що проходить через цю точку. Аксіома3. Якщо дві різні прямі мають спільну точку, то через них можна провести площину, і до того ж тільки одну.

Єдину площину можна провести: через дві прямі, що перетинаються; через дві паралельні прямі; через пряму і точку, яка не лежить на цій прямій; через три точки, що не лежать на одній прямій.

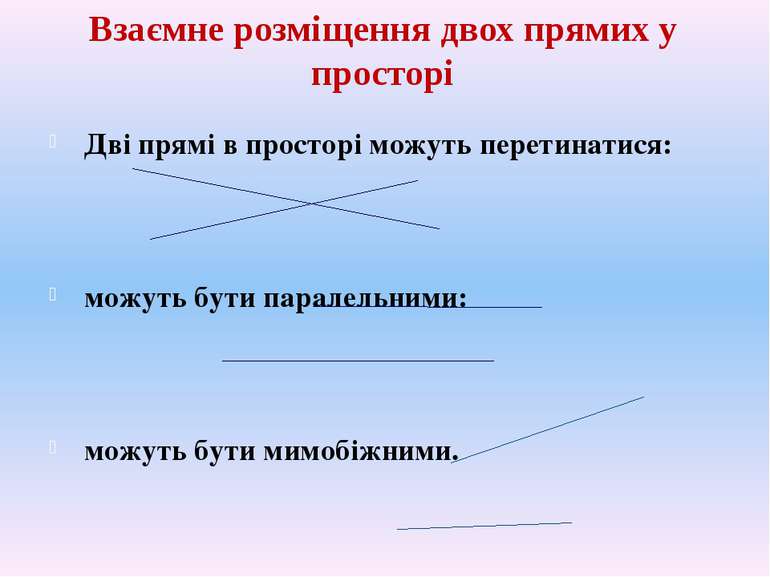
Взаємне розміщення двох прямих у просторі Дві прямі в просторі можуть перетинатися: можуть бути паралельними: можуть бути мимобіжними.

Дякую за увагу!