Презентація на тему:
Прямокутник та його властивості

ГЕОМЕТРІЯ 8 РОЗДІЛ 1 ЧОТИРИКУТНИКИ Підготувала Лисенко Галина Вікторівна вчитель математики Теклинської загальноосвітньої школи І-ІІ ступенів Смілянської районної ради Черкаської області ЧОТИРИКУТНИКИ. Паралелограм та його властивості Лисенко Г.В. Прямокутник та його властивості

ЗМІСТ Означення прямокутника Властивості прямокутника Ознаки прямокутника Площа прямокутника Периметр прямокутника Учимося доводити Працюємо самостійно Задачі на побудову Застосовуємо на практиці МЕТА. Систематизувати знання учнів про прямокутник та його властивості ; закріпити уміння і навички використання властивостей при розв’язуванні задач на доведення та побудову; продовжити вдосконалення навичок роботи у групах, показати практичне значення геометрії. розвивати логічне мислення, творчі здібності; вміння систематизувати та узагальнювати. виховувати самостійність, уважність, інтерес до предмету, повагу один до одного, ПРЯМОКУТНИК ТА ЙОГО ВЛАСТИВОСТІ ЧОТИРИКУТНИКИ. Прямокутник та його властивості Лисенко Г.В.

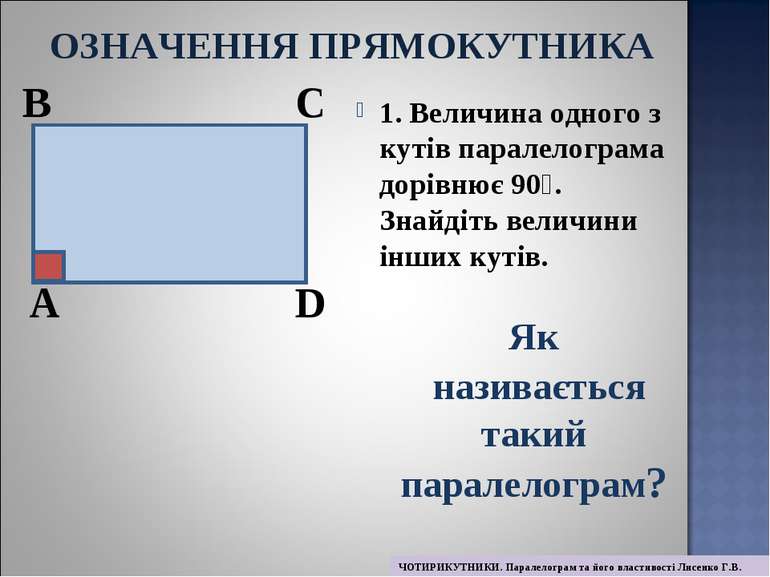
1. Величина одного з кутів паралелограма дорівнює 90⁰. Знайдіть величини інших кутів. A B C D Як називається такий паралелограм? ОЗНАЧЕННЯ ПРЯМОКУТНИКА ЧОТИРИКУТНИКИ. Паралелограм та його властивості Лисенко Г.В.

Прямокутник – це парале лограм, у якого всі кути прямі. A B C D Дати інші означення прямокутника ОЗНАЧЕННЯ ПРЯМОКУТНИКА ЧОТИРИКУТНИКИ. Паралелограм та його властивості Лисенко Г.В.

1.На шарнірній моделі паралелограма показати перетворення його в прямокутник. 2. Аналіз утвореної фігури. A B C D ЗВ’ЯЗОК ПРЯМОКУТНИКА З ПАРАЛЕЛОГРАМОМ ЧОТИРИКУТНИКИ. Паралелограм та його властивості Лисенко Г.В. 1. Чи можна назвати фігуру АВСD паралелограмом? 2. Які властивості паралелограма має ця фігура? 3. Які нові властивості має ця фігура?

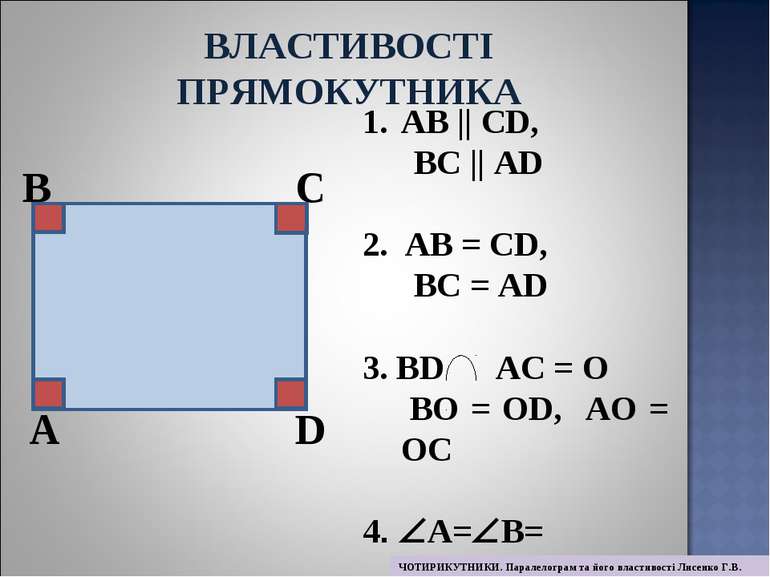
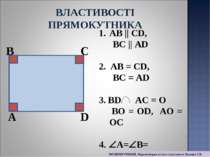
A B C D АВ || СD, ВC || АD 2. АВ = СD, ВС = АD 3. ВD АС = О ВО = ОD, АО = ОС 4. А= В= С= D=90° ВЛАСТИВОСТІ ПРЯМОКУТНИКА ЧОТИРИКУТНИКИ. Паралелограм та його властивості Лисенко Г.В.

A B C D Дано: АВСD – прямокутник Доведіть: ВD=АС Доведення: АВ=СD, 2. АD – спільний катет, отже АВD = DСА ВD = АС Діагоналі прямокутника рівні ВЛАСТИВІСТЬ ДІАГОНАЛЕЙ ЧОТИРИКУТНИКИ. Паралелограм та його властивості Лисенко Г.В.

C D Якщо для чотирикутника справедливе хоча б одне з наступних тверджень, то він прямокутник ОЗНАКИ ПРЯМОКУТНИКА ЧОТИРИКУТНИКИ. Паралелограм та його властивості Лисенко Г.В. Діагоналі рівні і точкою перетину діляться пополам. Дві сторони паралельні і кути, що прилягають до однієї з них , прямі. Дві протилежні сторони рівні і кути, що прилягають до однієї з них прямі. Перпендикуляри до сторін, що проходять через їх середини, є осями симетрії.

SABCD=AB·BC A B D ПЛОЩА прямокут- ника дорівнює добутку його сторін ПЛОЩА ПРЯМОКУТНИКА ЧОТИРИКУТНИКИ. Паралелограм та його властивості Лисенко Г.В.

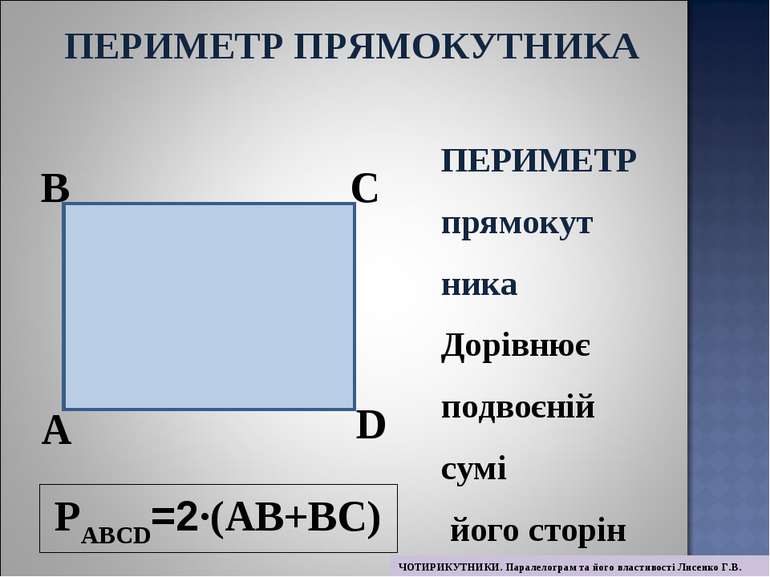
РABCD=2·(AB+BC) A B C D ПЕРИМЕТР прямокут ника Дорівнює подвоєній сумі його сторін ПЕРИМЕТР ПРЯМОКУТНИКА ЧОТИРИКУТНИКИ. Паралелограм та його властивості Лисенко Г.В.

Задача 1. Доведіть, що діагональ прямокутника ділить його на два рівні трикутники. Доведення: Розглянемо ∆АВС і ∆СDА. ∆ АВС і ∆ СDА прямокутні за умовою ( В = D = 90°), 2. ∆АВС = ∆СDА за двома катетами (АВ = СD; ВС = АD). (або за катетом і гіпотенузою). Задача 2. Доведіть, що кожна сторона прямокутника менша за його діагональ. Доведення: Провівши у прямокутнику АВСD діагональ АС утворилося два прямокутних трикутники АВС і СDА . Так як діагональ лежить проти прямого кута, а (сторони) катети проти гострих кутів, то діагональ завжди більша за катети. (проти більшого кута лежить більша сторона). А В С D ПРАЦЮЄМО РАЗОМ ЧОТИРИКУТНИКИ. Паралелограм та його властивості Лисенко Г.В.

В М С Задача 1. Дано: АВ = ВМ. Знайти 1 (мал. 1) Задача 2. Дано АВ = ВМ, 1 + D =225° А D, АD = 10 см Знайти АВ + МС. (мал. 1) Задача 3. Дано:МС = 3 см, ВМ = 7см. Знайти периметр прямокутника АВСD. (мал. 1) В Задача 4*. Дано: периметр трикутника АОD . дорівнює18 см. АС + ВD = 22 см. Знайти ВС. (мал. 2) А D Задача 5* Дано: периметр трикутника АCD дорівнює 49 см, а периметр прямокутника АВСD дорівнює 62 см. Знайти АО. (мал. 2) Задача 6*. Дано: периметр трикутника CОD дорівнює 30 см, АС + ВD = 40 см. Знайти АОD (мал. 2). 1 О С ПРАЦЮЄМО САМОСТІЙНО ЧОТИРИКУТНИКИ. Паралелограм та його властивості Лисенко Г.В.

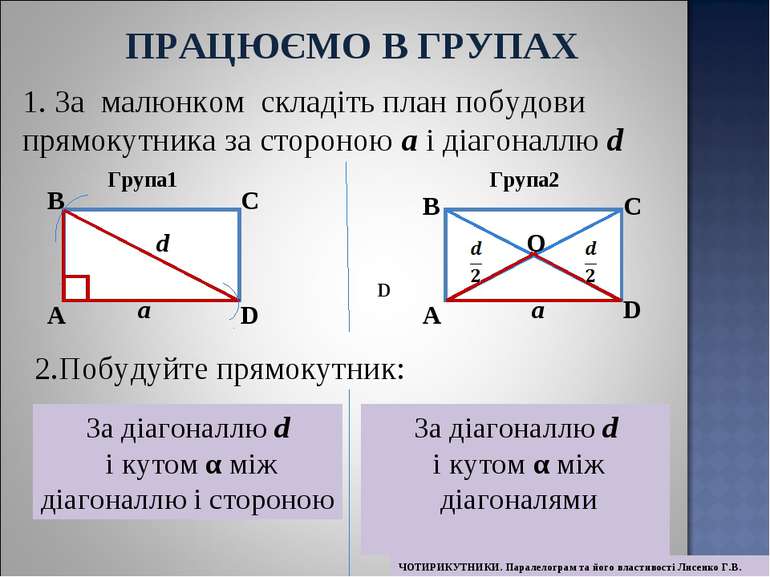
1. За малюнком складіть план побудови прямокутника за стороною a і діагоналлю d Група1 Група2 a d a A B C D A B C D O 2.Побудуйте прямокутник: D За діагоналлю d і кутом α між діагоналлю і стороною За діагоналлю d і кутом α між діагоналями ПРАЦЮЄМО В ГРУПАХ ЧОТИРИКУТНИКИ. Паралелограм та його властивості Лисенко Г.В.

Щоб чотирикутник був прямокутником , чи достатньо, щоб діагоналі в ньому були рівні? Спростувати побудовою ПІДСУМОК УРОКУ ЧОТИРИКУТНИКИ. Паралелограм та його властивості Лисенко Г.В.

1. Щоб намітити на бруску (дошці) пряму, паралельну краю бруска (дошки), теслярі використовують рейсмус. Пояснити на чому ґрунтується дія цього пристрою. 2. Якими способами можна перевірити, що даний чотирикутний предмет має форму прямокутника. Відповідь обґрунтувати. 3. Як знайти відстань між двома точками , між якими є перешкода. Домашнє завдання ЗАСТОСОВУЄМО НА ПРАКТИЦІ ЧОТИРИКУТНИКИ. Паралелограм та його властивості Лисенко Г.В.

1. М.І.Бурда, Н.А.Тарасенкова. Геометрія підручник для 8 класу загальноосвітніх навчальних закладів -К.:Зодіак-ЕКО, 2008.-240с. 2. Чекова А.М. “Геометрія 7-12 класи”: навчальний посібник, - Х.: Країна мрій,2009.-120с. 3. О.В.Темченко Геометрія. Плани- конспекти уроків Харків .:Світ дитинства, 2004.-250.с 4. О. Гайштут, Г. Литвиненко. Геометрія – це не складно Київ: “Магістр -S”, 1997. 120с. ВИКОРИСТАНА ЛІТЕРАТУРА ЧОТИРИКУТНИКИ. Паралелограм та його властивості Лисенко Г.В.