Презентація на тему:
ПРОСТІШІ МНОГОГРАННИКИ

Геометрія 10 клас § 2. ПРОСТІШІ МНОГОГРАННИКИ ТА ЇХ ПЕРЕРІЗИ За підручником М.І. Бурда, Н.А. Тарасенкова

Простіші многогранники

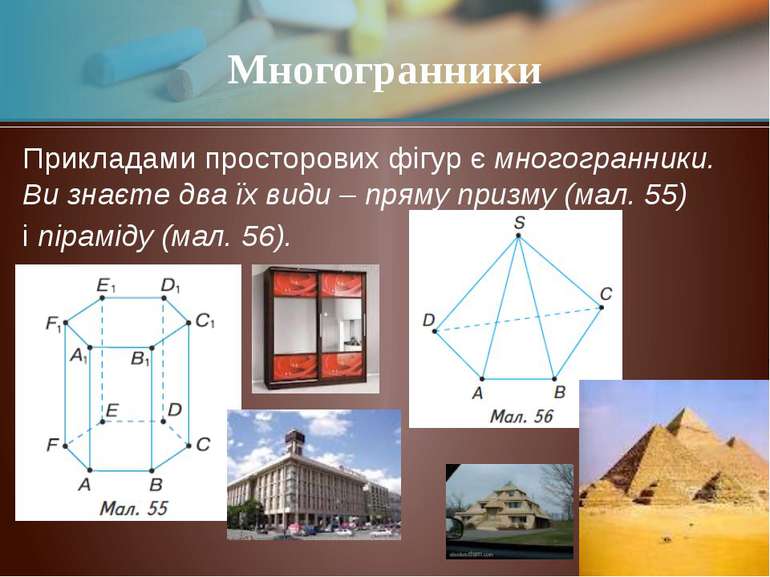
Прикладами просторових фігур є многогранники. Ви знаєте два їх види – пряму призму (мал. 55) і піраміду (мал. 56). Многогранники

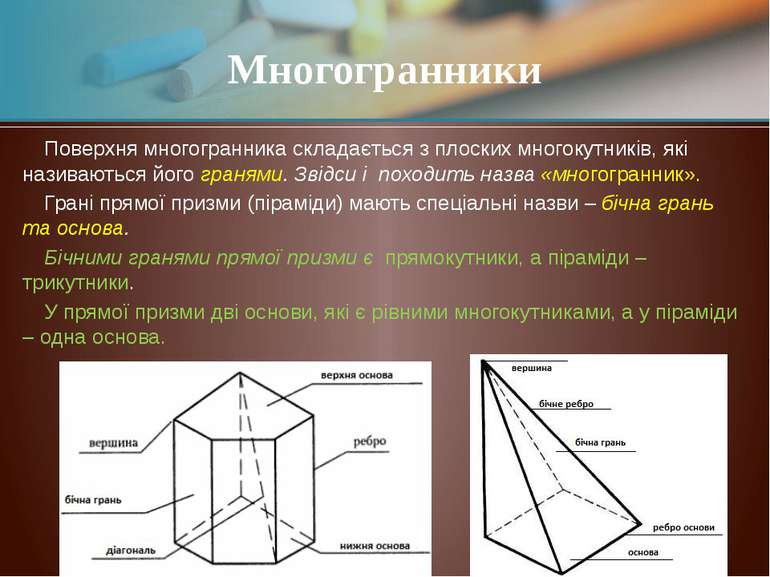
Поверхня многогранника складається з плоских многокутників, які називаються його гранями. Звідси і походить назва «многогранник». Грані прямої призми (піраміди) мають спеціальні назви – бічна грань та основа. Бічними гранями прямої призми є прямокутники, а піраміди – трикутники. У прямої призми дві основи, які є рівними многокутниками, а у піраміди – одна основа. Многогранники

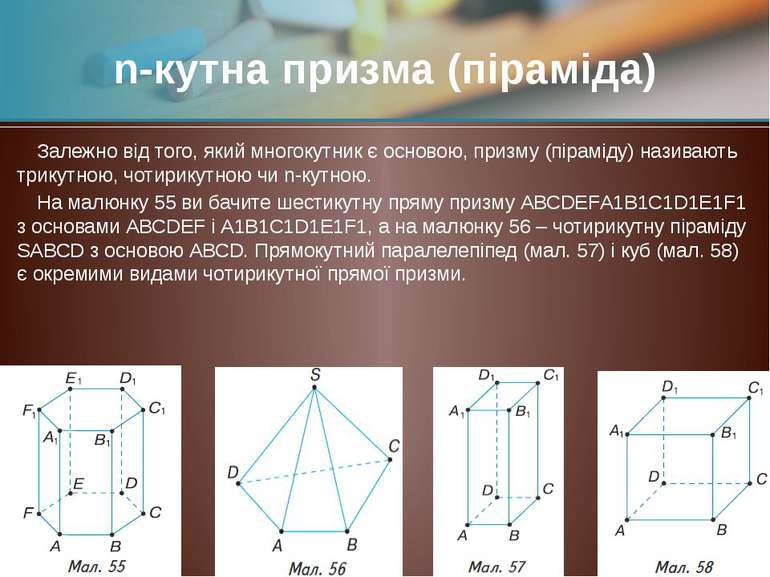
Залежно від того, який многокутник є основою, призму (піраміду) називають трикутною, чотирикутною чи n-кутною. На малюнку 55 ви бачите шестикутну пряму призму АВСDEFА1В1С1D1E1F1 з основами АВСDEF і А1В1С1D1E1F1, а на малюнку 56 – чотирикутну піраміду SАВСD з основою АВСD. Прямокутний паралелепіпед (мал. 57) і куб (мал. 58) є окремими видами чотирикутної прямої призми. n-кутна призма (піраміда)

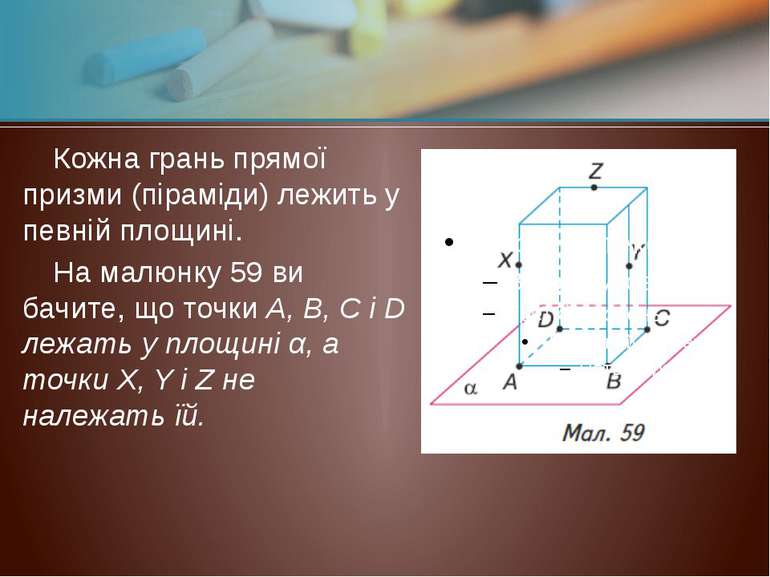
Кожна грань прямої призми (піраміди) лежить у певній площині. На малюнку 59 ви бачите, що точки А, В, С і D лежать у площині α, а точки X, Y і Z не належать їй.

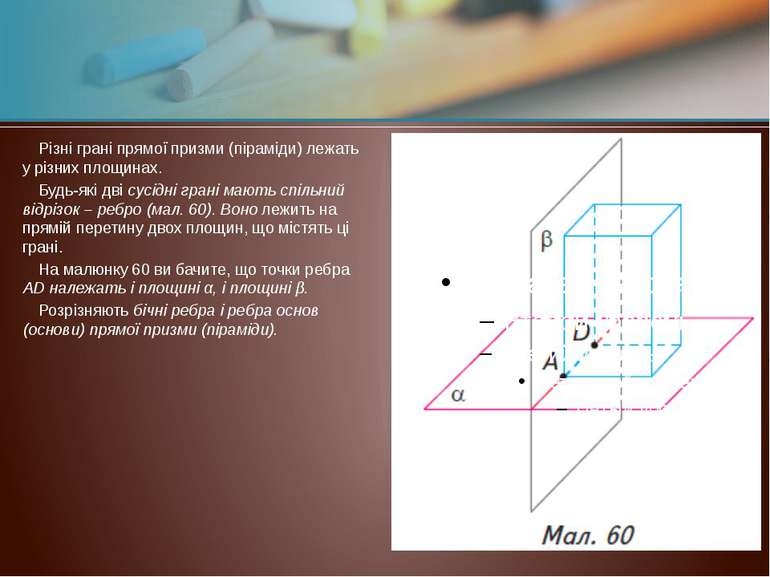
Різні грані прямої призми (піраміди) лежать у різних площинах. Будь-які дві сусідні грані мають спільний відрізок – ребро (мал. 60). Воно лежить на прямій перетину двох площин, що містять ці грані. На малюнку 60 ви бачите, що точки ребра АD належать і площині α, і площині β. Розрізняють бічні ребра і ребра основ (основи) прямої призми (піраміди).

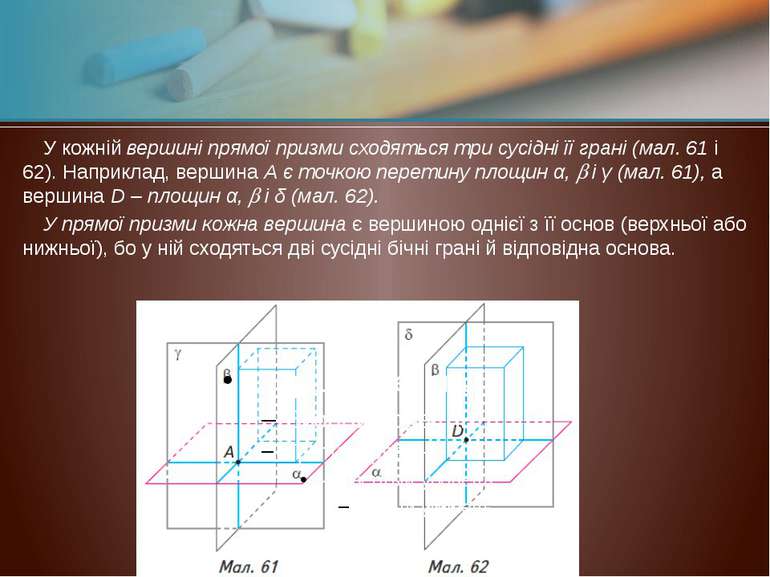
У кожній вершині прямої призми сходяться три сусідні її грані (мал. 61 і 62). Наприклад, вершина А є точкою перетину площин α, і γ (мал. 61), а вершина D – площин α, і δ (мал. 62). У прямої призми кожна вершина є вершиною однієї з її основ (верхньої або нижньої), бо у ній сходяться дві сусідні бічні грані й відповідна основа.

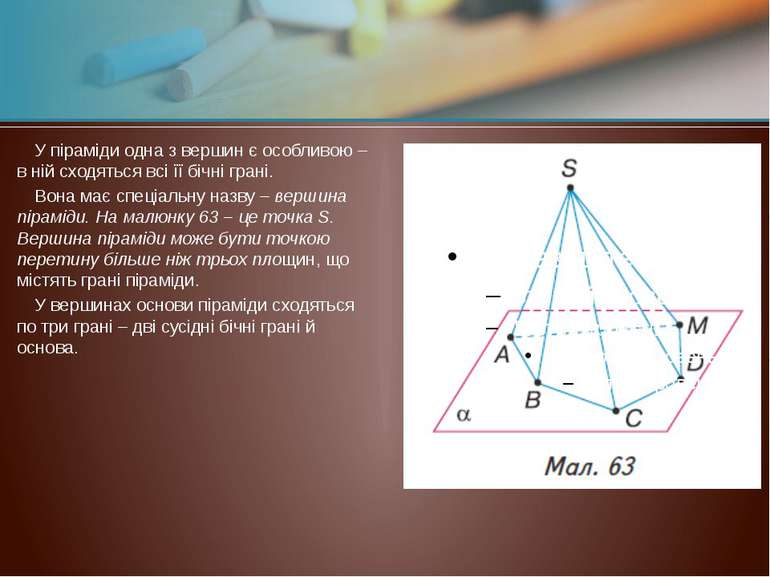
У піраміди одна з вершин є особливою – в ній сходяться всі її бічні грані. Вона має спеціальну назву – вершина піраміди. На малюнку 63 – це точка S. Вершина піраміди може бути точкою перетину більше ніж трьох площин, що містять грані піраміди. У вершинах основи піраміди сходяться по три грані – дві сусідні бічні грані й основа.

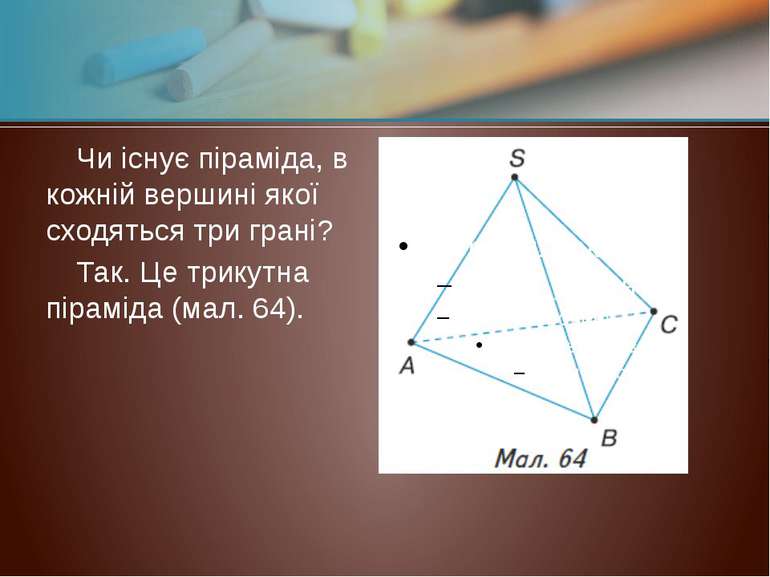
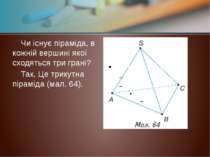
Чи існує піраміда, в кожній вершині якої сходяться три грані? Так. Це трикутна піраміда (мал. 64).

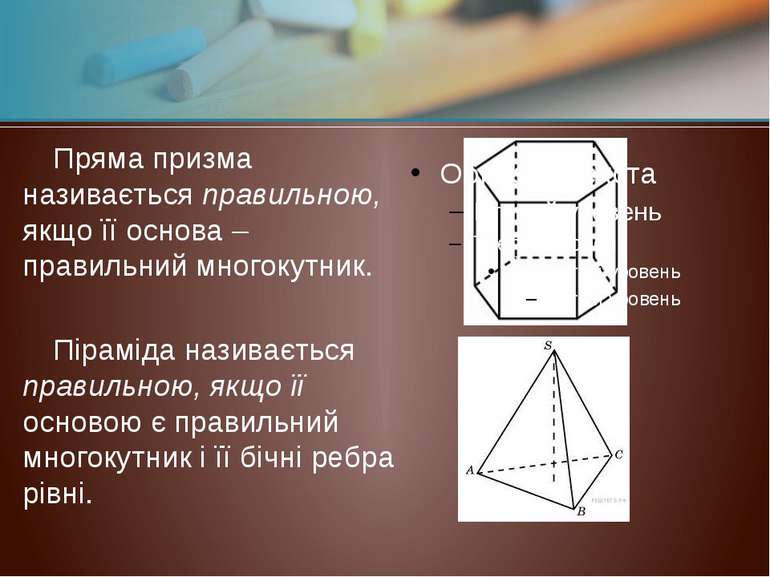
Пряма призма називається правильною, якщо її основа – правильний многокутник. Піраміда називається правильною, якщо її основою є правильний многокутник і її бічні ребра рівні.

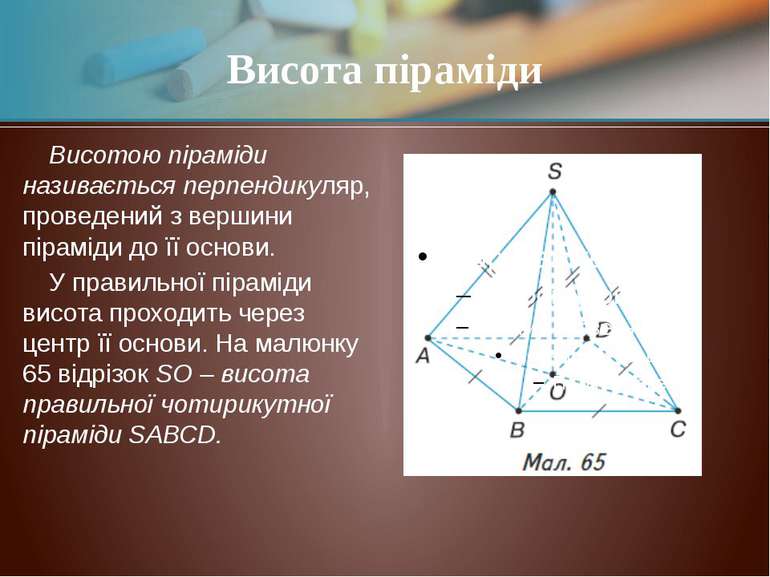
Висотою піраміди називається перпендикуляр, проведений з вершини піраміди до її основи. У правильної піраміди висота проходить через центр її основи. На малюнку 65 відрізок SО – висота правильної чотирикутної піраміди SАВСD. Висота піраміди

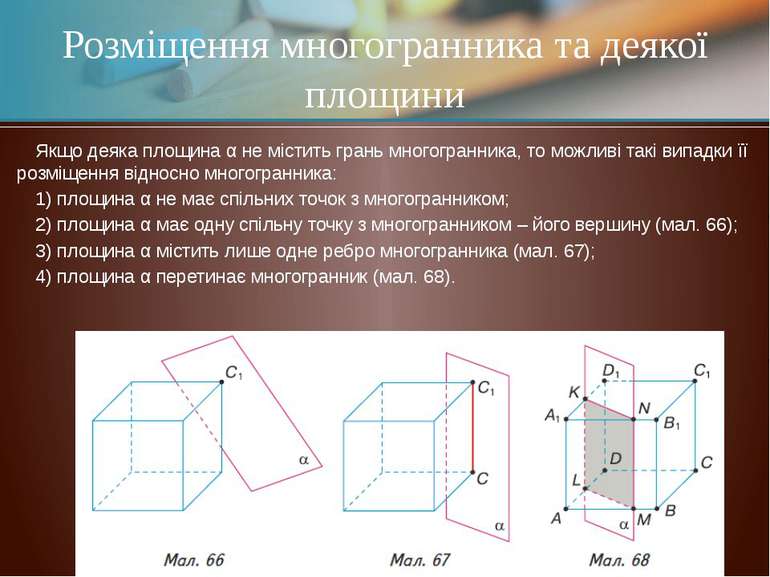
Якщо деяка площина α не містить грань многогранника, то можливі такі випадки її розміщення відносно многогранника: 1) площина α не має спільних точок з многогранником; 2) площина α має одну спільну точку з многогранником – його вершину (мал. 66); 3) площина α містить лише одне ребро многогранника (мал. 67); 4) площина α перетинає многогранник (мал. 68). Розміщення многогранника та деякої площини

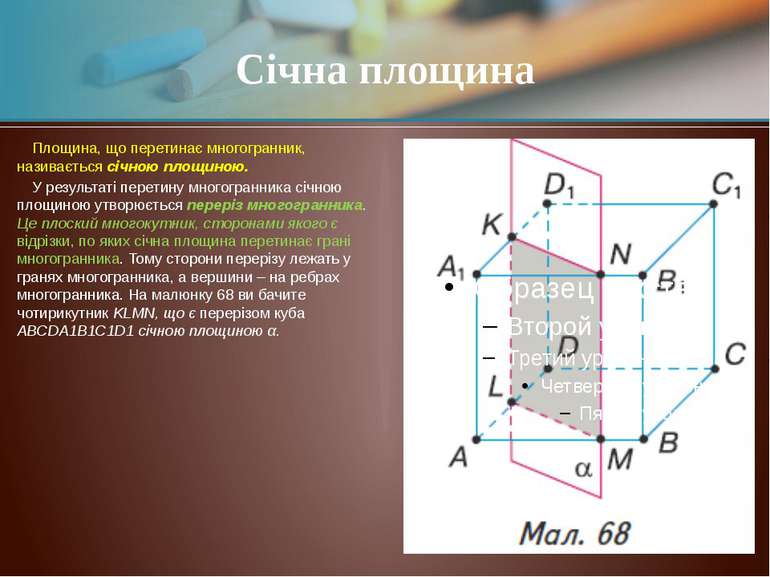
Площина, що перетинає многогранник, називається січною площиною. У результаті перетину многогранника січною площиною утворюється переріз многогранника. Це плоский многокутник, сторонами якого є відрізки, по яких січна площина перетинає грані многогранника. Тому сторони перерізу лежать у гранях многогранника, а вершини – на ребрах многогранника. На малюнку 68 ви бачите чотирикутник KLMN, що є перерізом куба АВСDА1В1С1D1 січною площиною α. Січна площина

Оскільки дві площини не можуть перетинатися більше ніж по одній прямій, то в грані многогранника не може бути більше одного відрізка перетину із січною площиною. Як і будь-яку площину, січну площину можна задати або трьома точками, що не лежать на одній прямій (мал. 69), або прямою і точкою, що не належить їй (мал. 70), або двома прямими, що перетинаються (мал. 71). Задання січної площини

Задача. на ребрах АВ, ВС і ВВ1 прямокутного паралелепіпеда АВСDА1В1С1D1 дано точки K, L і M (мал. 72). Побудуйте переріз паралелепіпеда площиною, що проходить через ці точки. Розв’язання. За умовою, точки K і M – спільні точки площини грані АВВ1А1 і січної площини. Тому ці площини перетинаються по прямій KM, а відрізок KM є відрізком перетину прямокутника АВВ1А1 із січною площиною. міркуючи аналогічно, переконуємося, що січна площина перетинає грані АВСD і ВСС1В1 паралелепіпеда по відрізках KL і ML. Проводимо відрізки KM, KL і ML. Трикутник KLM – шуканий переріз. Опорна задача

У будь-якого опуклого многогранника кількість його вершин (в), кількість граней (г) і кількість ребер (р) пов’язані такою залежністю: в + г – р = 2. Цю залежність вперше установив (1620 р.) видатний французький математик Р. Декарт (1596 – 1650), а пізніше (у 1752 р.) заново відкрив і довів німецький математик Л. Ейлер (1707 – 1783). Відповідна теорема носить ім’я Ейлера. Іноді її називають теоремою Декарта – Ейлера про многогранники. Число в + г – р називають ейлеровою характеристикою многогранника. Ейлерові характеристики широко застосовуються в теорії многогранних поверхонь. Це цікаво

Термін “призма” походить від грецького слова πrismα, що означає “розпилений”, («нечто отпиленное»). Термін “паралелепіпед” походить від грецьких слів παrαlloς – паралельний та eπiπeδon – площина. Термін “куб” (cuβox) теж античного походження. Таку назву мала гральна кістка з вирізаними на ній вічками. Її виготовляли з баранячого суглоба, який міг падати на чотири грані, але після обточування – на шість граней. Слово “піраміда” вважають чи не єдиним терміном, який дійшов до нас від стародавніх єгиптян. Воно означає “пам’ятник”, тобто обеліск, який поставлено славетній людині – фараону. Походження термінів

1. Наведіть приклади просторових фігур. 2. Поясніть, що таке пряма призма; піраміда. 3. Що є основами прямої призми? її гранями? ребрами? Вершинами? 4. Що є основою піраміди? її гранями? ребрами? Вершинами? 5. Чому призму називають трикутною, чотирикутною, n-кутною а піраміду? 6. Яка пряма призма називається правильною? а піраміда? 7. Поясніть, що таке січна площина для многогранника. Як її можна задати? 8. Що є перерізом многогранника? 9. Поясніть, що означає побудувати переріз многогранника. Первинне закріплення вивченого матеріалу

Тренувальні вправи

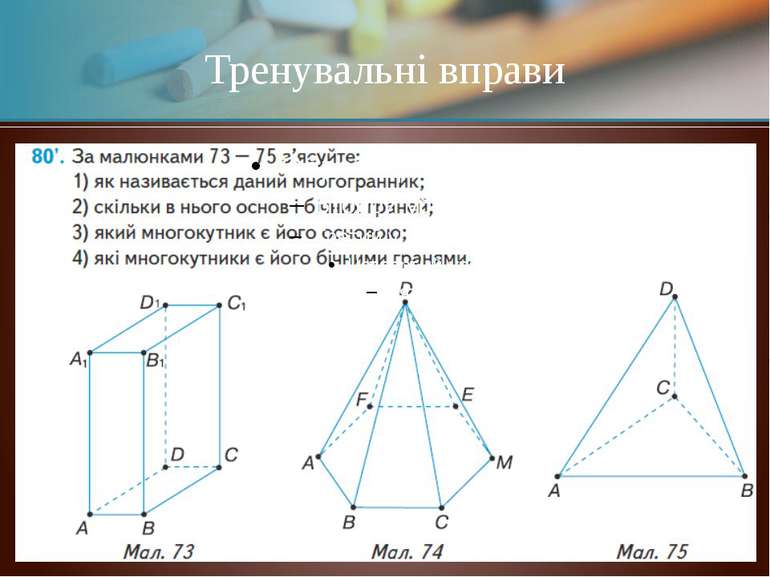
81'. Назвіть вершини і ребра многогранника (мал. 73 – 75). Які його грані: 1) сходяться у вершині: а) А; б) В ; в) С; 2) мають спільне ребро: а) AB ; б) CD ; в) AD? Вправа № 81

82'. За малюнками 76, 77 з’ясуйте: 1) яка площина перетинає даний многогранник; 2) по яких відрізках січна площина перетинає його грані; 3) який многокутник утворився в перерізі. Вправа № 82

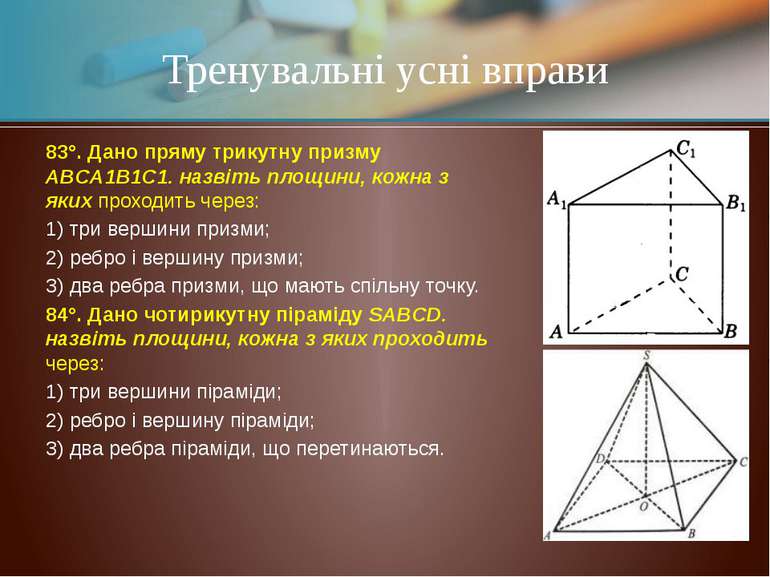
83°. Дано пряму трикутну призму ABCA1B1C1. назвіть площини, кожна з яких проходить через: 1) три вершини призми; 2) ребро і вершину призми; 3) два ребра призми, що мають спільну точку. 84°. Дано чотирикутну піраміду SABCD. назвіть площини, кожна з яких проходить через: 1) три вершини піраміди; 2) ребро і вершину піраміди; 3) два ребра піраміди, що перетинаються. Тренувальні усні вправи

85°. Чи є правильною пряма призма, якщо її основа: 1) квадрат; 2) ромб; 3) трапеція? Відповідь поясніть. 86°. Чи можна вважати правильною піраміду, в якої: 1) основа – рівнобедрений трикутник, а бічні ребра однакової довжини; 2) основа – правильний трикутник; 3) основа – правильний трикутник, а бічні ребра не однакової довжини; 4) основа – рівносторонній трикутник, а бічні ребра дорівнюють стороні основи? Відповідь поясніть. Тренувальні усні вправи

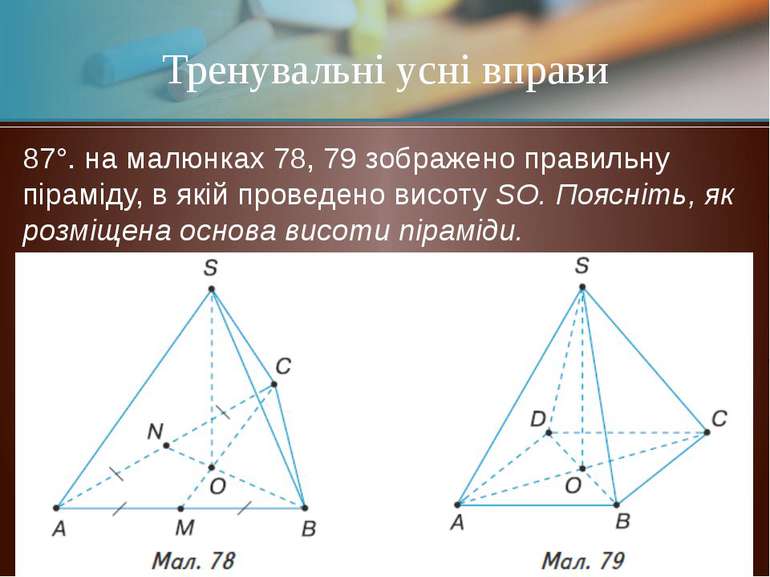
87°. на малюнках 78, 79 зображено правильну піраміду, в якій проведено висоту SО. Поясніть, як розміщена основа висоти піраміди. Тренувальні усні вправи

Вправа № 88 Дано: 1) прямокутний паралелепіпед АВСDА1В1С1D1; 2) куб АВСDА1В1С1D1. Проведіть січну площину через: 1) вершини А, С, D1; 2) вершини В1, D1, С; 3) ребра ВС і А1D1; 4) ребра АА1 і СС1. Який многокутник дістали в перерізі? Задачі на побудову перерізу

89°. Накресліть піраміду: 1) трикутну; 2) чотирикутну; 3) шестикутну. Позначте середини її бічних ребер і через них проведіть січну площину. Який многокутник дістали в перерізі? Робота в парах

91. Виведіть формулу для обчислення кількості вершин n-кутної: 1) призми; 2) піраміди. 92. Виведіть формулу для обчислення кількості ребер n-кутної: 1) призми; 2) піраміди. 93. Виведіть формулу для обчислення кількості граней n-кутної: 1) призми; 2) піраміди. Робота в парах

94. Скільки вершин п’ятикутної призми АВСDEА1В1С1D1E1 не лежить: 1) на ребрі DE; 2) на ребрі СС1; 3) у площині грані ВСD; 4) у площині грані DED1? 95. Чи залежить кількість вершин (ребер, граней) у призми від того, що її основою є правильний многокутник? а у піраміди? 96. У кубі АВСDА1В1С1D1 задано точку: 1) P на ребрі АА1; 2) Q на ребрі АD. Площини яких граней куба перетинає пряма, що лежить у площині грані куба і проходить через дану точку та одну з вершин куба? Скільки таких прямих можна провести? Самостійне виконання вправ з обґрунтуванням відповіді

99. Побудуйте переріз чотирикутної піраміди SАВСD площиною, яка проходить через: 1) середини ребер SА, АВ, АD ; 2) середину ребра АВ і медіану грані SВС ; 3) медіани граней SАВ і SВС. Чи завжди задача має розв’язок? Самостійна робота. Взаємоперевірка

106. З дерев’яного кубика треба виточити правильну піраміду: чотирикутну; 2) трикутну. Поясніть, як це можна зробити. Застосування на практиці вивченого матеріалу