Презентація на тему:
Поняття про теорему Піфагора та способи її доведення

Розглянути теорему Піфагора як джерело надзвичайних математичних відкриттів

Дослідити сутність виникнення теореми Піфагора. Ознайомитися з біографією Піфагора. З’ясувати історичну сутність теореми. Вивчити перші способи формулювання теореми. Пояснити, як доводили цю теорему в різні часи різні народи: доведення методом розкладання; доведення методом доповнення; інші доведення. Визначити, де і як застосовується теорема Піфагора в даний час.

Великий учений Піфагор народився близько 570 р. до н.е. на острові Самосе. Серед учителів юного Піфагора традиція називає імена старця Гермодаманта і Ферекида Сиросського. В Кротоні Піфагор заснував щось на зразок релігійно-етичного братства або таємного чернечого ордена («піфагорійці»), члени якого зобов'язали вести так званий піфагорійський спосіб життя. Це був одночасно і релігійний союз, і політичний клуб, і наукове суспільство. Потрібно сказати, що деякі з проповідуючих Піфагором принципів гідні наслідування і зараз. ... Пройшло 20 років. Слава про братство рознеслася по всьому світу. Одного разу до Піфагора приходить Килон, людина багата, але зла, бажаючи сп'яну вступити в братство. Діставши відмову, Килон розпочинає боротьбу з Піфагором, скориставшись підпалом його будинку. При пожежі піфагорійці врятували життя своєму вчителю ціною своєю, після чого Піфагор затужив і незабаром покінчив життя самогубством.

У "Переліку математиків", приписуваному Евдему, про Піфагора сказано так: "Як передають, Піфагор перетворив заняття цієї галузі (геометрії) на справжню науку, розглядаючи її основи з вищої точки зору і досліджуючи її теорії менш матеріальним і більш розумовим способом". Піфагору приписуються створення основ планіметрії, правил побудови деяких правильних многокутників і багатогранників, введення і обов'язково широкого використання доведення в геометрію, створення вчення про подібність, доведення теореми про сторони прямокутного трикутника. Піфагор – математик був і одним з найбільших філософів, учення якого, на жаль, не збереглося до наших днів. Піфагор заснував філософську школу – піфагореїзм, в якій велике значення надається музиці і числам. Числа у піфагорійців виступають універсальними об'єктами, до яких передбачалося звести не лише математичні побудови, але і все різноманіття дійсності. Фізичні, етичні, соціальні і релігійні поняття отримали математичну окраску. Науці про числа та інші математичні об'єкти відводиться основне місце в системі світогляду, тобто фактично математика оголошується філософією.

Наведемо різні формулювання теореми Піфагора в перекладі з грецької, латинської і німецької мов. У Евкліда ця теорема носить (дослівний переклад): "У прямокутному трикутнику квадрат сторони, натягнутої над прямим кутом, дорівнює квадратам на сторонах, що утворюють прямий кут". Латинський переклад арабського тексту в перекладі на російський свідчить: "У всякому прямокутному трикутнику квадрат, утворений на стороні, натягнутій над прямим кутом, дорівнює сумі двох квадратів, утворених на двох сторонах, що утворюють прямий кут". У даний час відомо, що ця теорема не була відкрита Піфагором. Проте одні вважають, що Піфагор першим дав її повноцінне доведення, а інші заперечують це. Деякі приписують Піфагору доведення, яке Евклід розкриває в першій книзі своїх “Начал”. З іншого боку, Прокл стверджує, що доведення в "Началах" належить самому Евкліду. Як ми бачимо, історія математики майже не зберегла достовірних даних про життя Піфагора і його математичну діяльність. Проте легенда повідомляє навіть найближчі обставини, що супроводжували відкриття теореми.

Найпростіший спосіб доведення теореми виходить в найпростішому випадку рівнобедреного прямокутного трикутника. Насправді, досить просто подивитися на мозаїку рівнобедрених прямокутних трикутників, щоб переконатися в справедливості теореми. Наприклад, для трикутника ABC : квадрат, побудований на гіпотенузі АС, містить 4 початкові трикутники, а квадрати, побудовані на катетах, - по два. Теорема доведена.

Разом з доведеннями методом розкладання можна навести приклади доведення за допомогою віднімання, названих також доведеннями методом доповнення. Загальна ідея таких доведень полягає в наступному. Від двох рівних площ потрібно відняти рівновеликі частини так, щоб в одному випадку залишилися два квадрати, побудовані на катетах, а в іншому - квадрат, побудований на гіпотенузі. Адже якщо в рівності В-А=С і В1-А1=С1частина А рівновелика частині А1, а частина В рівновелика В1, то частини 3 і С1 також рівновеликі. Пояснимо цей метод на прикладі. На малюнку до звичайної піфагорової фігури приставлені зверху і знизу трикутники 2 і 3, рівні вихідному трикутнику 1. Пряма DG обов'язково пройде через C. Відмітимо тепер (далі ми це доведемо), що шестикутники DABGFE і CAJKHB рівновеликі. Якщо ми від першого з них віднімемо трикутники 1 і 2, то залишаться квадрати, побудовані на катетах, а якщо від другого шестикутника віднімемо рівні трикутники 1 і 3, то залишиться квадрат, побудований на гіпотенузі. Звідси випливає, що квадрат, побудований на гіпотенузі, рівновеликий сумі квадратів, побудованих на катетах. Залишається довести, що наші шестикутники рівновеликі. Відмітимо, що пряма DG ділить верхній шестикутник на рівновеликі частини; те ж саме можна сказати про пряму CK і нижній шестикутник. Обернемо чотирикутник DABG, що становить половину шестикутника DABGFE, навколо точки А за годинниковою стрілкою на кут 900; тоді він з’єднається з чотирикутником CAJK і складатиме половину шестикутника CAJKHB. Тому шестикутники DABGFE і CAJKHB рівновеликі.

Познайомимося з іншим доведенням - методом віднімання. Знайоме нам креслення теореми Піфагора укладемо в прямокутну рамку, напрями сторін якої збігаються з напрямами катетів трикутника. Продовжимо деякі з відрізків фігури так, як вказано на малюнку, при цьому прямокутник розпадається на декілька трикутників, прямокутників і квадратів. Викинемо з прямокутника спочатку декілька частин так, аби залишився лише квадрат, побудований на гіпотенузі. Ці частини наступні: трикутники 1, 2, 3, 4; прямокутник 5; прямокутник 6 і квадрат 8; прямокутник 7 і квадрат 9; Потім викинемо з прямокутника частини так, щоб залишилися лише квадрати, побудовані на катетах. Цими частинами будуть: прямокутники 6 і 7; прямокутник 5; прямокутник 1 (заштрихований); прямокутник 2 (заштрихований); Нам залишилося лише показати, що частини, які ми відняли, рівновеликі. Це легко побачити через розташування фігур. З малюнка ясно, що: прямокутник 5 рівновеликий самому собі; чотири трикутники 1, 2, 3, 4 рівновеликі двом прямокутникам 6 і 7; прямокутник 6 і квадрат 8, узяті разом, рівновеликі прямокутнику 1 (заштрихований); прямокутник 7 разом з квадратом 9 рівновеликі прямокутнику 2 (заштрихований). Доведення закінчено.

Цей спосіб доведення був наведений Евклідом в його "Началах". За свідченням Прокла (Візантія), воно винайдене самим Евклідом. Доведення Евкліда наведене в пропозиції 47 першої книги "Начал". На гіпотенузі і катетах прямокутного трикутника АВС будуються відповідні квадрати і доводиться, що прямокутник BJLD рівновеликий квадрату ABFH, а прямокутник JCEL - квадрату АСКG. Тоді сума квадратів на катетах дорівнюватиме квадрату на гіпотенузі. Насправді, трикутники ABD і BFC рівні за двома сторонами і кутом між ними: FB = AB, BC = BD; РFBC = d + РABC = РABD Але SABD =  S BJLD, оскільки в трикутника ABD і прямокутника BJLD основа BD, а висота LD. Аналогічно: SFBC=S ABFH (BF-спільна основа, АВ - спільна висота). Звідси, враховуючи, що SABD=SFBC маємо SBJLD=SABFH. Аналогічно, використовуючи рівність трикутників ВСК і АСЕ, доводиться, що SJCEL=SACKG. Отже SABFH+SACKG= SBJLD+SJCEL= SBCED що і потрібно було довести.

Наведемо ще одне доведення, яке має обчислювальний характер, проте дуже відрізняється від всіх попередніх. Воно опубліковане англійцем Хоукинсом в 1909 році; чи було воно відомо до цього важко сказати. Прямокутний трикутник ABC з прямим кутом C обернемо на 90° так, щоб він зайняв положення A'CB'. Продовжимо гіпотенузу A'В' за точку A' до перетину з лінією АВ в точці D. Відрізок В'D буде висотою трикутника В'АВ. Розглянемо тепер заштрихований чотирикутник A'АВ'В . Його можна розкласти на два рівнобедрені трикутники САА' і СВВ' (або на два трикутники A'В'А і A'В'В). SCAA'= SCBB‘= SA'AB'B= Трикутники A'В'А і A'В'В мають загальну основу і висоту DA і DB, тому : SA'AB'B= с Порівнюючи два отримані вирази для обчислення площі, отримаємо: Теорема доведена.

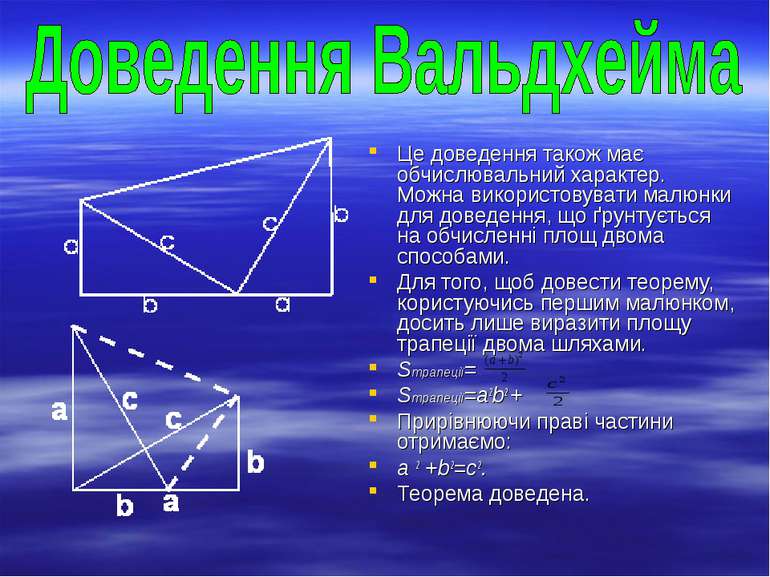
Це доведення також має обчислювальний характер. Можна використовувати малюнки для доведення, що ґрунтується на обчисленні площ двома способами. Для того, щоб довести теорему, користуючись першим малюнком, досить лише виразити площу трапеції двома шляхами. Sтрапеції= Sтрапеції=a2b2 + Прирівнюючи праві частини отримаємо: а 2 +b2=c2. Теорема доведена.

Доведення індійського математика Басхари показано на малюнку. У пояснення до нього він написав лише одне слово: "Дивися!“ Учені вважають, що він виражав площу квадрата, побудованого на гіпотенузі, як суму площ трикутників і площу квадрата (а-b)2. Отже: с2= +(а-b)2 c=2ab+a2-2ab+b2 с2=a2+b2. Теорема доведена.

Для того, щоб довести теорему, доведемо наступне: якщо на катетах і на гіпотенузі прямокутного трикутника побудовані які завгодно подібні між собою фігури Fa, Fb, Fc, так, що катети і гіпотенуза є подібними відрізками цих фігур, то маємо рівність: Fa+Fb=Fc. Для доведення скористаємося наступною теоремою з теорії подібності: площі подібних многокутників відносяться як квадрати подібних сторін. Якщо через Fa, Fb, Fc позначити площі подібних многокутників, побудованих на катетах а, b і гіпотенузі с прямокутного трикутника, то згідно з допоміжною теоремою можна написати: Fa:Fb:Fc=a2:b2:c2. Ця пропорція означає, що можна знайти число ( коефіцієнт пропорційності) таке, що Fa=ka2, Fb=kb2, Fc=kc2. Помноживши обидві частини рівності на k і зважаючи на попередню рівність, отримаємо: Fa+Fb=Fc. Якщо рівність Fa+Fb=Fc має місце хоч би для однієї трійки подібних між собою многокутників, побудованих на катетах і на гіпотенузі прямокутного трикутника АВС так, що АС, ВС і АВ є подібні відрізки цих многокутників, то ka²+kb²=kc² (де k має якесь певне значення, залежне від вибору многокутників, - не має різниці, яке саме). Але звідси випливає, що а2+b2=с2, а звідси випливає той факт, що рівність Fa+Fb=Fc виконується для будь-яких побудованих на сторонах прямокутного трикутника подібних многокутників, зокрема, і для квадратів.

Нехай АВС - прямокутний трикутник з прямим кутом при вершині С, побудований на векторах. Тоді справедлива векторна рівність: звідки маємо: Підносячи обидві частини до квадрату, отримаємо Оскільки, , то , звідки або с2=a2+b2. Нами знову доведена теорема Піфагора. Якщо трикутник АВС - довільний, то ця формула дає теорему косинусів, яка узагальнює теорему Піфагора.

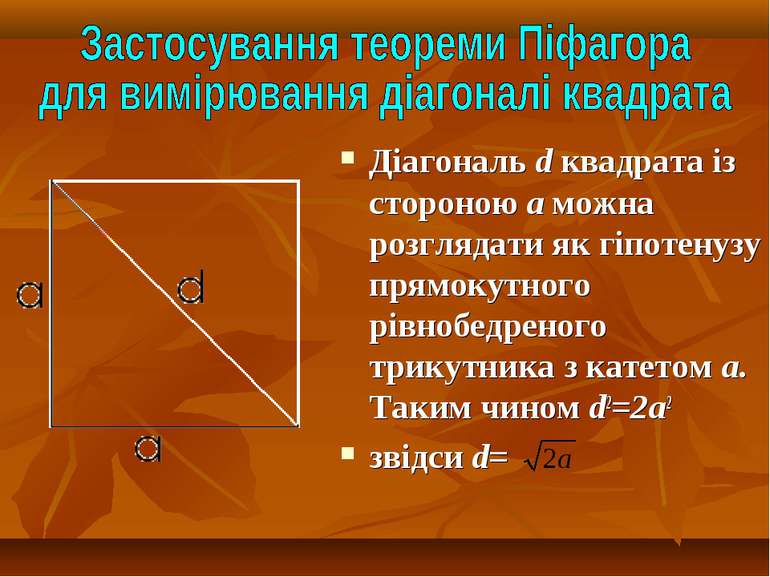
Діагональ d квадрата із стороною а можна розглядати як гіпотенузу прямокутного рівнобедреного трикутника з катетом а. Таким чином d2=2a2 звідси d=

Діагональ d прямокутника із сторонами а і b обчислюється подібно до того, як обчислюється гіпотенуза прямокутного трикутника з катетами а і b. Ми маємо d2=a2+b2.

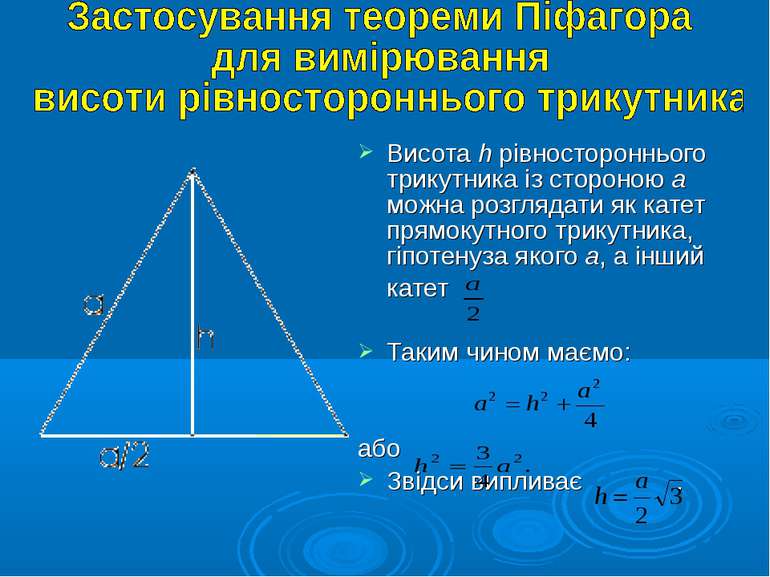
Висота h рівностороннього трикутника із стороною а можна розглядати як катет прямокутного трикутника, гіпотенуза якого а, а інший катет Таким чином маємо: або Звідси випливає .

Висновки Дякуючи тому, що теорема Піфагора дозволяє знаходити довжину відрізка (гіпотенузи), не вимірюючи його, вона ніби відкриває шлях з прямої на площину, з площини в трьохвимірний простір і далі – багатовимірний простір. Цим визначається її особлива значущість для геометрії і математики в цілому. У деякій мірі в теоремі Піфагора, як у зерні, знаходиться вся евклідова планіметрія. Теорема Піфагора лежит в основі багатьох загальних метричних співвідношень на площині і в просторі. Загалом на неї спирається і тригонометрія. Праці Піфагора можна вважати відправним пунктом дослідження невизначених алгебраїчних нерівностей.