Презентація на тему:
ПОНЯТТЯ ПРО МНОГОГРАННИКИ

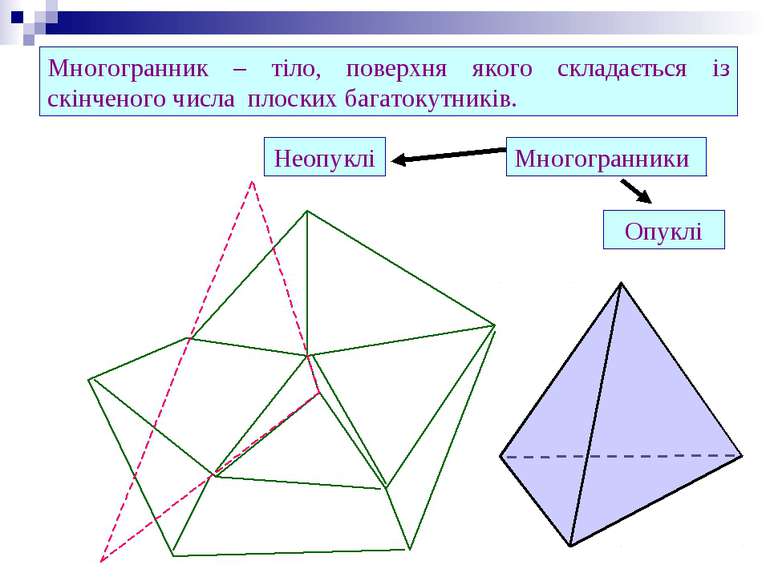
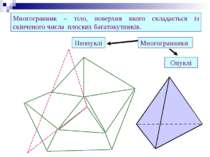
Многогранник – тіло, поверхня якого складається із скінченого числа плоских багатокутників. Многогранники Опуклі Неопуклі

Многогранники Призми Піраміди Інші многогранники

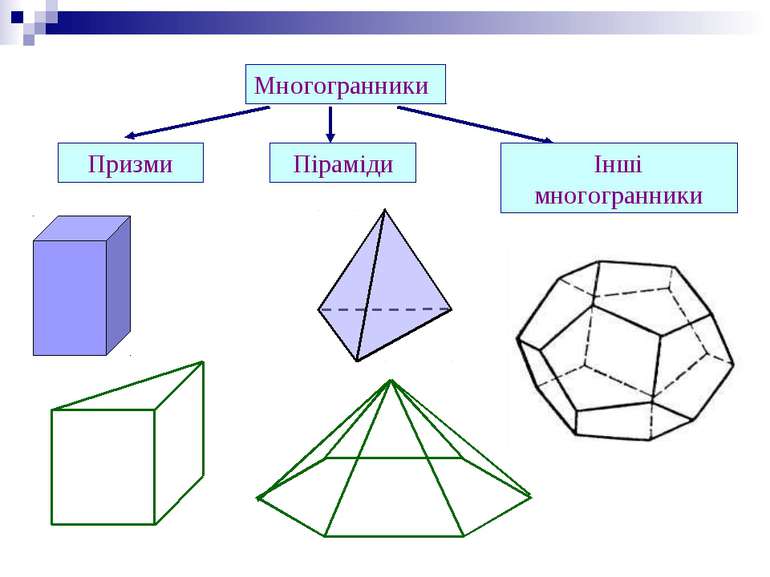
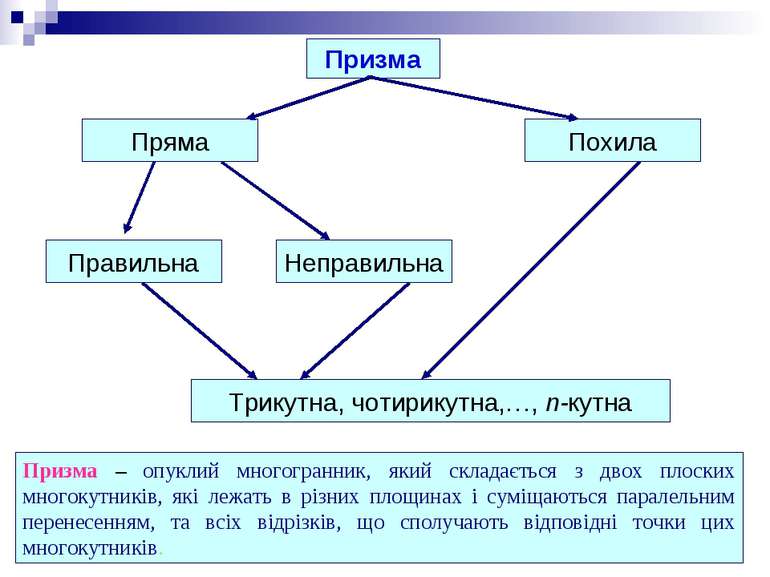
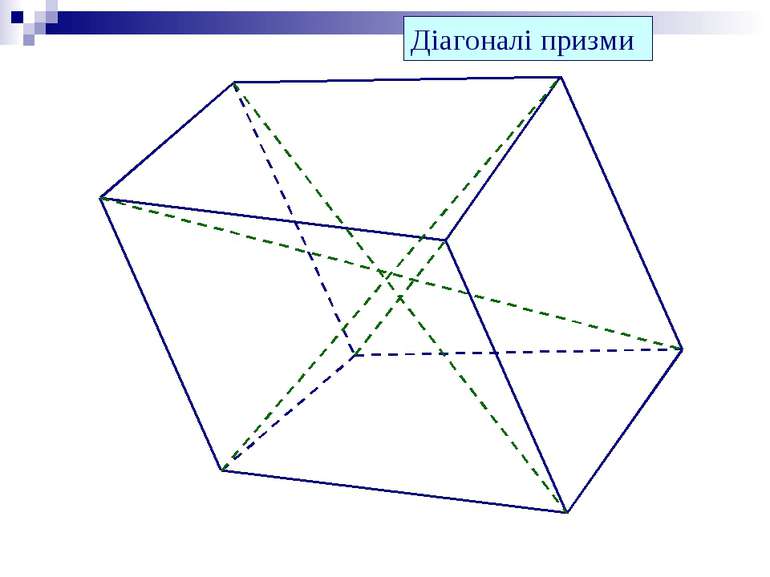
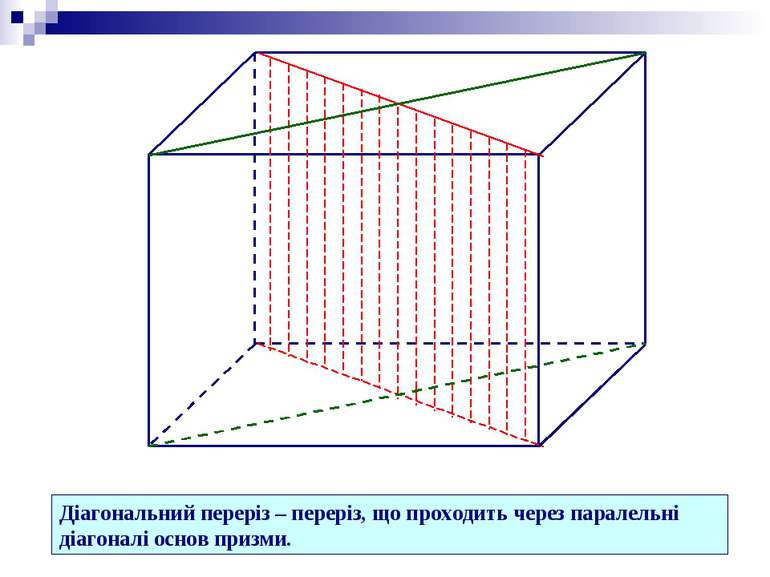
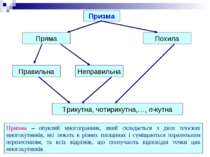
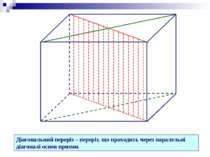
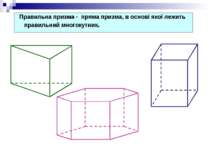
Призма Пряма Похила Правильна Неправильна Трикутна, чотирикутна,…, n-кутна Призма – опуклий многогранник, який складається з двох плоских многокутників, які лежать в різних площинах і суміщаються паралельним перенесенням, та всіх відрізків, що сполучають відповідні точки цих многокутників.

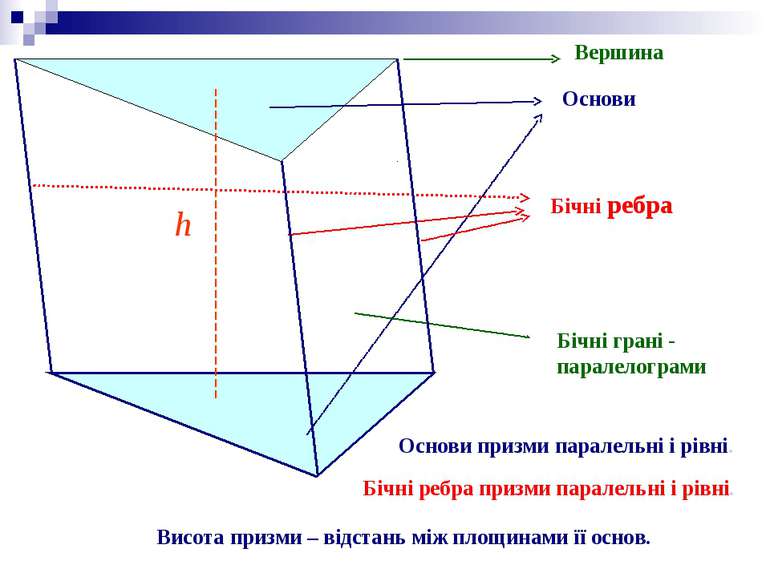
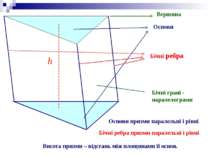
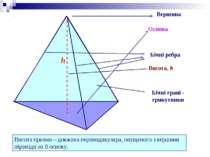
Вершина Основи Бічні ребра Бічні грані - паралелограми Основи призми паралельні і рівні. Бічні ребра призми паралельні і рівні. Висота призми – відстань між площинами її основ. h

Діагоналі призми

Діагональний переріз – переріз, що проходить через паралельні діагоналі основ призми.

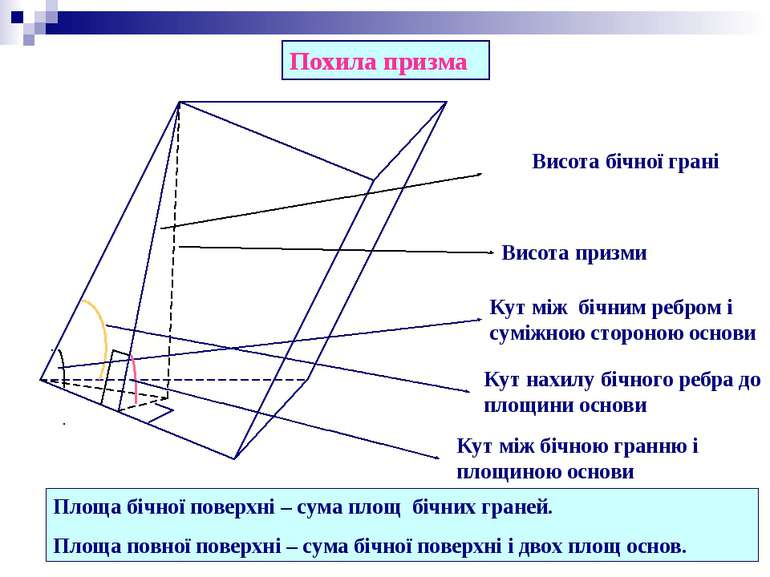
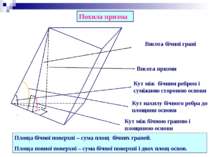
Похила призма Висота бічної грані Висота призми Кут між бічним ребром і суміжною стороною основи Кут нахилу бічного ребра до площини основи Кут між бічною гранню і площиною основи Площа бічної поверхні – сума площ бічних граней. Площа повної поверхні – сума бічної поверхні і двох площ основ.

Похилі призми

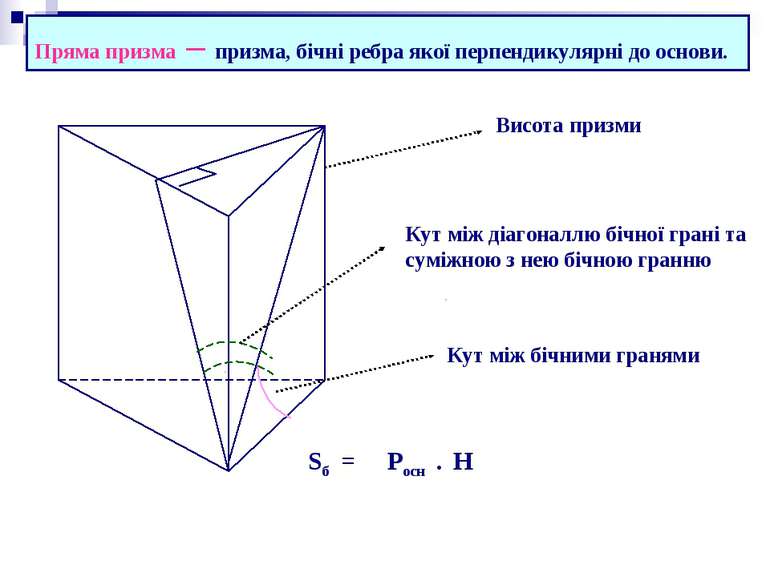
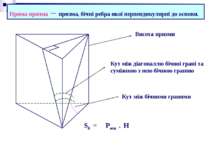
Пряма призма – призма, бічні ребра якої перпендикулярні до основи. Висота призми Кут між бічними гранями Кут між діагоналлю бічної грані та суміжною з нею бічною гранню Sб = Росн . H

Правильна призма - пряма призма, в основі якої лежить правильний многокутник.

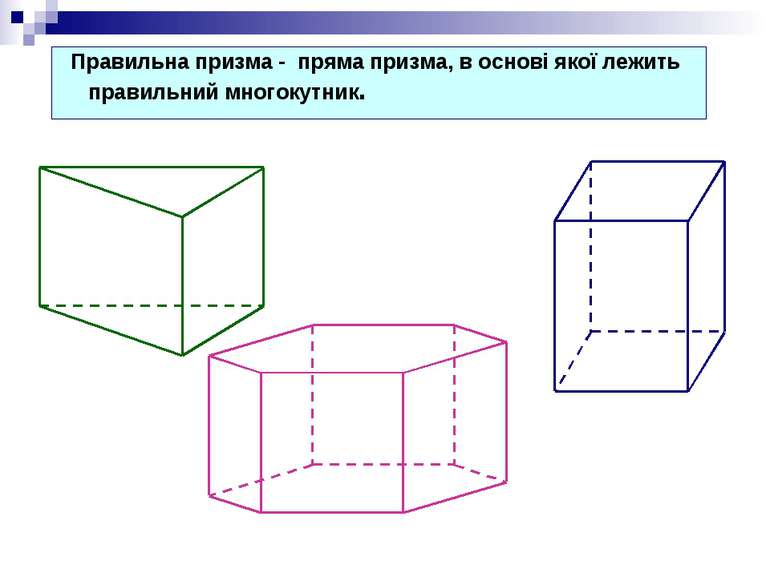
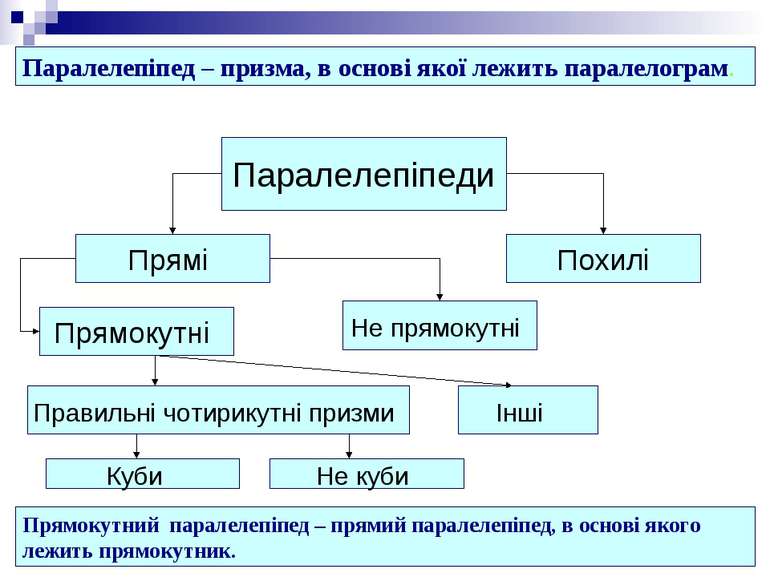
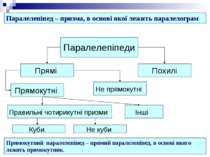
Паралелепіпеди Прямі Похилі Прямокутні Не прямокутні Правильні чотирикутні призми Інші Куби Не куби Паралелепіпед – призма, в основі якої лежить паралелограм. Прямокутний паралелепіпед – прямий паралелепіпед, в основі якого лежить прямокутник.

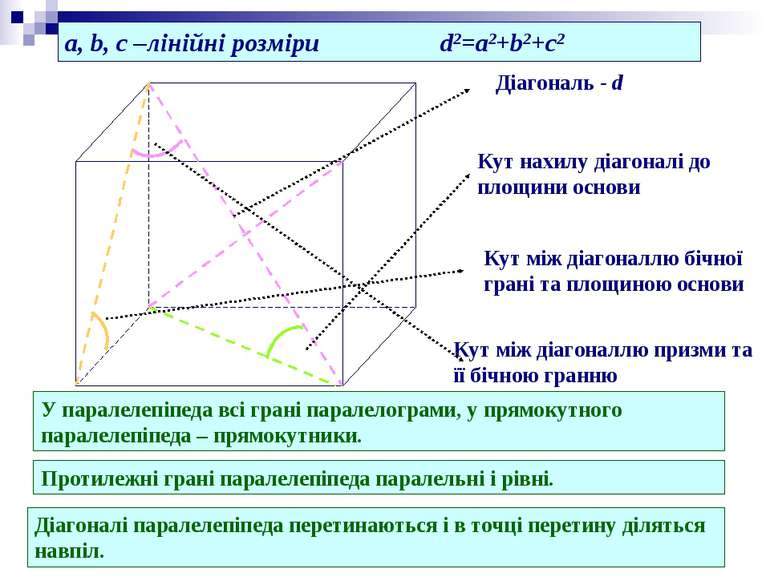
Діагональ - d Кут нахилу діагоналі до площини основи Кут між діагоналлю бічної грані та площиною основи Кут між діагоналлю призми та її бічною гранню Протилежні грані паралелепіпеда паралельні і рівні. Діагоналі паралелепіпеда перетинаються і в точці перетину діляться навпіл. a, b, c –лінійні розміри d2=a2+b2+c2 У паралелепіпеда всі грані паралелограми, у прямокутного паралелепіпеда – прямокутники.

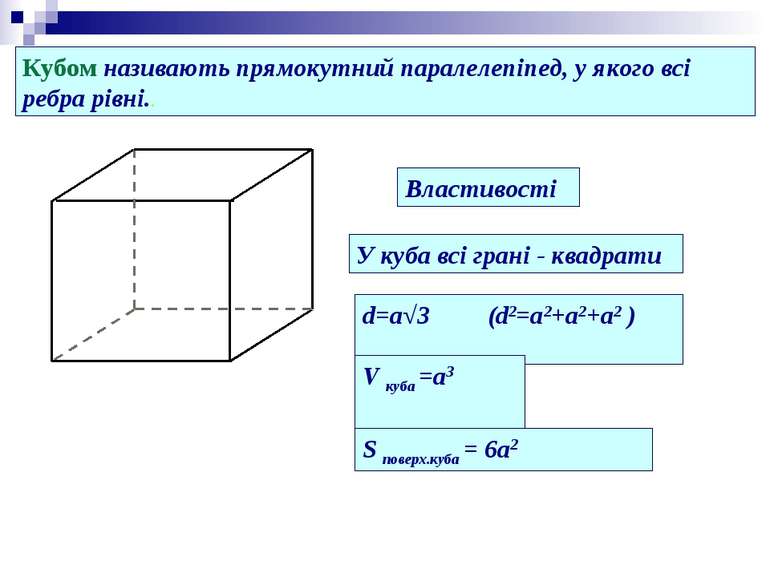
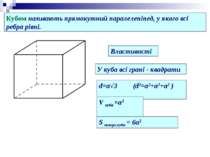
Кубом називають прямокутний паралелепіпед, у якого всі ребра рівні.. Властивості У куба всі грані - квадрати d=a√3 (d2=a2+a2+a2 ) V куба =a3 S поверх.куба = 6a2

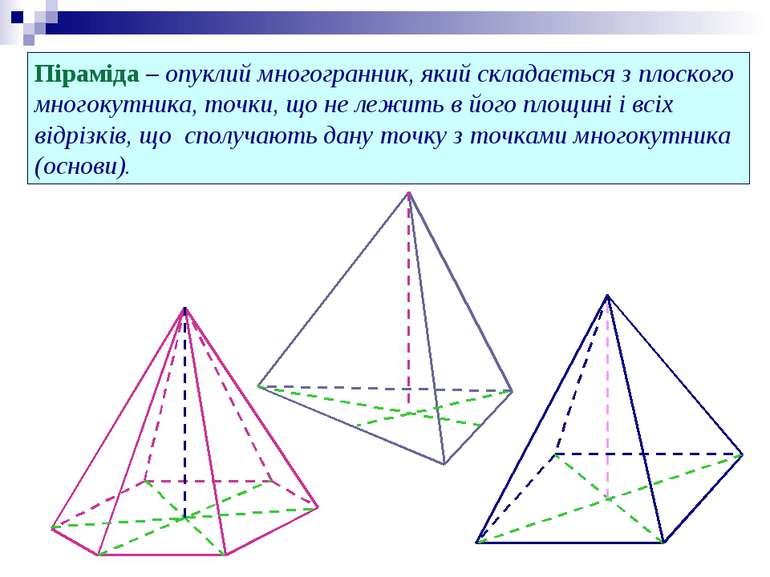
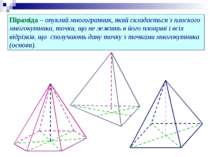
Піраміда – опуклий многогранник, який складається з плоского многокутника, точки, що не лежить в його площині і всіх відрізків, що сполучають дану точку з точками многокутника (основи).

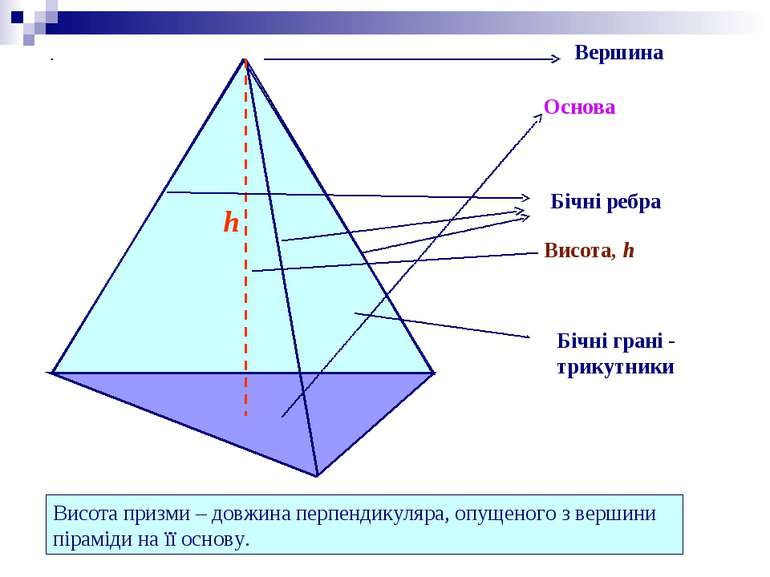
Вершина Основа Бічні ребра Бічні грані - трикутники Висота призми – довжина перпендикуляра, опущеного з вершини піраміди на її основу. h Висота, h

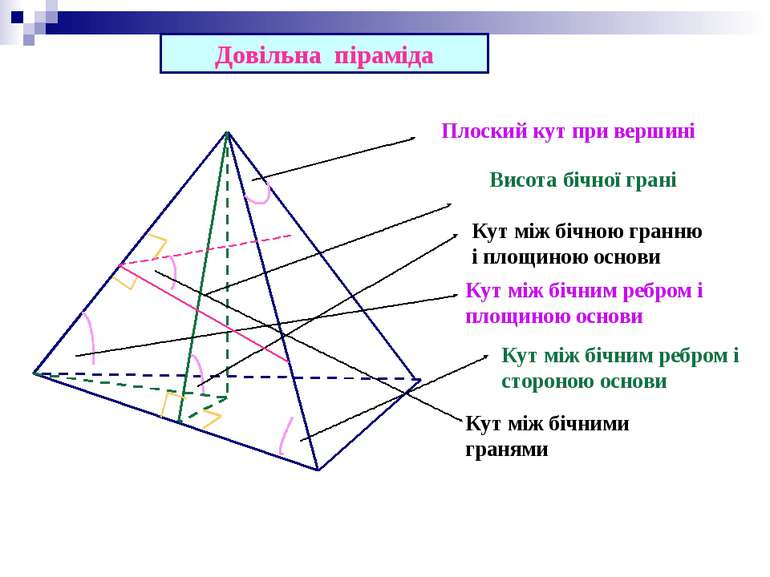
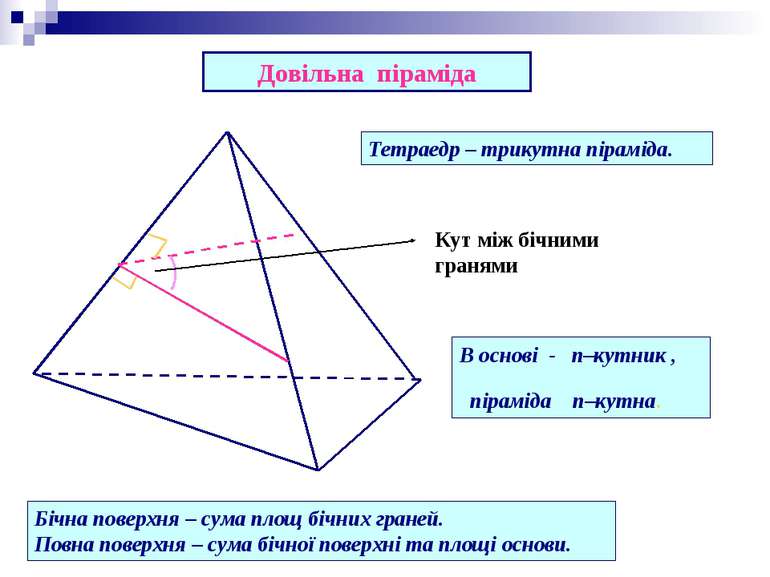
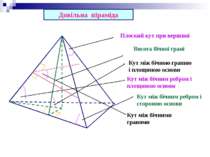
Довільна піраміда Висота бічної грані Кут між бічною гранню і площиною основи Кут між бічним ребром і площиною основи Кут між бічним ребром і стороною основи Плоский кут при вершині Кут між бічними гранями

Кут між бічними гранями Довільна піраміда Бічна поверхня – сума площ бічних граней. Повна поверхня – сума бічної поверхні та площі основи. Тетраедр – трикутна піраміда. В основі - n–кутник , піраміда n–кутна.

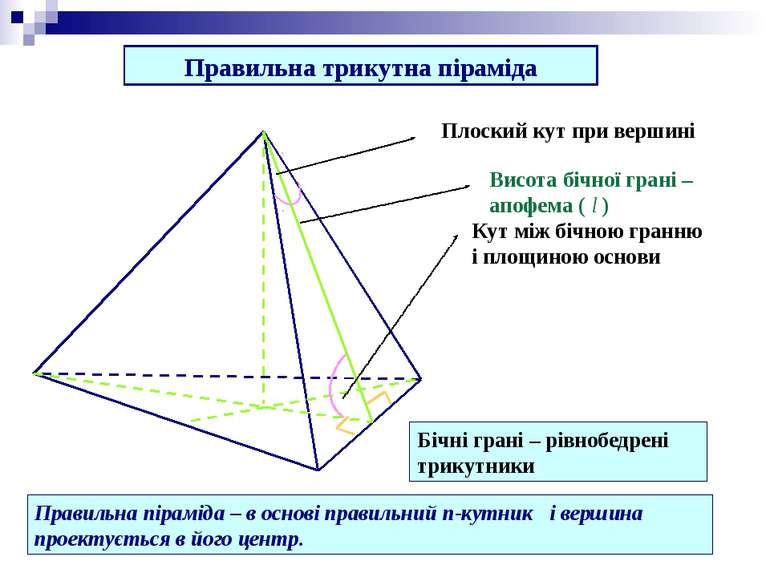
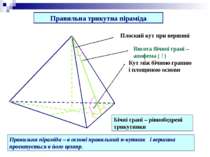
Правильна трикутна піраміда Висота бічної грані – апофема ( l ) Кут між бічною гранню і площиною основи Плоский кут при вершині Бічні грані – рівнобедрені трикутники Правильна піраміда – в основі правильний n-кутник і вершина проектується в його центр.

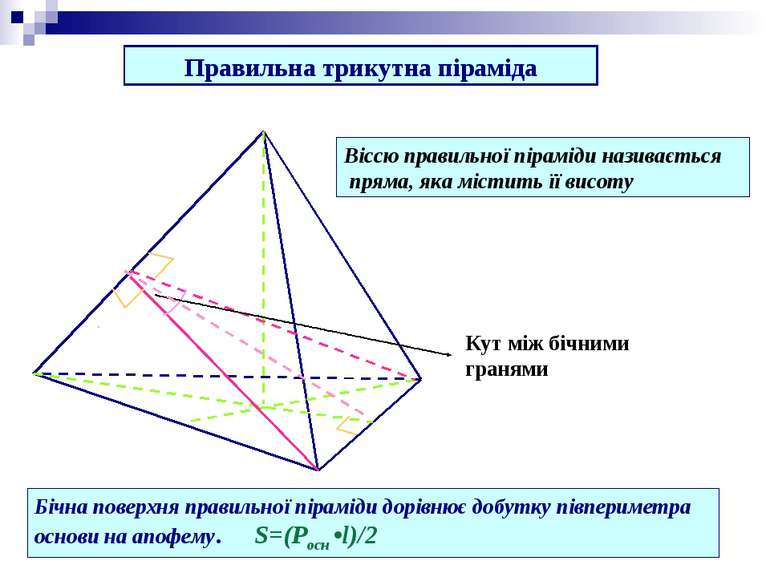
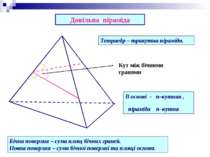
Кут між бічними гранями Бічна поверхня правильної піраміди дорівнює добутку півпериметра основи на апофему. S=(Росн •l)/2 Правильна трикутна піраміда Віссю правильної піраміди називається пряма, яка містить її висоту

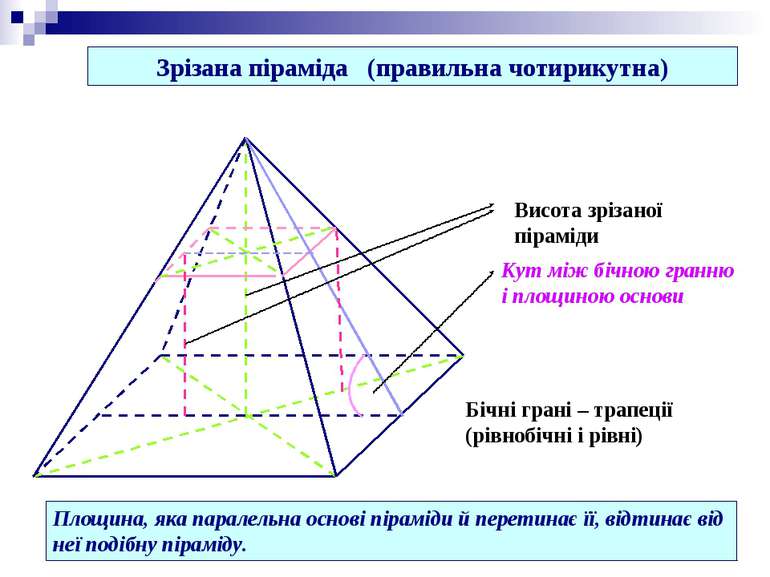
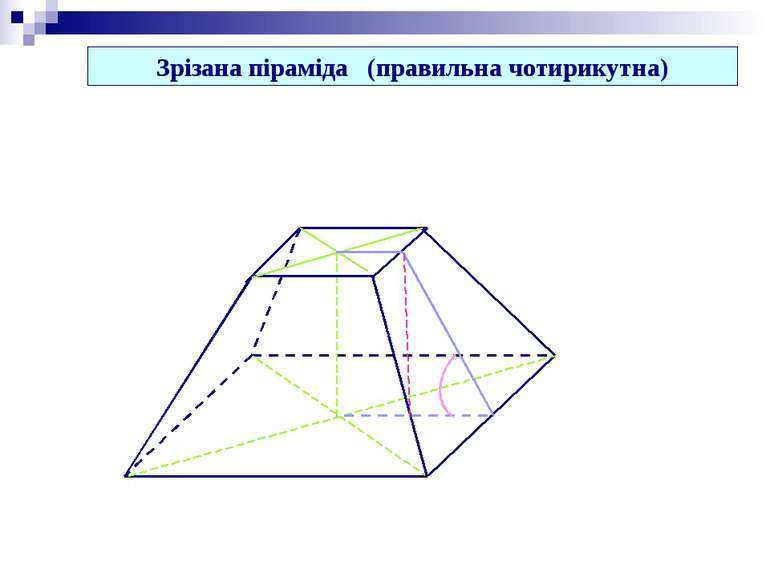
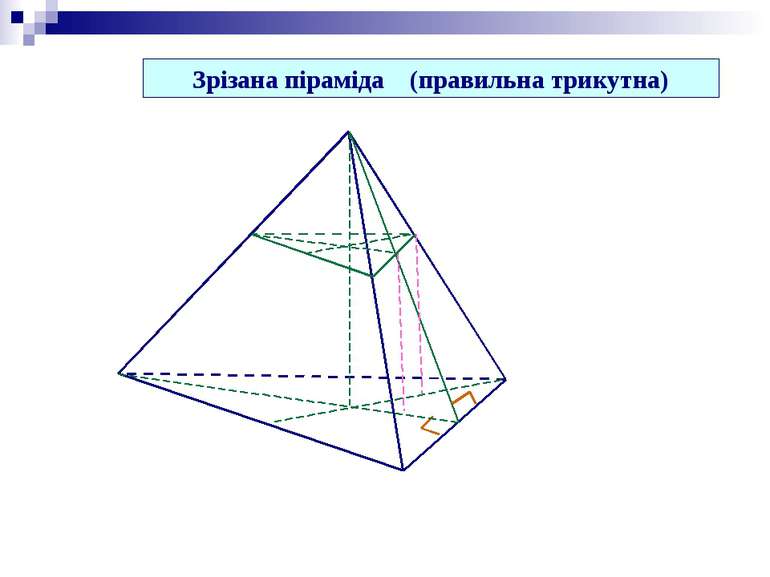
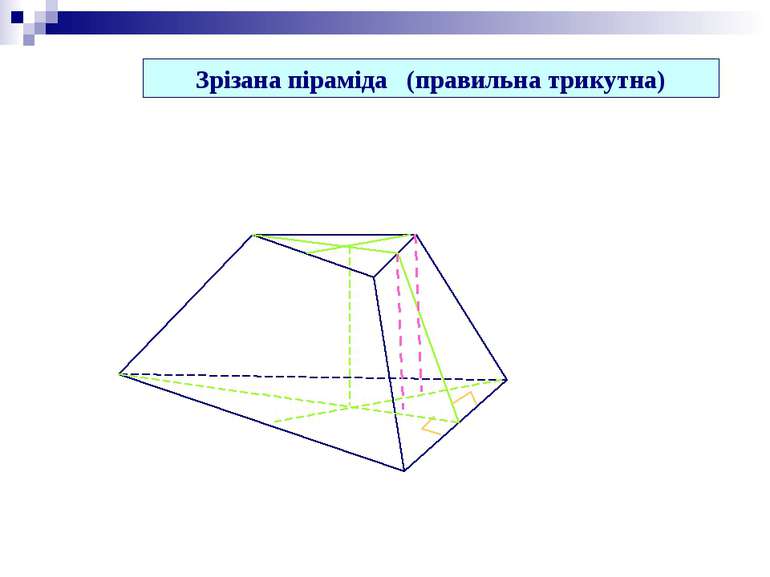
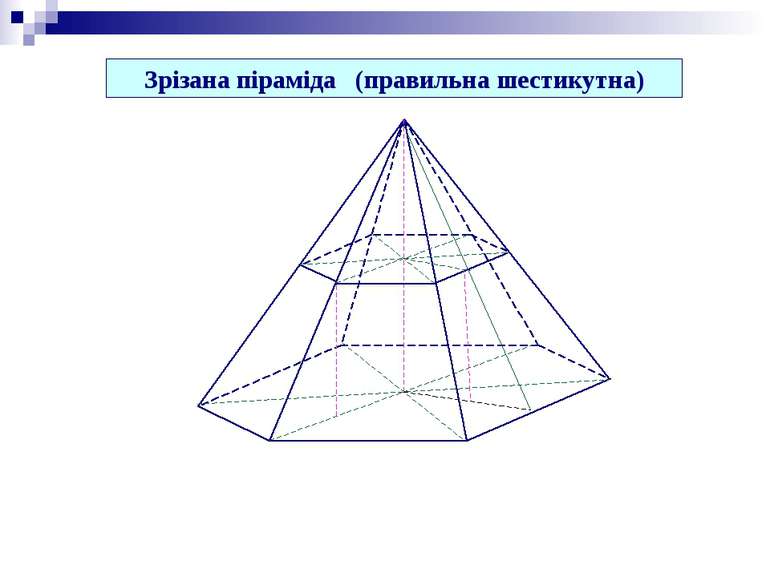
Зрізана піраміда (правильна чотирикутна) Площина, яка паралельна основі піраміди й перетинає її, відтинає від неї подібну піраміду. Висота зрізаної піраміди Кут між бічною гранню і площиною основи Бічні грані – трапеції (рівнобічні і рівні)

Зрізана піраміда (правильна чотирикутна)

Зрізана піраміда (правильна трикутна)

Зрізана піраміда (правильна трикутна)

Зрізана піраміда (правильна шестикутна)

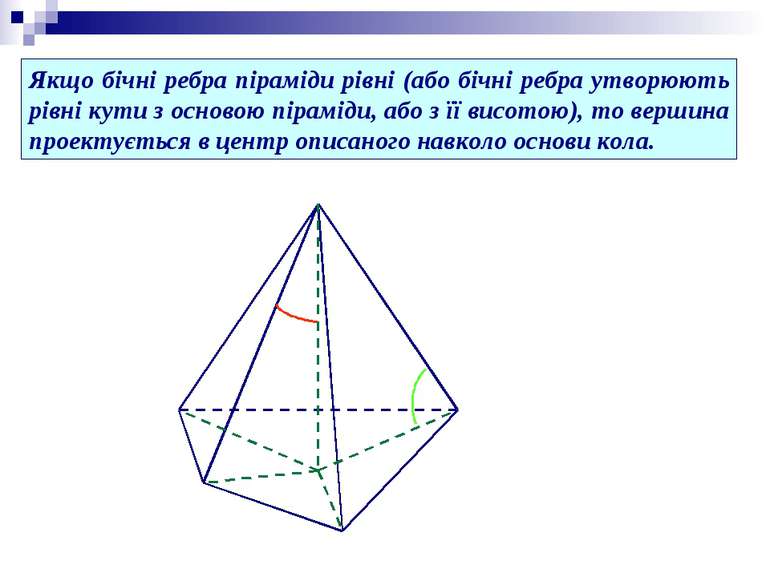
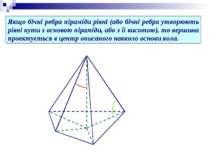
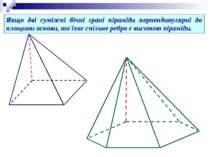
Якщо бічні ребра піраміди рівні (або бічні ребра утворюють рівні кути з основою піраміди, або з її висотою), то вершина проектується в центр описаного навколо основи кола.

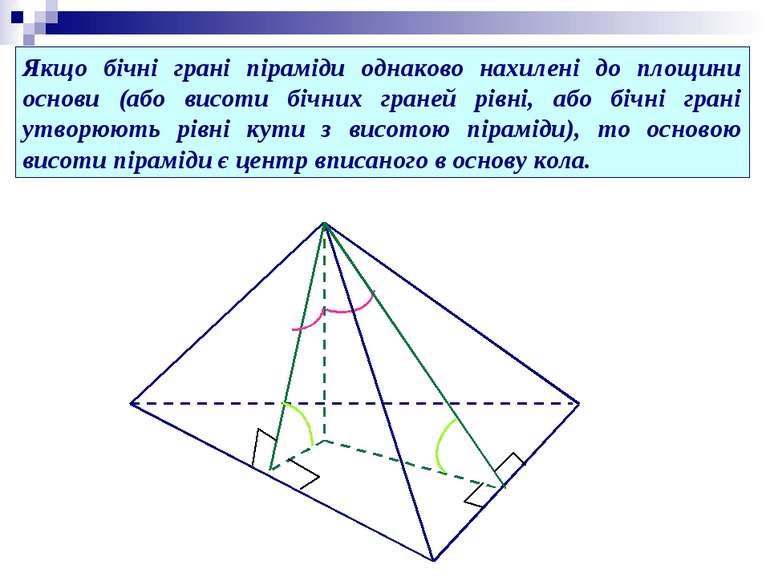
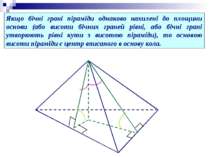
Якщо бічні грані піраміди однаково нахилені до площини основи (або висоти бічних граней рівні, або бічні грані утворюють рівні кути з висотою піраміди), то основою висоти піраміди є центр вписаного в основу кола.

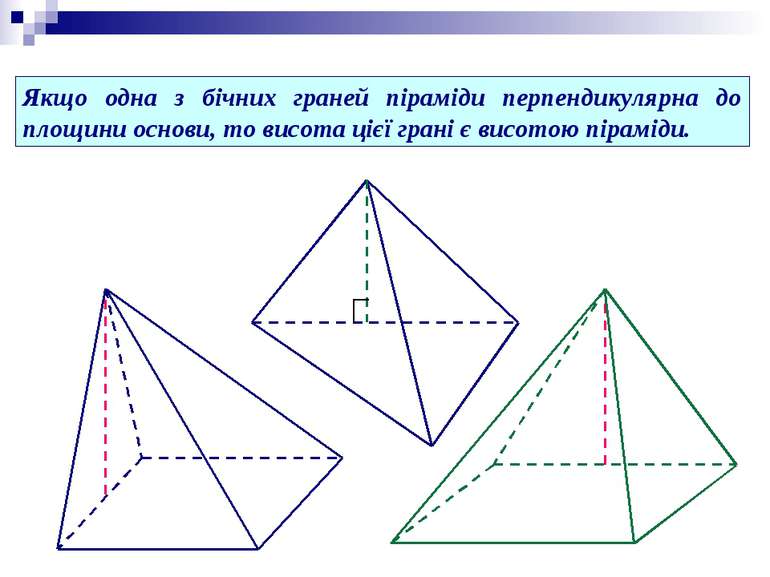
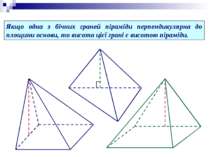
Якщо одна з бічних граней піраміди перпендикулярна до площини основи, то висота цієї грані є висотою піраміди.

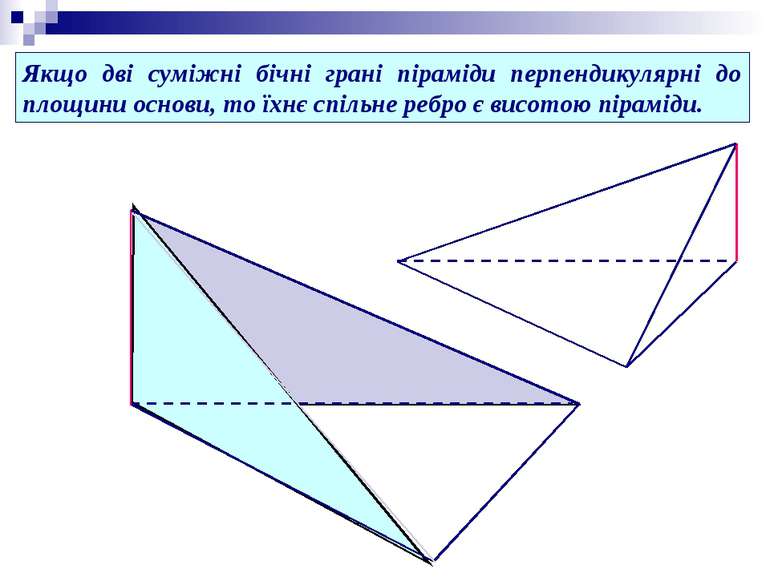
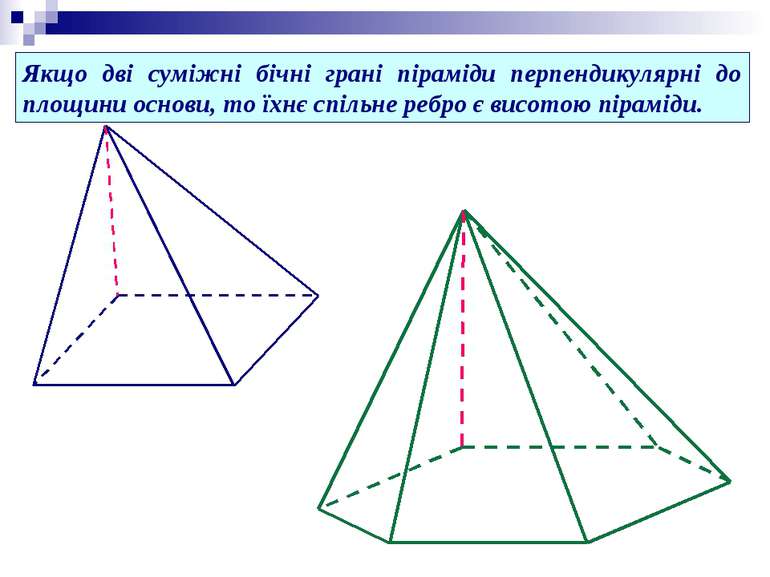
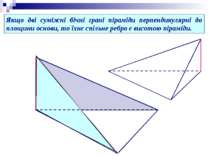
Якщо дві суміжні бічні грані піраміди перпендикулярні до площини основи, то їхнє спільне ребро є висотою піраміди.

Якщо дві суміжні бічні грані піраміди перпендикулярні до площини основи, то їхнє спільне ребро є висотою піраміди.

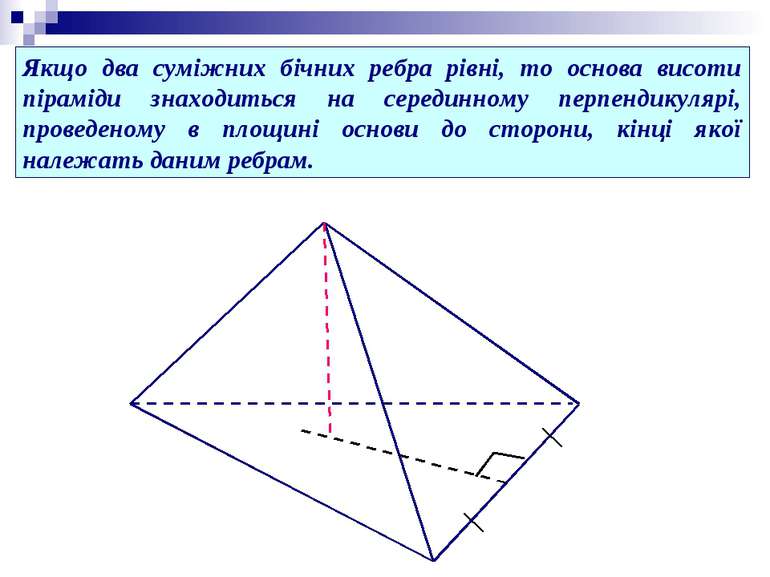
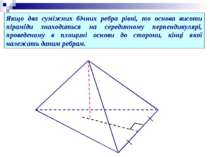
Якщо два суміжних бічних ребра рівні, то основа висоти піраміди знаходиться на серединному перпендикулярі, проведеному в площині основи до сторони, кінці якої належать даним ребрам.

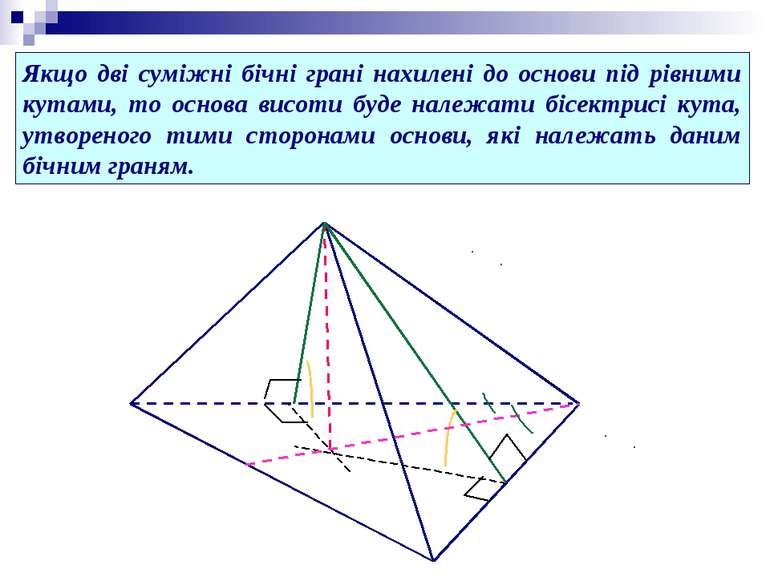
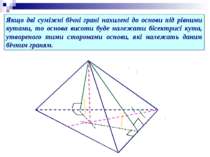
Якщо дві суміжні бічні грані нахилені до основи під рівними кутами, то основа висоти буде належати бісектрисі кута, утвореного тими сторонами основи, які належать даним бічним граням.