Презентація на тему:
Поняття про ЧОТИРИКУТНИКИ

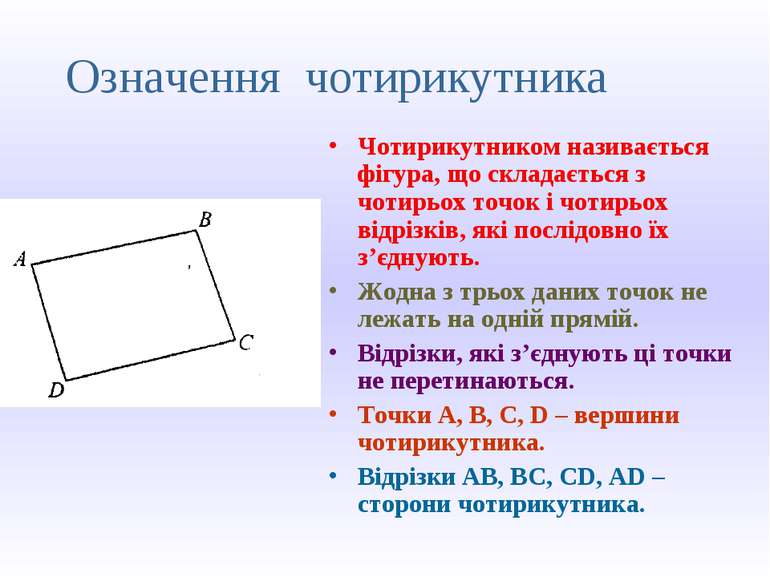
Означення чотирикутника Чотирикутником називається фігура, що складається з чотирьох точок і чотирьох відрізків, які послідовно їх з’єднують. Жодна з трьох даних точок не лежать на одній прямій. Відрізки, які з’єднують ці точки не перетинаються. Точки A, B, C, D – вершини чотирикутника. Відрізки AB, BC, CD, AD – сторони чотирикутника.

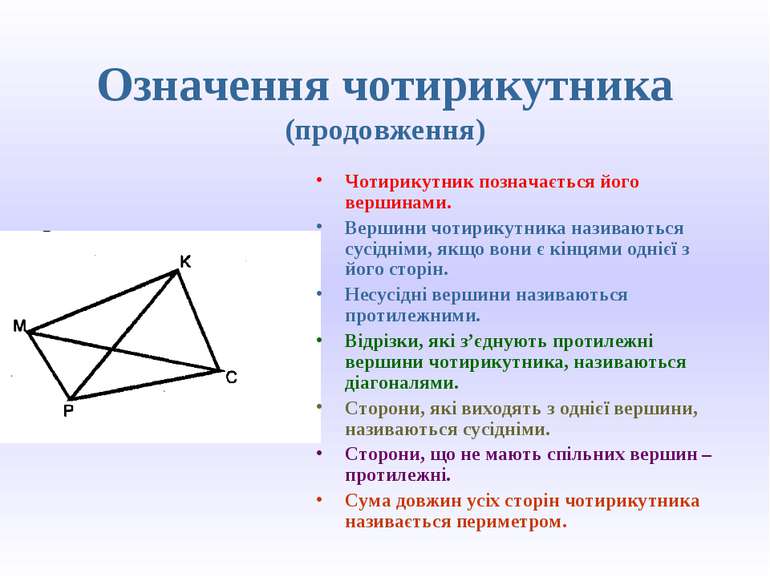
Означення чотирикутника (продовження) Чотирикутник позначається його вершинами. Вершини чотирикутника називаються сусідніми, якщо вони є кінцями однієї з його сторін. Несусідні вершини називаються протилежними. Відрізки, які з’єднують протилежні вершини чотирикутника, називаються діагоналями. Сторони, які виходять з однієї вершини, називаються сусідніми. Сторони, що не мають спільних вершин – протилежні. Сума довжин усіх сторін чотирикутника називається периметром.

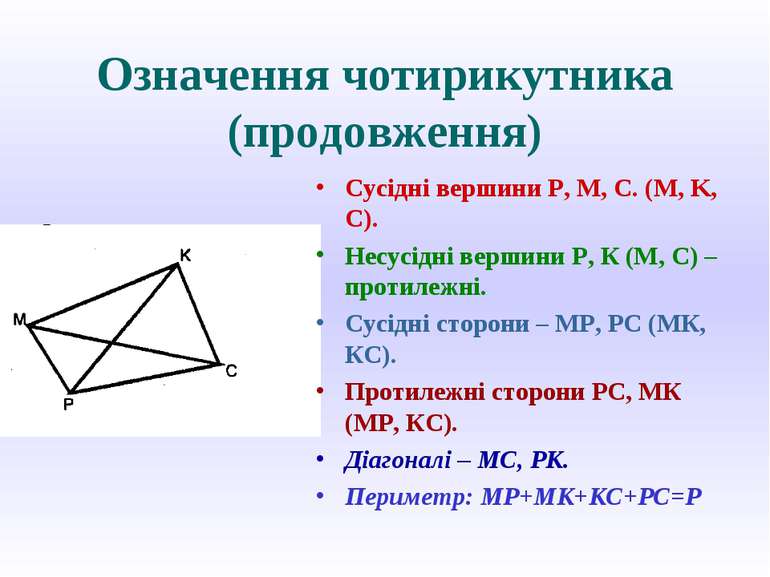
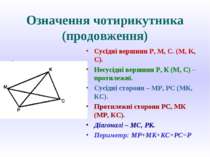
Означення чотирикутника (продовження) Сусідні вершини P, M, C. (M, K, C). Несусідні вершини Р, К (М, С) – протилежні. Сусідні сторони – МР, РС (МК, КС). Протилежні сторони РС, МК (МР, КС). Діагоналі – МС, РК. Периметр: МР+МК+КС+РС=Р

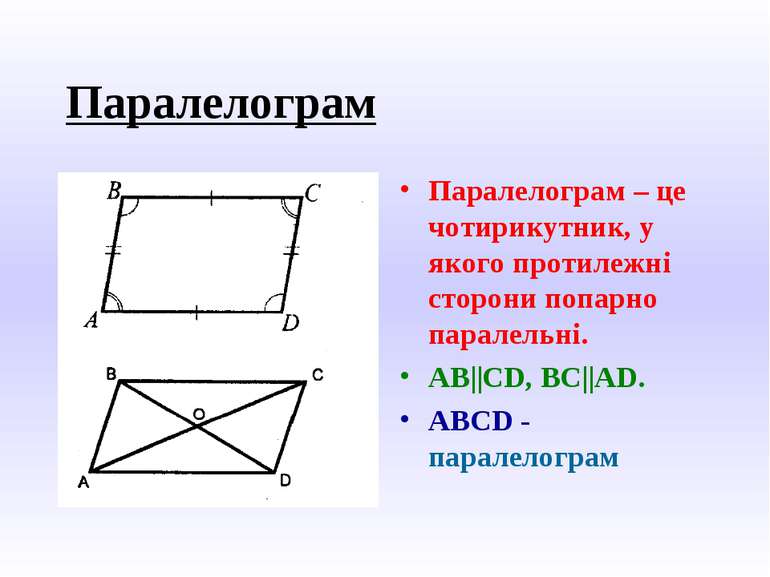
Паралелограм Паралелограм – це чотирикутник, у якого протилежні сторони попарно паралельні. AB||CD, BC||AD. ABCD - паралелограм

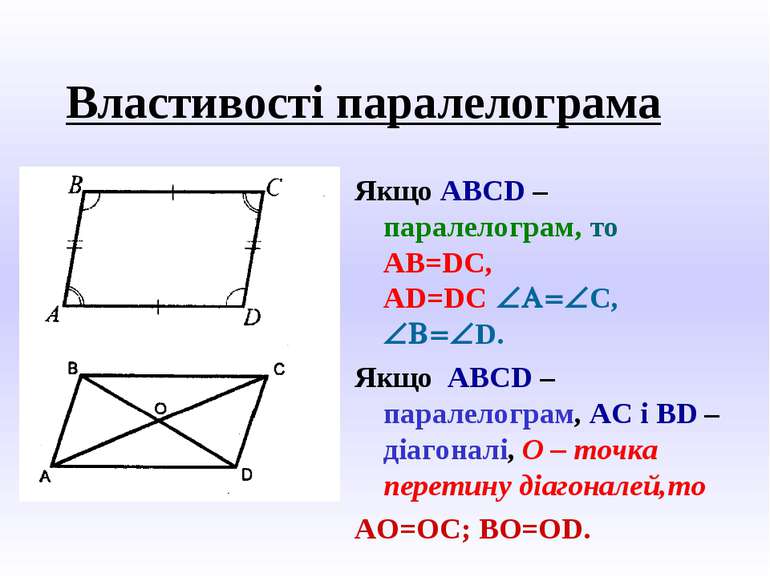
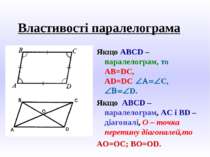
Властивості паралелограма Якщо ABCD – паралелограм, то AB=DC, AD=DC ÐA=ÐC, ÐB=ÐD. Якщо ABCD – паралелограм, AC i BD – діагоналі, О – точка перетину діагоналей,то АО=ОС; ВО=OD.

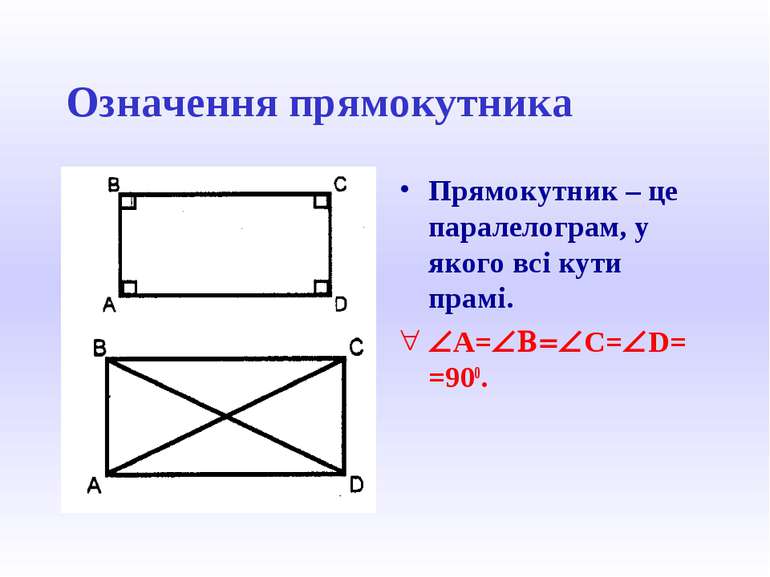
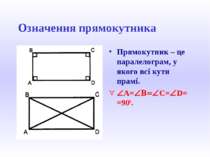
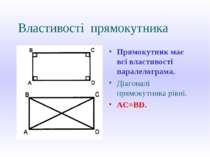
Означення прямокутника Прямокутник – це паралелограм, у якого всі кути прамі. ÐA=ÐB=ÐC=ÐD= =900.

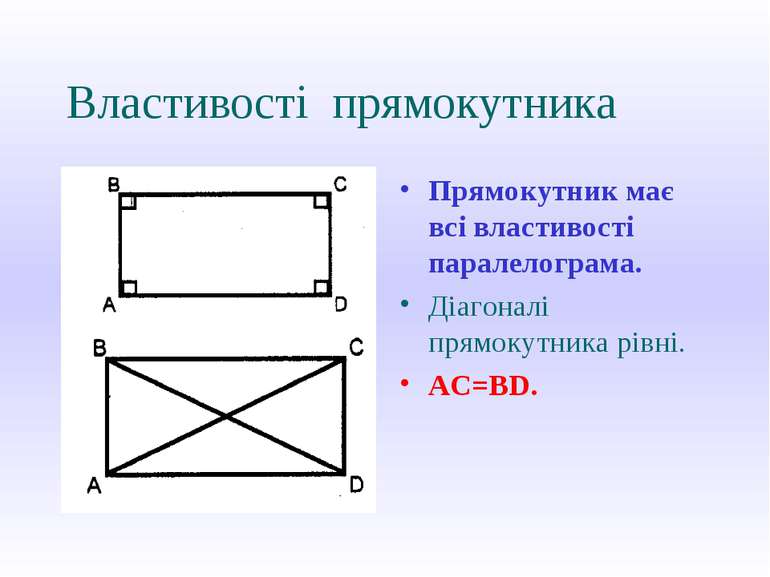
Властивості прямокутника Прямокутник має всі властивості паралелограма. Діагоналі прямокутника рівні. AC=BD.

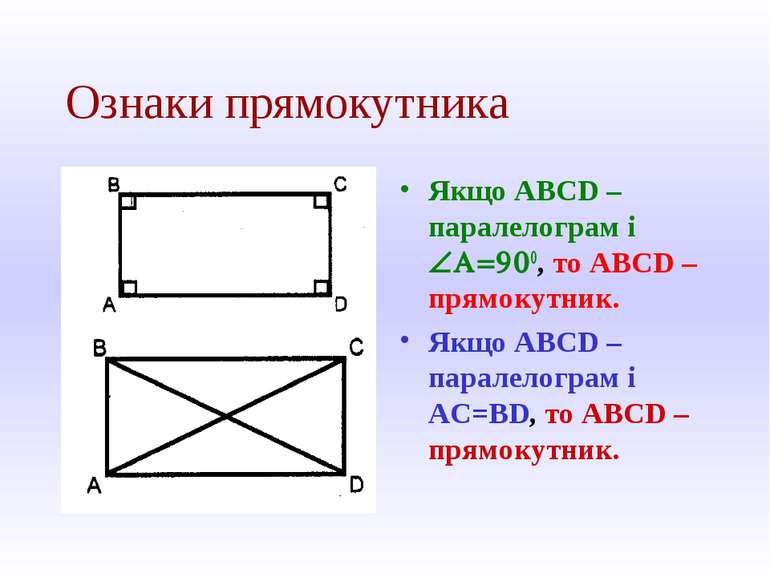
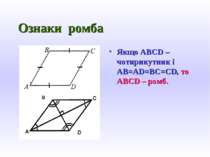
Ознаки прямокутника Якщо ABCD – паралелограм і ÐA=900, то ABCD – прямокутник. Якщо ABCD – паралелограм і АС=BD, то ABCD – прямокутник.

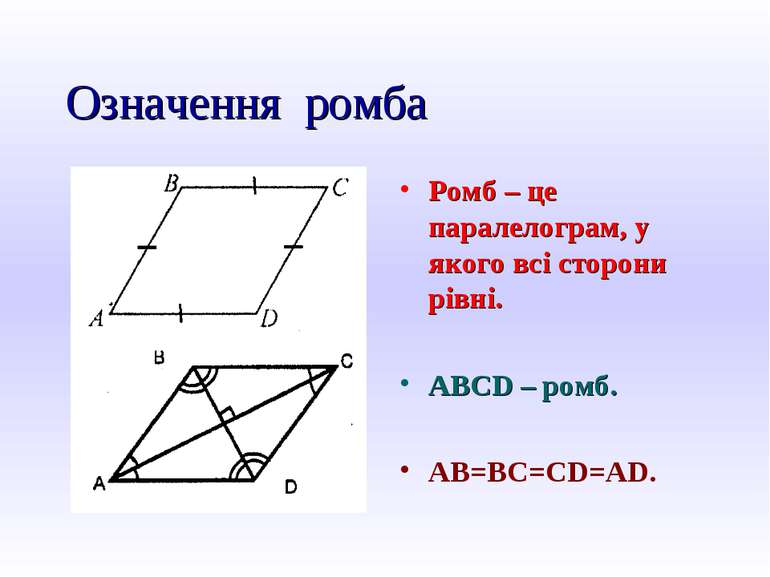
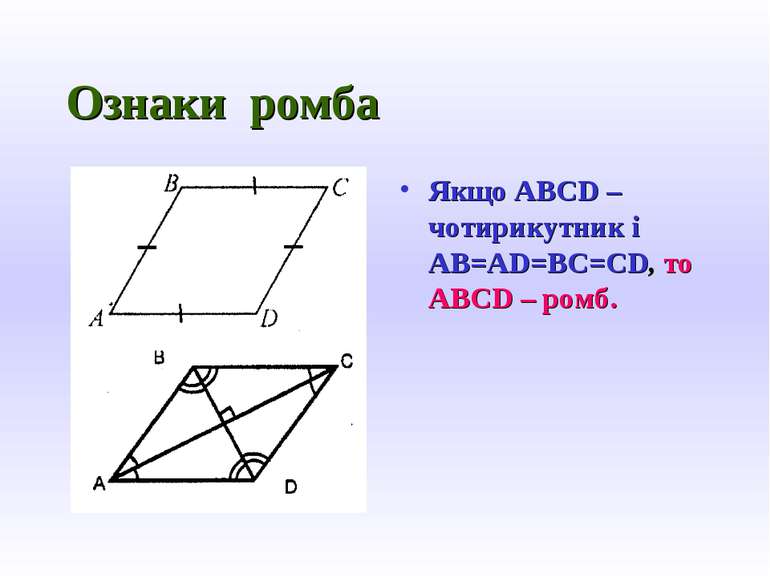
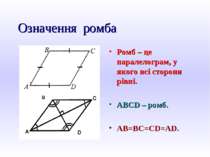
Означення ромба Ромб – це паралелограм, у якого всі сторони рівні. ABCD – ромб. AB=BC=CD=AD.

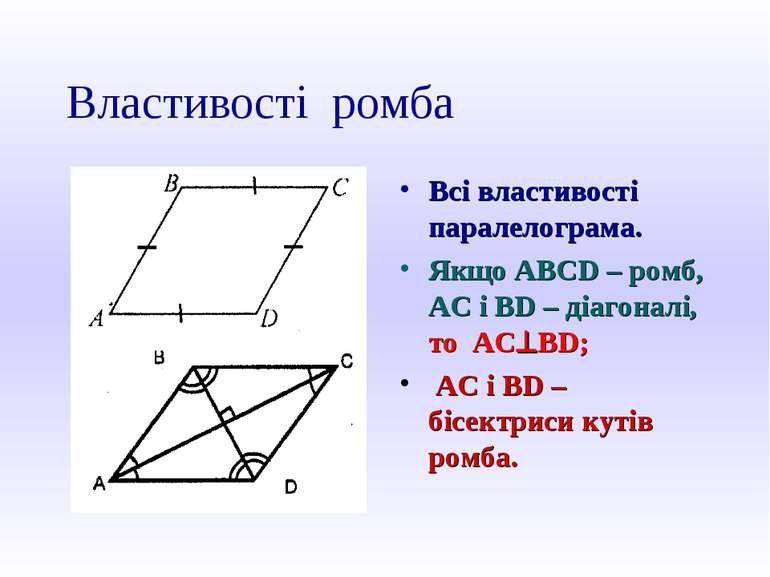
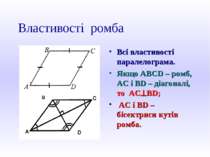
Властивості ромба Всі властивості паралелограма. Якщо ABCD – ромб, АС і BD – діагоналі, то AC^BD; AC i BD – бісектриси кутів ромба.

Ознаки ромба Якщо ABCD – чотирикутник і AB=AD=BC=CD, то ABCD – ромб.

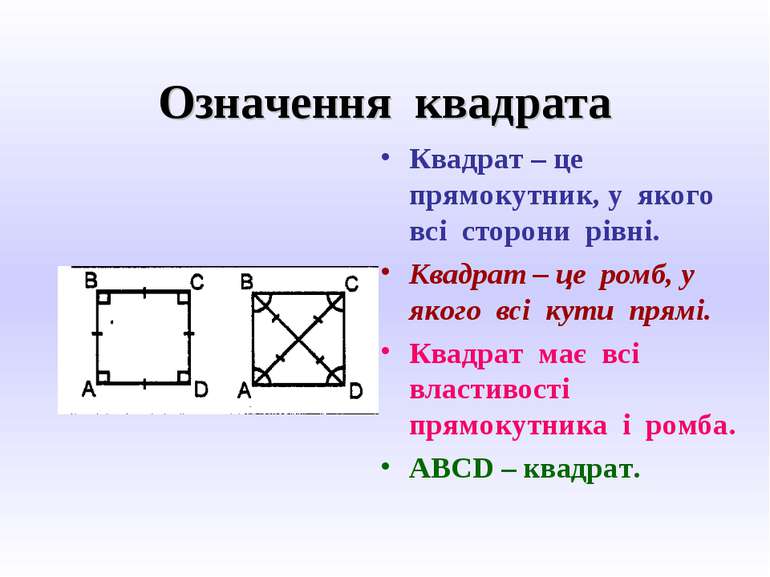
Означення квадрата Квадрат – це прямокутник, у якого всі сторони рівні. Квадрат – це ромб, у якого всі кути прямі. Квадрат має всі властивості прямокутника і ромба. ABCD – квадрат.

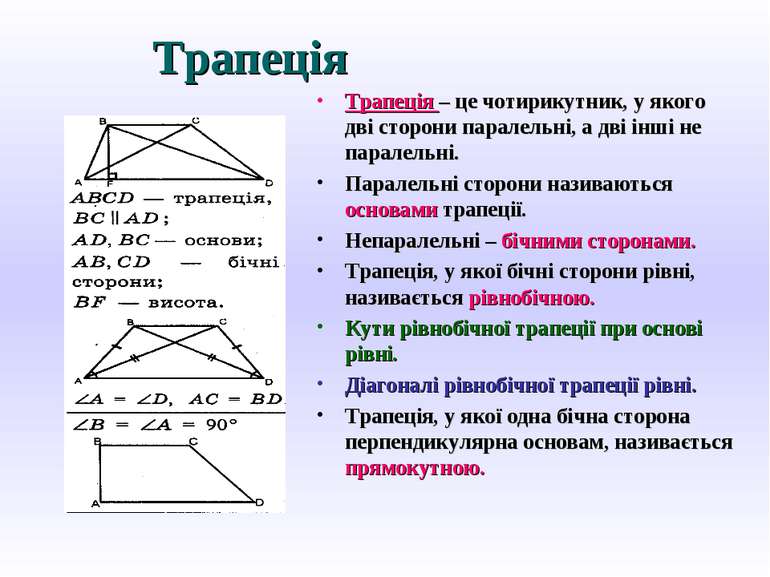
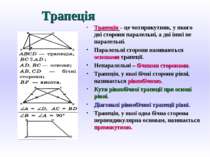
Трапеція Трапеція – це чотирикутник, у якого дві сторони паралельні, а дві інші не паралельні. Паралельні сторони називаються основами трапеції. Непаралельні – бічними сторонами. Трапеція, у якої бічні сторони рівні, називається рівнобічною. Кути рівнобічної трапеції при основі рівні. Діагоналі рівнобічної трапеції рівні. Трапеція, у якої одна бічна сторона перпендикулярна основам, називається прямокутною.

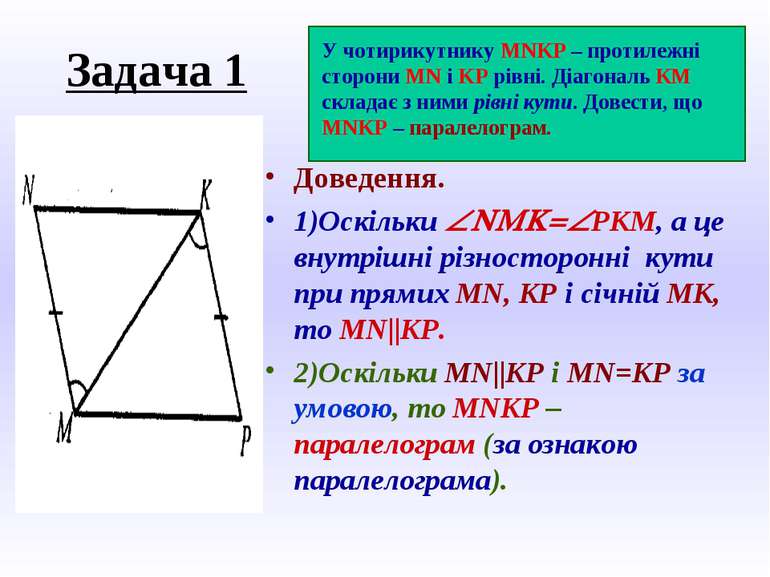
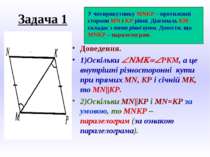
Задача 1 Доведення. 1)Оскільки ÐNMK=ÐРКМ, а це внутрішні різносторонні кути при прямих MN, KP і січній МК, то MN||KP. 2)Оскільки MN||KP i MN=KP за умовою, то MNKP – паралелограм (за ознакою паралелограма). У чотирикутнику MNKP – протилежні сторони MN i KP рівні. Діагональ КМ складає з ними рівні кути. Довести, що MNKP – паралелограм.

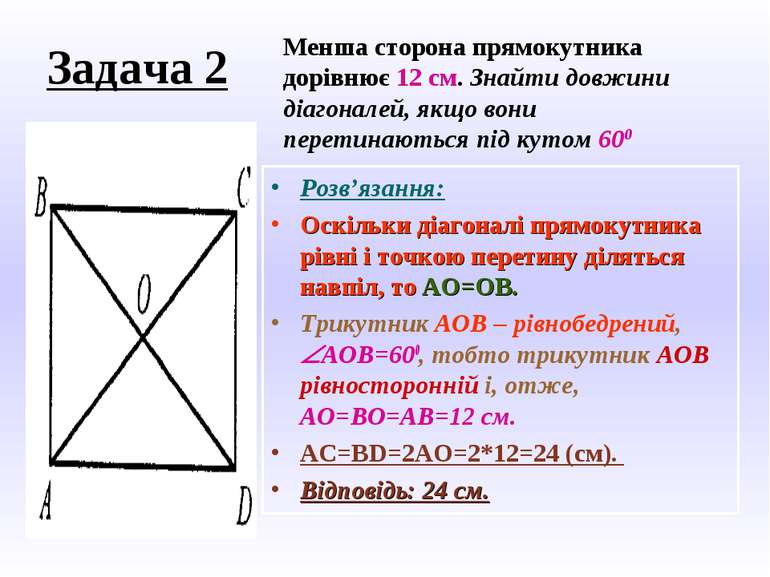
Задача 2 Розв’язання: Оскільки діагоналі прямокутника рівні і точкою перетину діляться навпіл, то АО=ОВ. Трикутник АОВ – рівнобедрений, ÐАОВ=600, тобто трикутник АОВ рівносторонній і, отже, АО=ВО=АВ=12 см. AC=BD=2AO=2*12=24 (cм). Відповідь: 24 см. Менша сторона прямокутника дорівнює 12 см. Знайти довжини діагоналей, якщо вони перетинаються під кутом 600

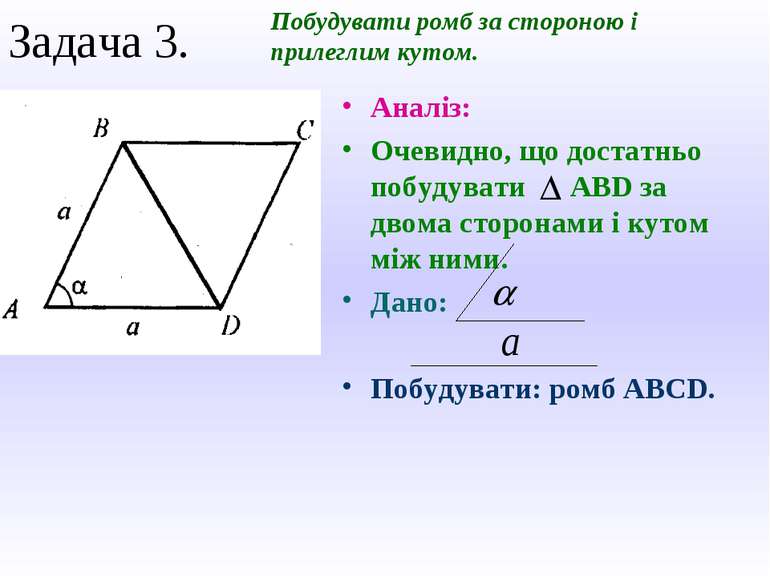
Задача 3. Побудувати ромб за стороною і прилеглим кутом. Аналіз: Очевидно, що достатньо побудувати ABD за двома сторонами і кутом між ними. Дано: Побудувати: ромб ABCD.

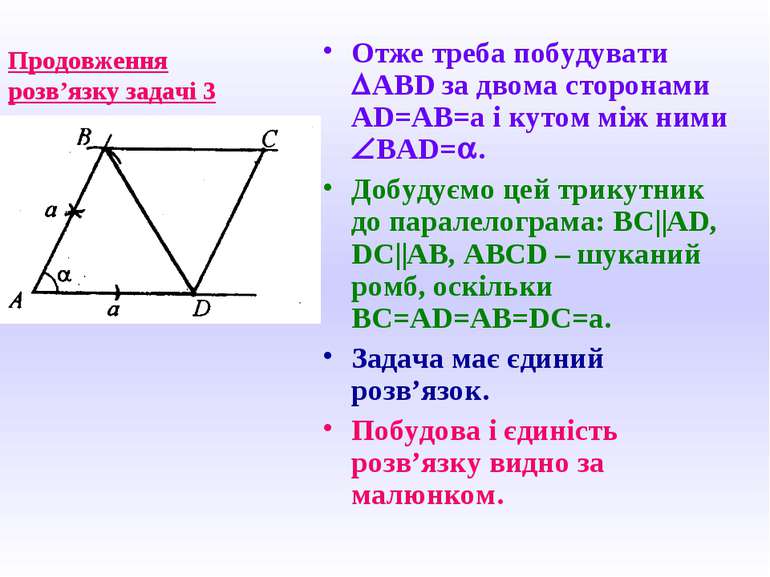
Продовження розв’язку задачі 3 Отже треба побудувати DABD за двома сторонами AD=AB=a і кутом між ними ÐBAD=a. Добудуємо цей трикутник до паралелограма: BC||AD, DC||AB, ABCD – шуканий ромб, оскільки BC=AD=AB=DC=a. Задача має єдиний розв’язок. Побудова і єдиність розв’язку видно за малюнком.

ЗАВДАННЯ ДОДОМУ Повторити п.п. 50 – 56, 59. Запитання 1 – 14, 17. Задачі № 42, 45. Переглянути в зошиті розв’язання задач по темі “Чотирикутники”.