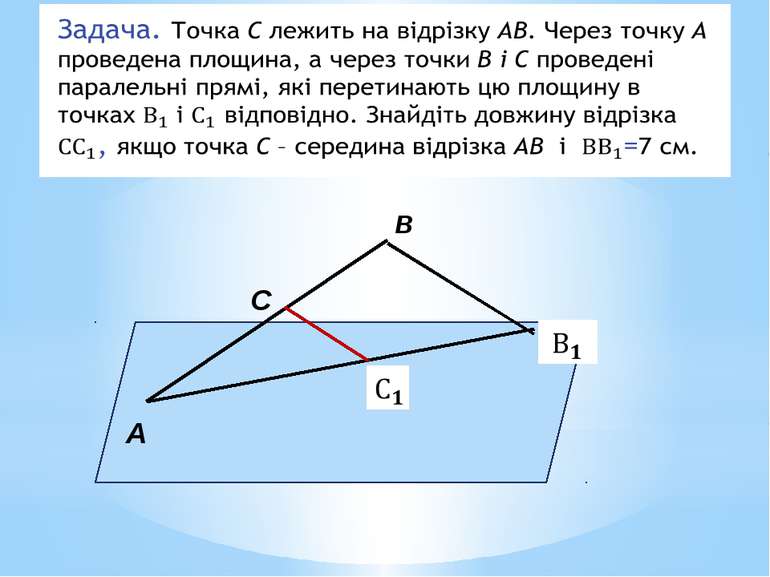
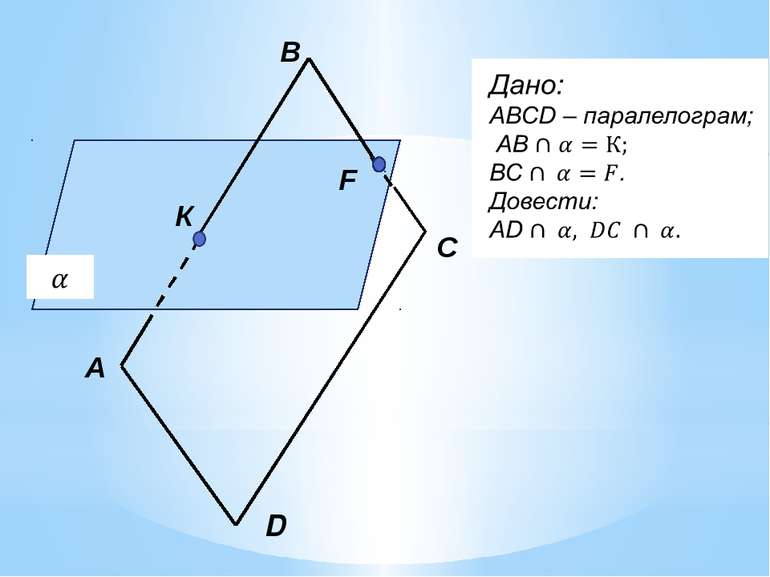
Презентація на тему:
Паралельність прямих та площин у просторі

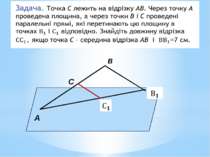
Паралельність прямих та площин у просторі Тема Підготувала викладач математики Маріупольського професійного машинобудівного ліцею Кожухар Т.О.

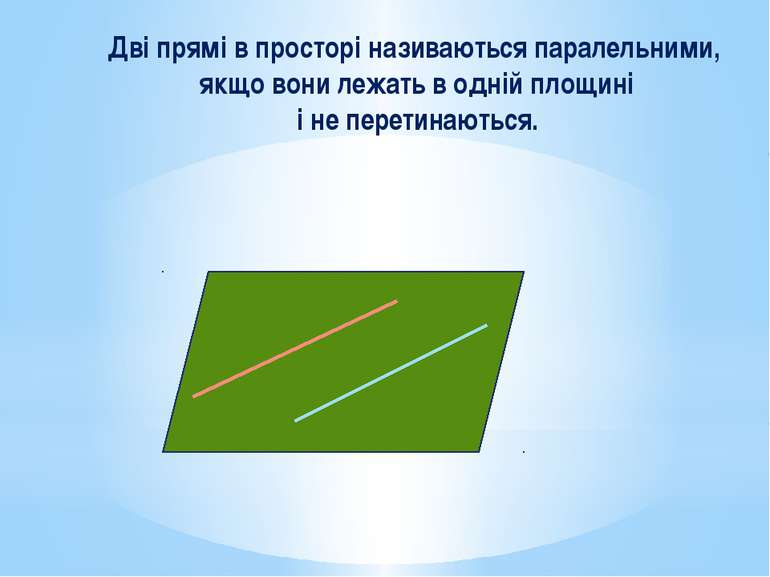
Дві прямі в просторі називаються паралельними, якщо вони лежать в одній площині і не перетинаються.

Приклади паралельних прямих

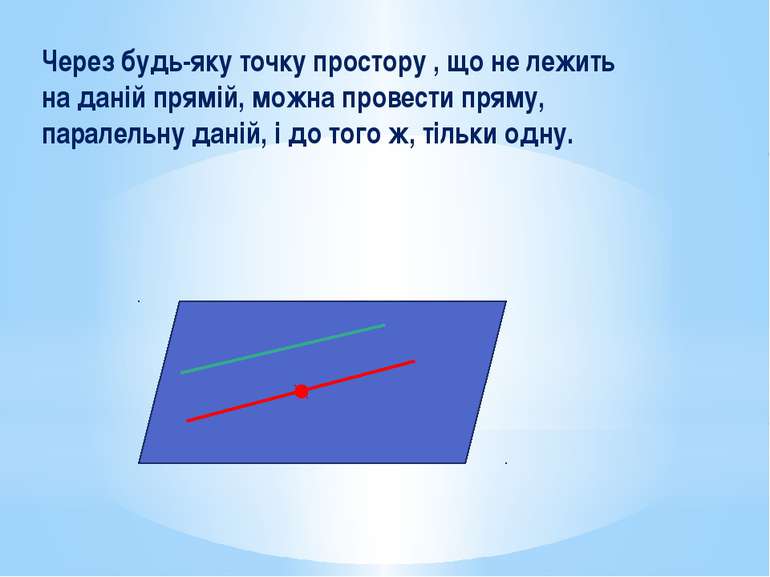
Через будь-яку точку простору , що не лежить на даній прямій, можна провести пряму, паралельну даній, і до того ж, тільки одну.

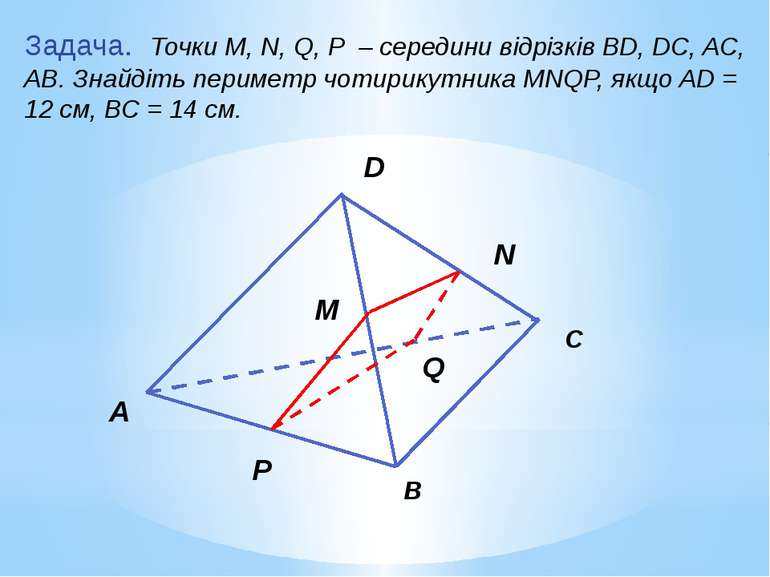
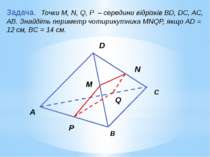
Задача. Точки M, N, Q, P – середини відрізків BD, DC, AC, AB. Знайдіть периметр чотирикутника MNQP, якщо AD = 12 см, ВС = 14 см. D

В С

В

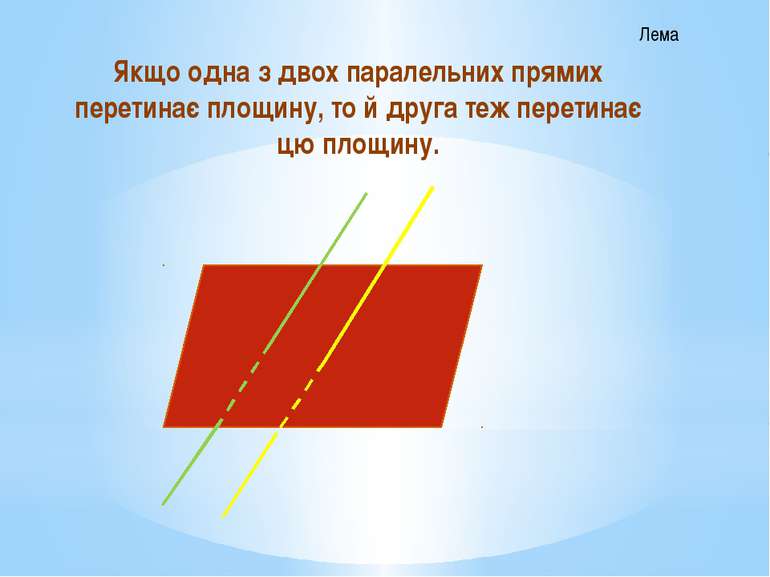
Якщо одна з двох паралельних прямих перетинає площину, то й друга теж перетинає цю площину. Лема

D А В С К F

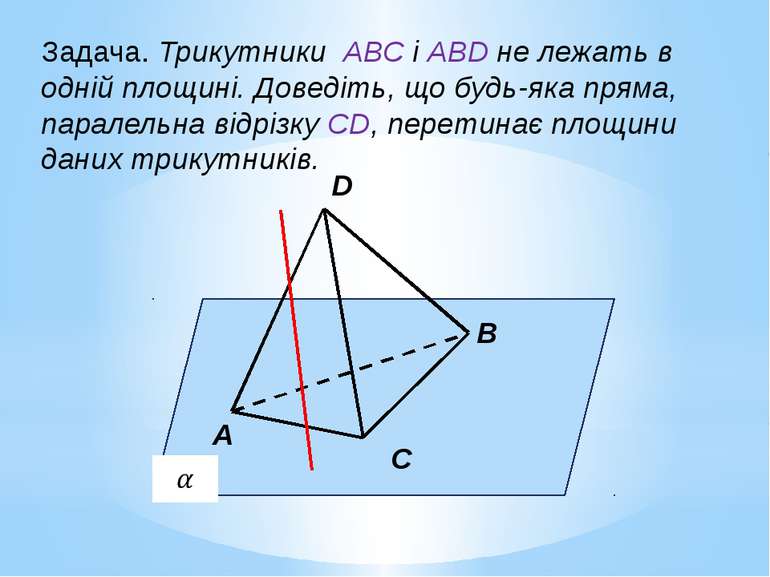
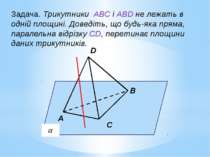
Задача. Трикутники АВС і АВD не лежать в одній площині. Доведіть, що будь-яка пряма, паралельна відрізку СD, перетинає площини даних трикутників. B A C D

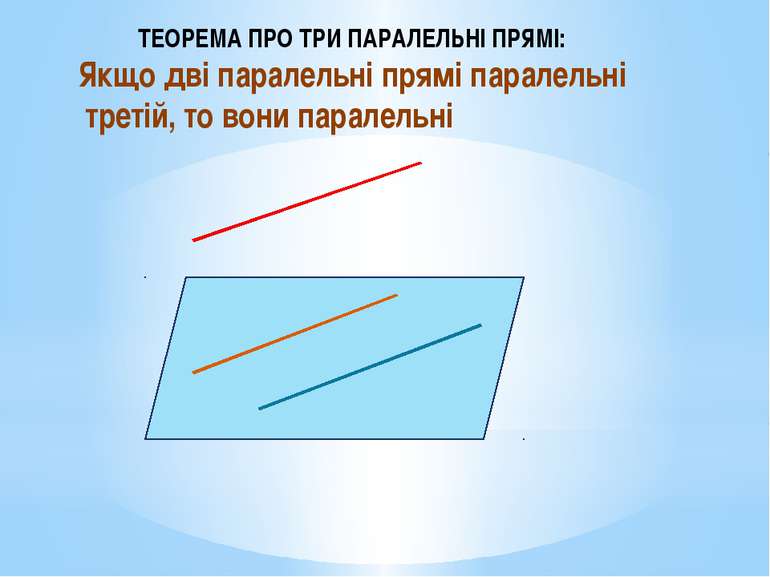
ТЕОРЕМА ПРО ТРИ ПАРАЛЕЛЬНІ ПРЯМІ: Якщо дві паралельні прямі паралельні третій, то вони паралельні

Паралельність прямої і площини

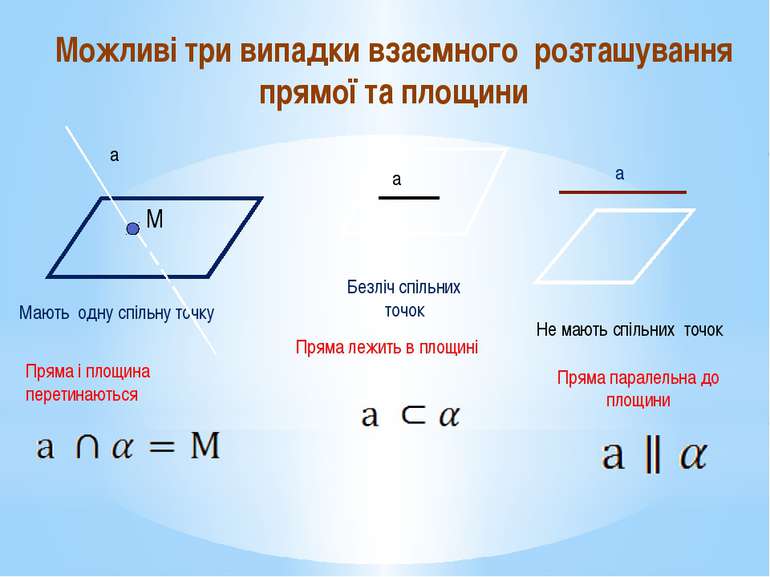
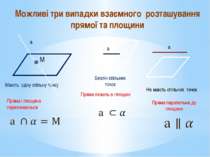
Мають одну спільну точку Безліч спільних точок α а а α а α Пряма паралельна до площини Можливі три випадки взаємного розташування прямої та площини Пряма лежить в площині Пряма і площина перетинаються Не мають спільних точок М

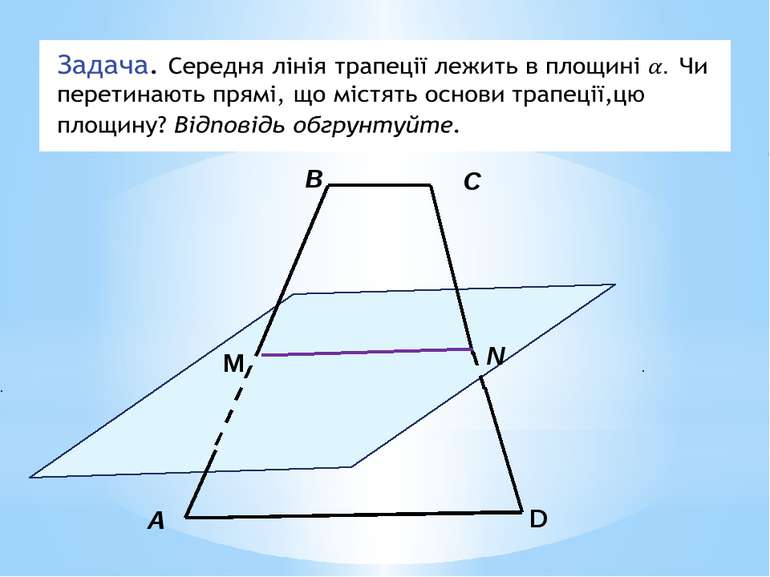
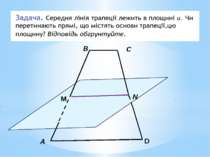
Пряма і площина називаються паралельними якщо вони не мають спільних точок. Лінія перетину стіни і стелі паралельна площині підлоги. В площині підлоги є лінія, паралельна лінії перетину стіни і стелі.

Приклади паралельності прямої та площини

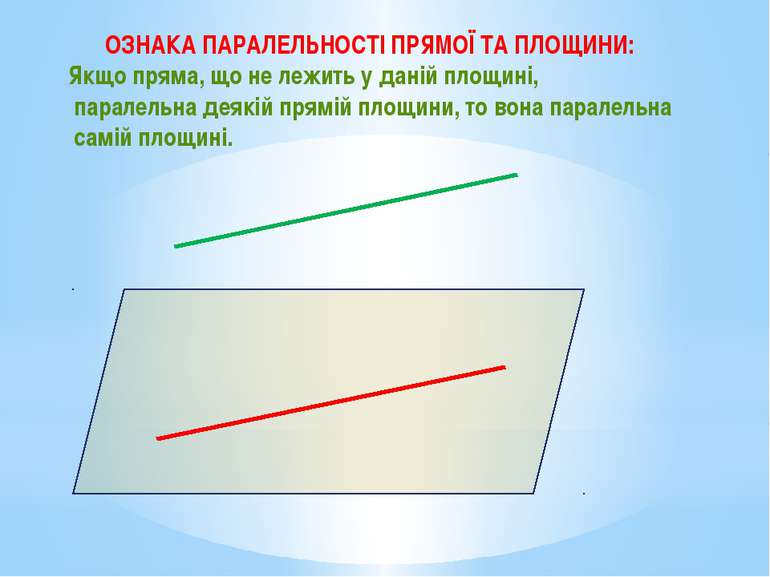
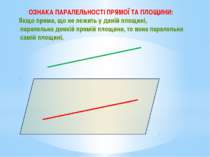
ОЗНАКА ПАРАЛЕЛЬНОСТІ ПРЯМОЇ ТА ПЛОЩИНИ: Якщо пряма, що не лежить у даній площині, паралельна деякій прямій площини, то вона паралельна самій площині.

ВОНА ПАРАЛЕЛЬНА І САМІЙ ПЛОЩИНІ Якщо пряма , яка не лежить у даній площині, паралельна деякій прямій площини, то … Закінчіть речення

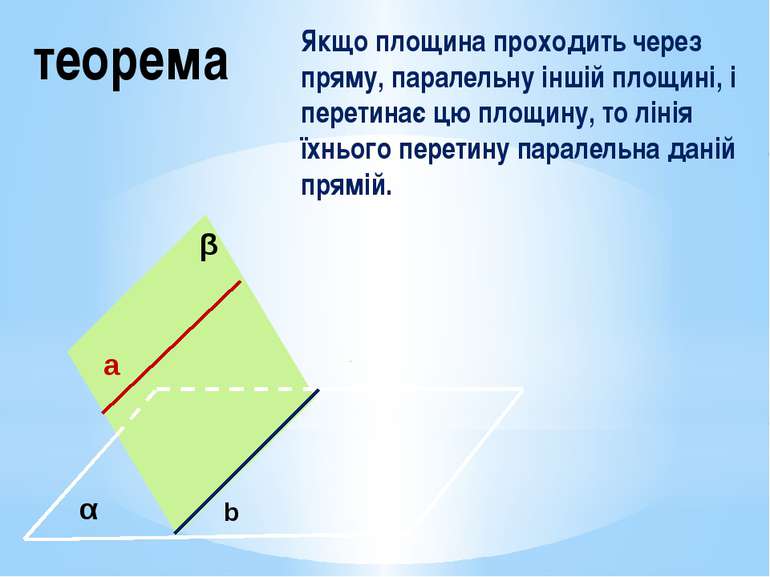
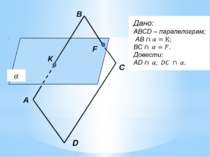
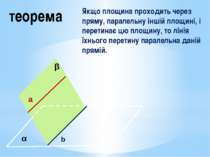
теорема Якщо площина проходить через пряму, паралельну іншій площині, і перетинає цю площину, то лінія їхнього перетину паралельна даній прямій. α β a b

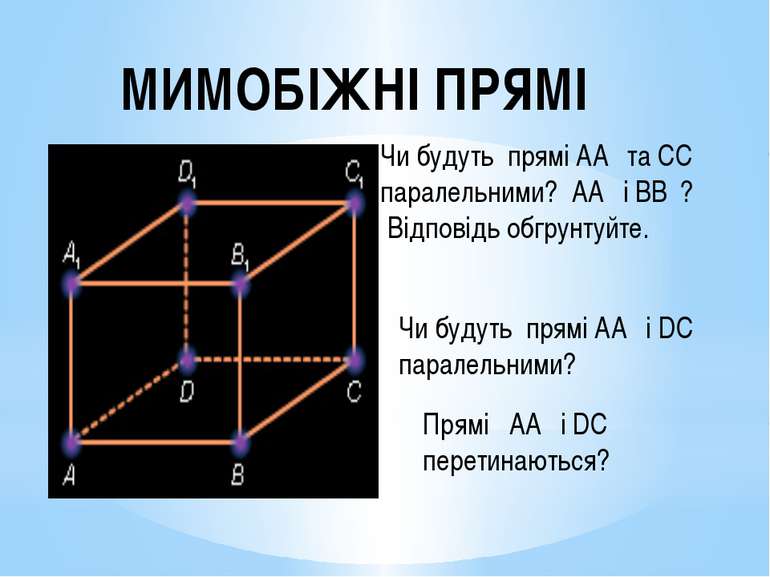
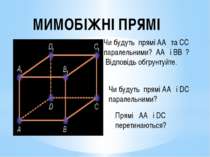
МИМОБІЖНІ ПРЯМІ Чи будуть прямі АА₁ та СС₁ паралельними? АА₁ і ВВ₁? Відповідь обгрунтуйте. Чи будуть прямі АА₁ і DС паралельними? Прямі АА₁ і DС перетинаються?

Які прямі ви бачите на цьому малюнку?

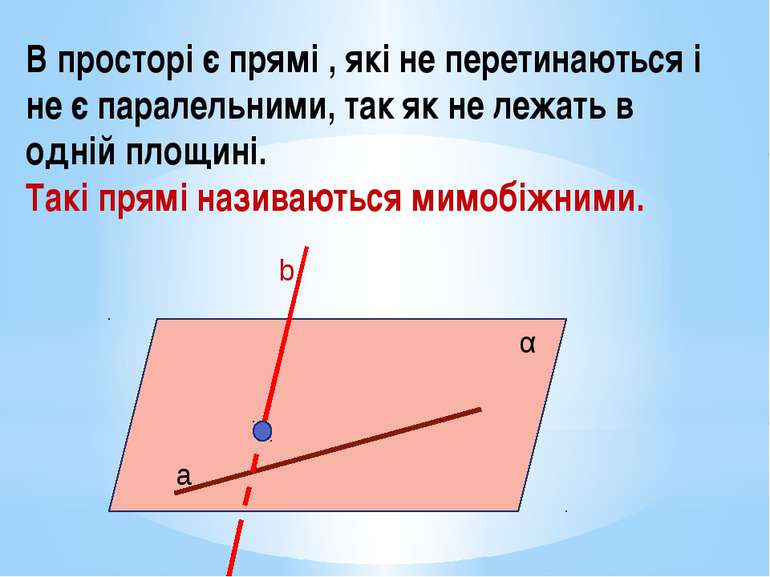
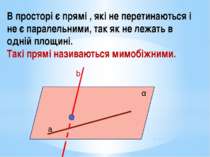
В просторі є прямі , які не перетинаються і не є паралельними, так як не лежать в одній площині. Такі прямі називаються мимобіжними. а b α

Приклади мимобіжних прямих

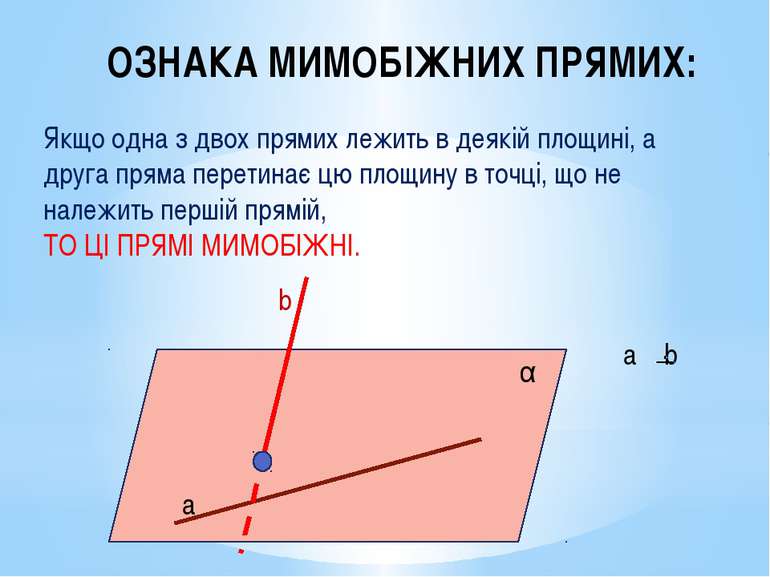
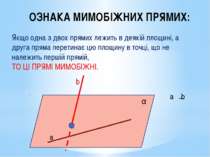
ОЗНАКА МИМОБІЖНИХ ПРЯМИХ: Якщо одна з двох прямих лежить в деякій площині, а друга пряма перетинає цю площину в точці, що не належить першій прямій, ТО ЦІ ПРЯМІ МИМОБІЖНІ. а b α a b

Точка М не лежить в площині чотирикутника АВСD. Яке взаємне розташування прямих МВ і АD ? М А В С D М И М О Б І Ж Н І

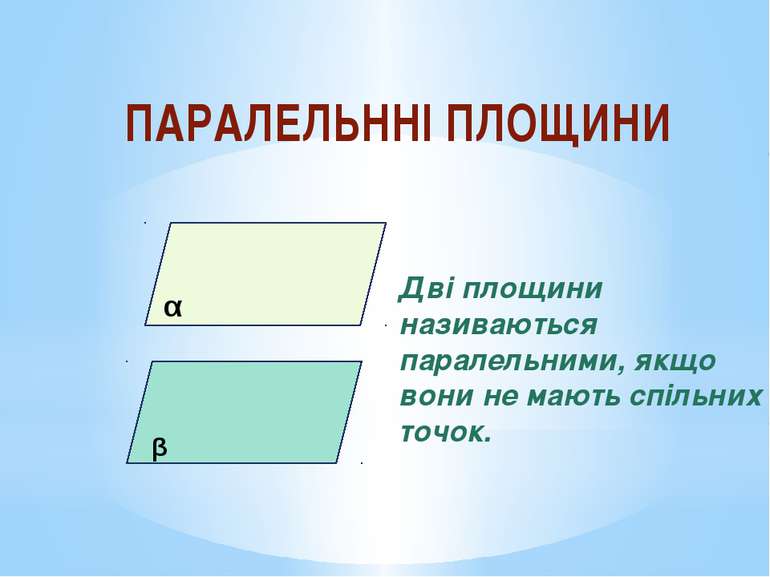
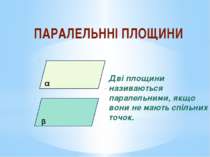
ПАРАЛЕЛЬННІ ПЛОЩИНИ α β Дві площини називаються паралельними, якщо вони не мають спільних точок.

Приклади паралельних площин

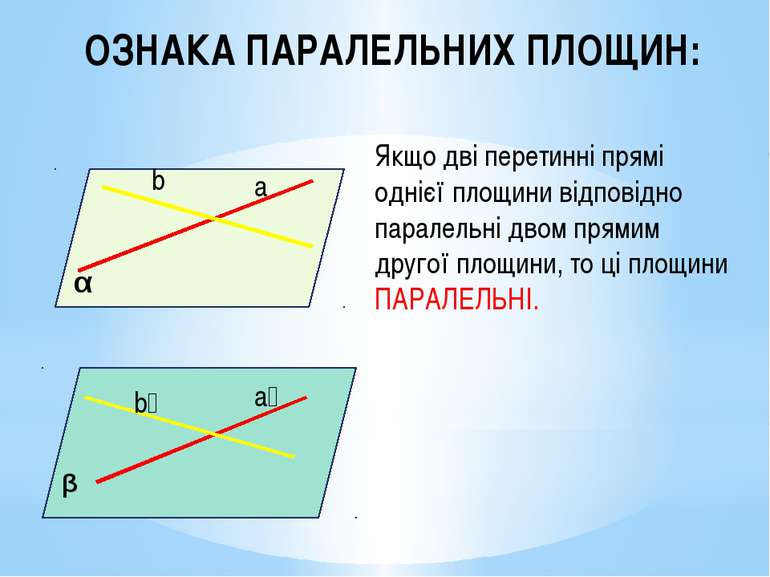
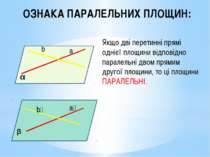
ОЗНАКА ПАРАЛЕЛЬНИХ ПЛОЩИН: Якщо дві перетинні прямі однієї площини відповідно паралельні двом прямим другої площини, то ці площини ПАРАЛЕЛЬНІ. α β a a₁ b₁ b

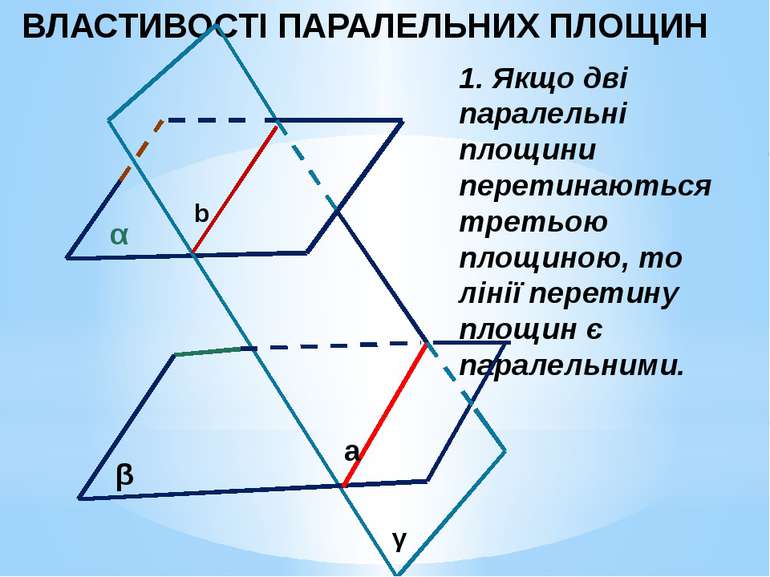
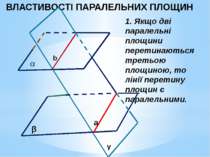
ВЛАСТИВОСТІ ПАРАЛЕЛЬНИХ ПЛОЩИН 1. Якщо дві паралельні площини перетинаються третьою площиною, то лінії перетину площин є паралельними.

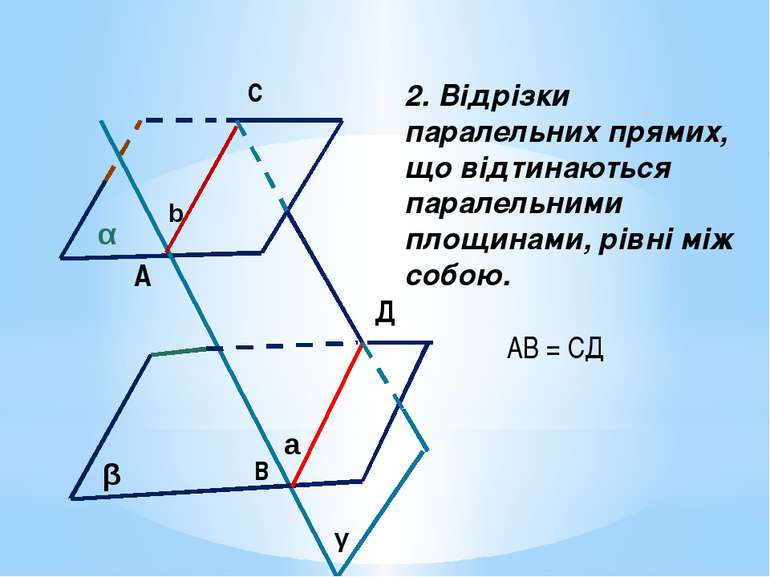
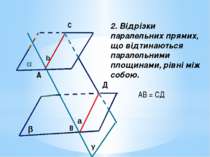
2. Відрізки паралельних прямих, що відтинаються паралельними площинами, рівні між собою. А В С Д АВ = СД α β γ b a

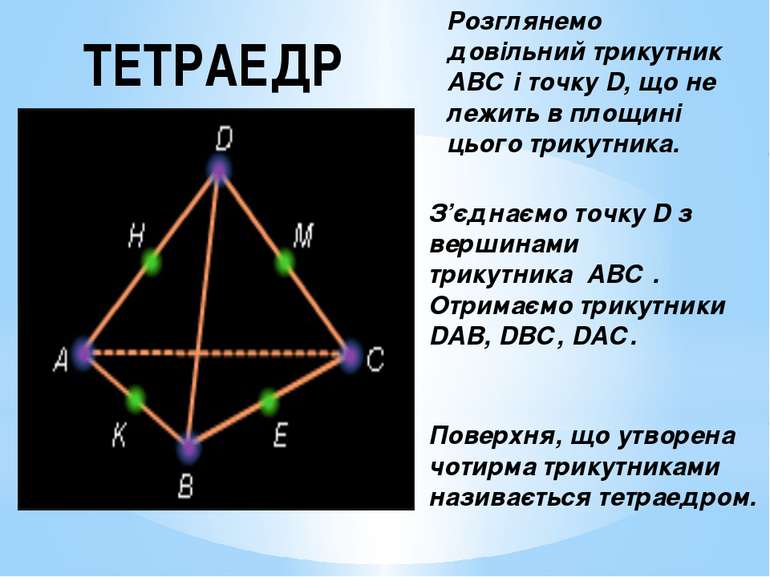
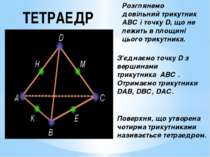
ТЕТРАЕДР Розглянемо довільний трикутник АВС і точку D, що не лежить в площині цього трикутника. З’єднаємо точку D з вершинами трикутника АВС . Отримаємо трикутники DАВ, DВС, DАС. Поверхня, що утворена чотирма трикутниками називається тетраедром.

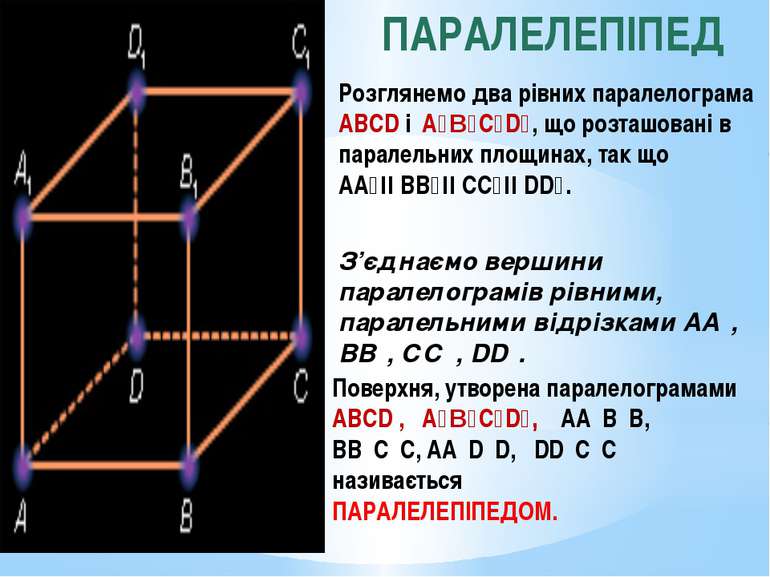
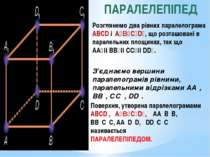
ПАРАЛЕЛЕПІПЕД Розглянемо два рівних паралелограма ABCD і A₁B₁C₁D₁, що розташовані в паралельних площинах, так що AA₁ІІ BB₁ІІ CC₁ІІ DD₁. З’єднаємо вершини паралелограмів рівними, паралельними відрізками АА₁, ВВ₁, СС₁, DD₁. Поверхня, утворена паралелограмами ABCD , A₁B₁C₁D₁, АА₁В₁В, ВВ₁С₁С, АА₁D₁D, DD₁C₁C називається ПАРАЛЕЛЕПІПЕДОМ.

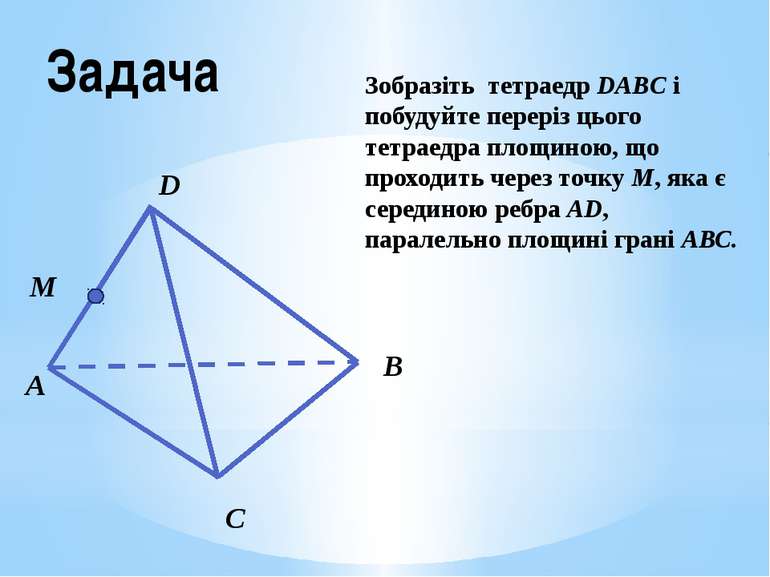
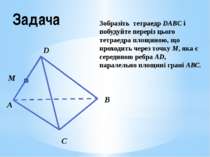
Задача Зобразіть тетраедр DABC і побудуйте переріз цього тетраедра площиною, що проходить через точку М, яка є серединою ребра AD, паралельно площині грані АВС. С В А D М

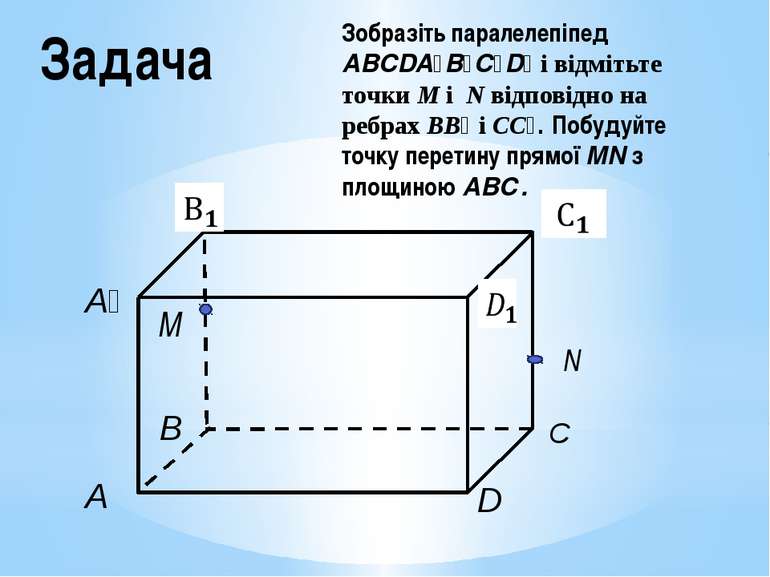
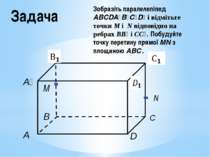
Задача Зобразіть паралелепіпед ABCDA₁B₁C₁D₁ і відмітьте точки M і N відповідно на ребрах ВВ₁ і СС₁. Побудуйте точку перетину прямої MN з площиною АВС. M N С

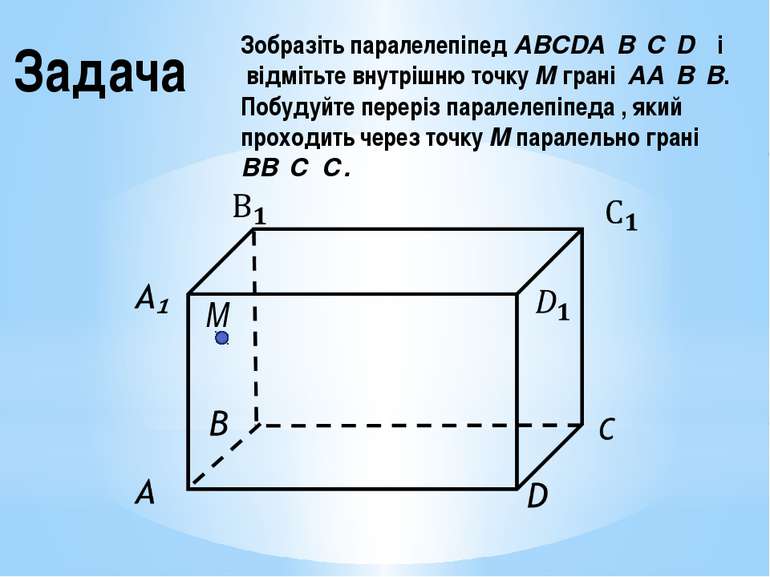
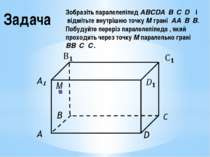
Задача Зобразіть паралелепіпед ABCDA₁B₁C₁D₁ і відмітьте внутрішню точку М грані АА₁В₁В. Побудуйте переріз паралелепіпеда , який проходить через точку М паралельно грані ВВ₁С₁С. M