Презентація на тему:
Ознаки паралельності прямих

Ознаки паралельності прямих Конспект призначений для використання як учителем, так і учнем. Учителю доцільно переглянути презентацію до початку уроку. Учні можуть переглядати презентацію при самостійному вивченні матеріалу. На сторінці конспекту є значок “книги”, при натисканні якого з'являється доведення теореми або розв'язування завдання. Інформація розгортається і згортається одиничним “кліком” на значок “книги” (з'являється “ручка”). Для появи наступного зображення та переходу на інший слайд необхідно “клікати” одноразово мишкою по білому полю. Геометрія – правителька всіх розумових пошуків М.В.Ломоносов Натиснути

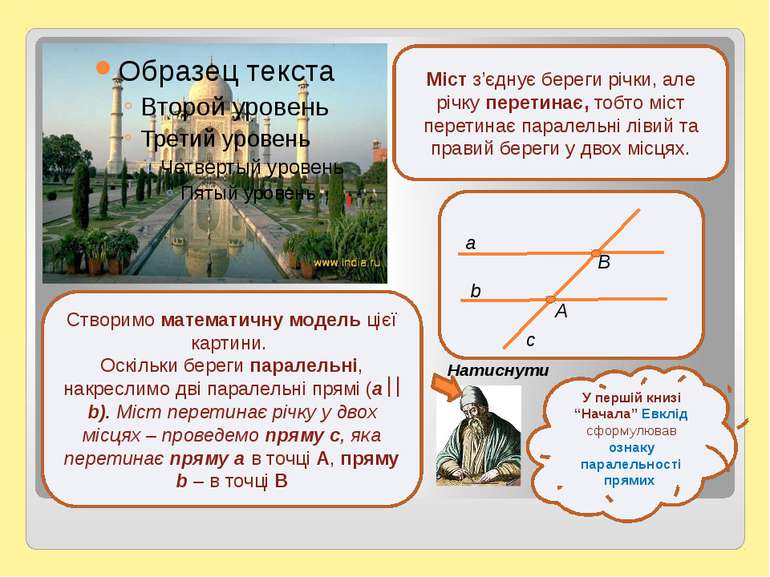
Міст з’єднує береги річки, але річку перетинає, тобто міст перетинає паралельні лівий та правий береги у двох місцях. Створимо математичну модель цієї картини. Оскільки береги паралельні, накреслимо дві паралельні прямі (а b). Міст перетинає річку у двох місцях – проведемо пряму с, яка перетинає пряму а в точці А, пряму b – в точці В У першій книзі “Начала” Евклід сформулював ознаку паралельності прямих a b с А В Натиснути

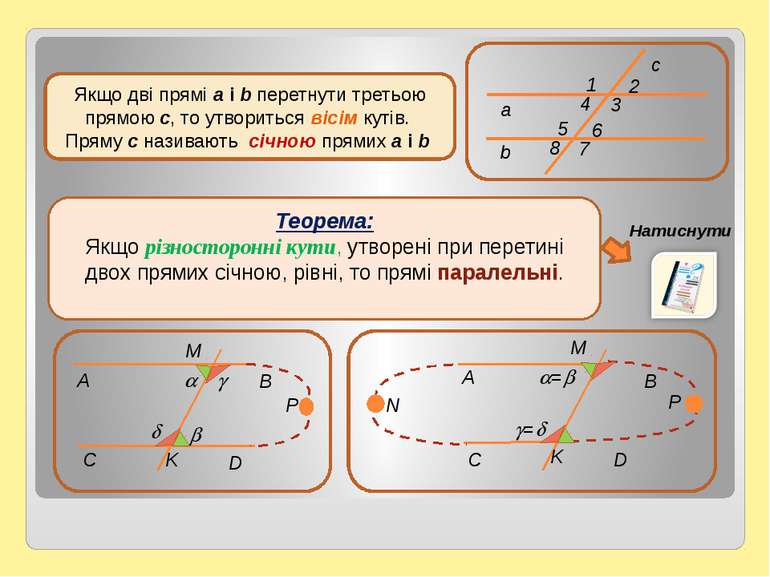
Теорема: Якщо різносторонні кути, утворені при перетині двох прямих січною, рівні, то прямі паралельні. Якщо дві прямі а і b перетнути третьою прямою с, то утвориться вісім кутів. Пряму с називають січною прямих а і b Натиснути А Р M D K А Р M D K = = N c 8 4 7 3 5 6 2 1

Повернутися Доведення: Нехай дано дві прямі АВ, СD і січну МК, = . Треба довести, що АВ СD. Припустимо протилежне: прямі АВ і СD перетинаються у деякій точці Р. Оскільки = , тоді й суміжні їм кути також рівні: = . Розріжемо площину на дві півплощини по прямій МК і накладемо їх одна на одну так, щоб сумістилися кути і та і . Тоді (за аксіомами про відкладання відрізків і кутів) промінь МВ суміститься з променем КС, а КD з МА. 3. За припущенням, промінь МВ перетинався з променем КD у точці Р. Тоді промені КС і МА перетинаються у деякій точці N. 4. Маємо, що через точки Р і N проведено дві різні прямі АВ і СD. Цього бути не може за аксіомою (через дві точки можна провести лише одну пряму). Припущення хибне, і прямі АВ і СD не перетинаються. Теорему доведено.

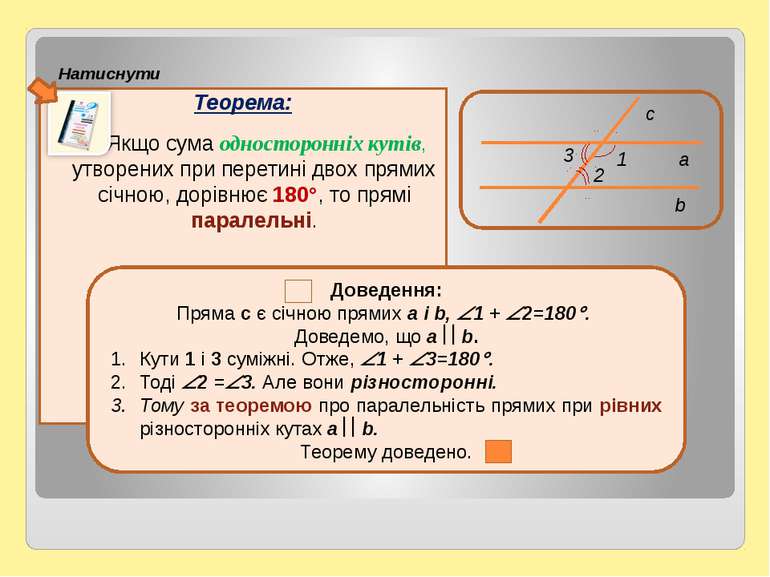
Теорема: Якщо сума односторонніх кутів, утворених при перетині двох прямих січною, дорівнює 180°, то прямі паралельні. Натиснути Доведення: Пряма c є січною прямих а і b, 1 + 2=180 . Доведемо, що а b. Кути 1 і 3 суміжні. Отже, 1 + 3=180 . Тоді 2 = 3. Але вони різносторонні. Тому за теоремою про паралельність прямих при рівних різносторонніх кутах а b. Теорему доведено.

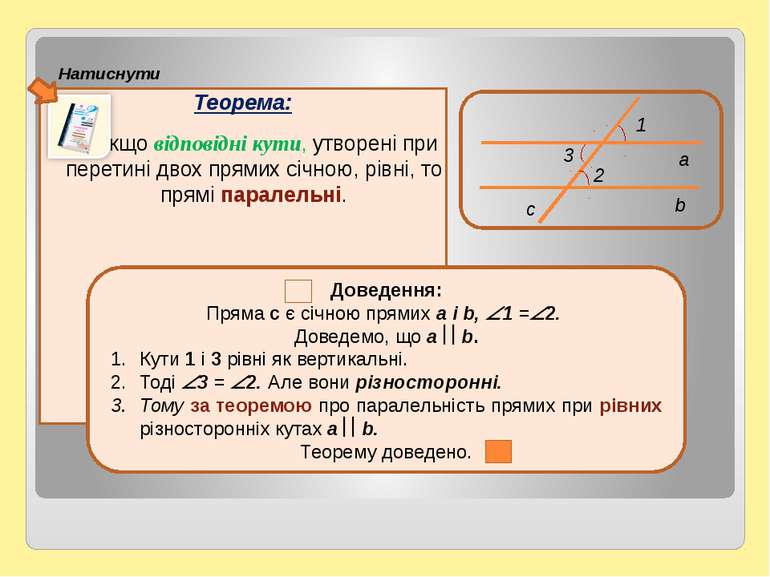
Теорема: Якщо відповідні кути, утворені при перетині двох прямих січною, рівні, то прямі паралельні. Натиснути Доведення: Пряма c є січною прямих а і b, 1 = 2. Доведемо, що а b. Кути 1 і 3 рівні як вертикальні. Тоді 3 = 2. Але вони різносторонні. Тому за теоремою про паралельність прямих при рівних різносторонніх кутах а b. Теорему доведено.

Апостолова Г.В. Геометрія: Підручник для 7-го кл. загальноосвіт. навч. закл. 2-ге вид., доопрац. – К.: Генеза, 2010. – 61 ст. Мерзляк А.Г., Полонський В.Б., Якір М.С. Підручник для 7-го класу. – Х.:Гімназія, 2007. –100-102 ст. Оформила: Олексюк Олена Андріївна, методист НМЦ природничо-математичної освіти ІППО КУ імені Бориса Грінченка