Презентація на тему:
Обчислення площ фігур з допомогою інтеграла

Обчислення площ фігур з допомогою інтеграла Воробйов Леонід Альбертович, учитель математики гімназії № 15 Радянського району, м. Мінськ

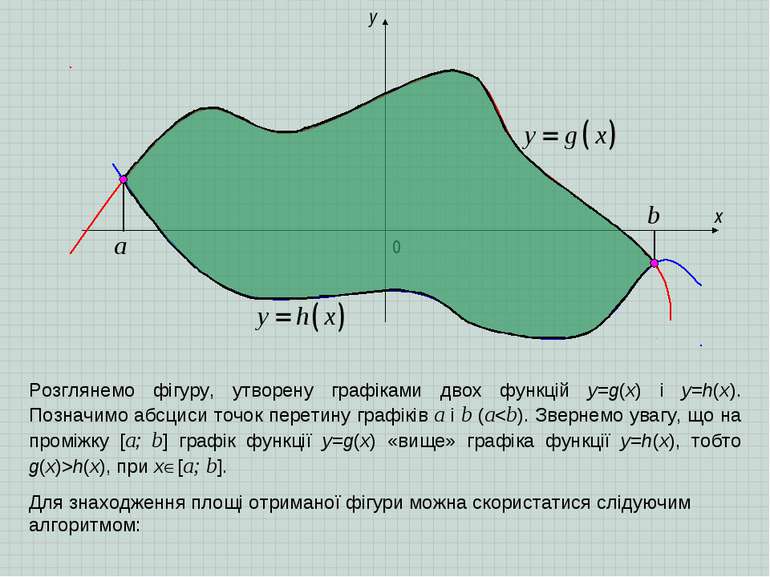
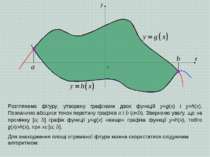
x y 0 a b Розглянемо фігуру, утворену графіками двох функцій y=g(x) і y=h(x). Позначимо абсциси точок перетину графіків a і b (ah(x), при х [а; b]. Для знаходження площі отриманої фігури можна скористатися слідуючим алгоритмом:

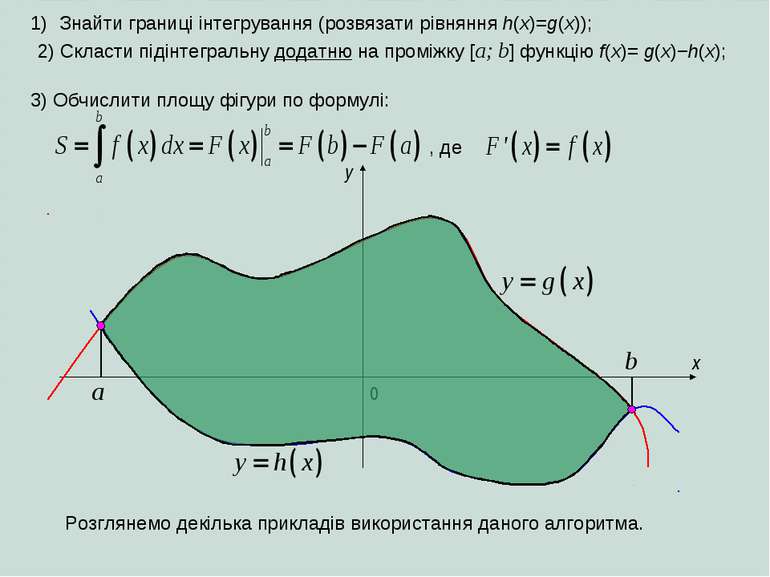
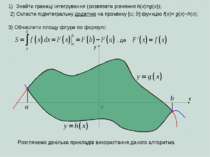
Знайти границі інтегрування (розвязати рівняння h(x)=g(x)); x 0 a b y 2) Скласти підінтегральну додатню на проміжку [a; b] функцію f(x)= g(x)−h(x); 3) Обчислити площу фігури по формулі: , де Розглянемо декілька прикладів використання даного алгоритма.

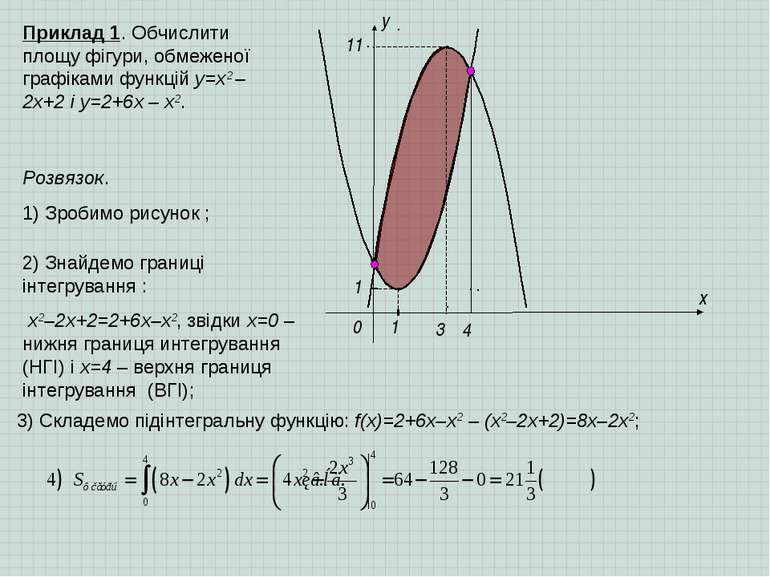
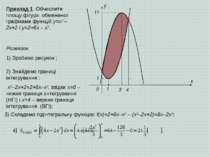
x y 0 1 1 3 11 4 Приклад 1. Обчислити площу фігури, обмеженої графіками функцій y=x2 – 2x+2 і y=2+6x – x2. Розвязок. 1) Зробимо рисунок ; 2) Знайдемо границі інтегрування : x2–2x+2=2+6x–x2, звідки х=0 – нижня границя интегрування (НГІ) і х=4 – верхня границя інтегрування (ВГІ); 3) Складемо підінтегральну функцію: f(x)=2+6x–x2 – (x2–2x+2)=8x–2x2;

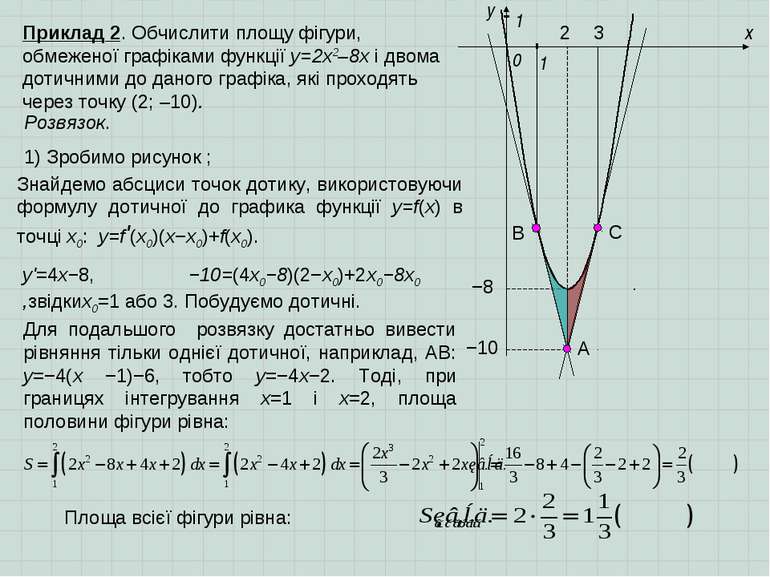
x y 0 Приклад 2. Обчислити площу фігури, обмеженої графіками функції y=2x2–8х і двома дотичними до даного графіка, які проходять через точку (2; –10). 1 1 Розвязок. 1) Зробимо рисунок ; −8 2 −10 Знайдемо абсциси точок дотику, використовуючи формулу дотичної до графика функції y=f(x) в точці х0: y=f'(x0)(x−x0)+f(x0). y'=4x−8, −10=(4x0−8)(2−x0)+2x0−8x0 ,звідких0=1 або 3. Побудуємо дотичні. 3 Для подальшого розвязку достатньо вивести рівняння тільки однієї дотичної, наприклад, АВ: y=−4(х −1)−6, тобто y=−4х−2. Тоді, при границях інтегрування х=1 і х=2, площа половини фігури рівна: А В С Площа всієї фігури рівна:

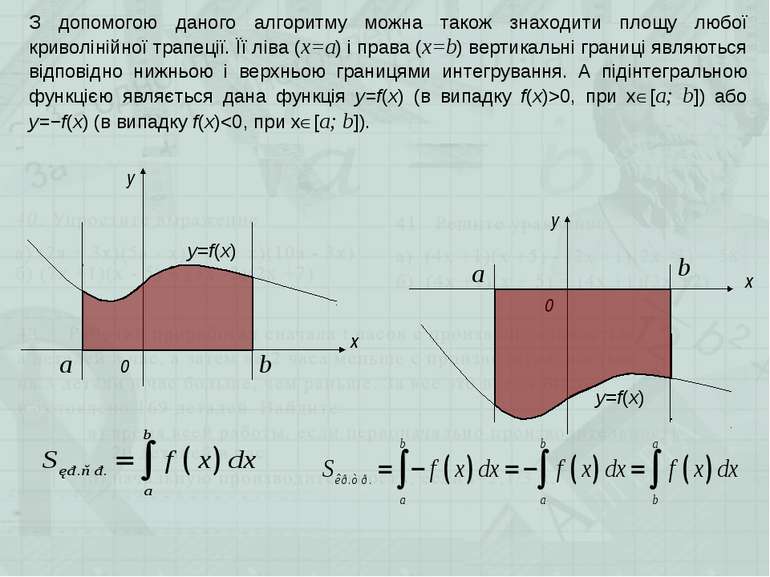
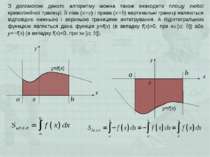
З допомогою даного алгоритму можна також знаходити площу любої криволінійної трапеції. Її ліва (х=а) і права (х=b) вертикальні границі являються відповідно нижньою і верхньою границями интегрування. А підінтегральною функцією являється дана функція y=f(x) (в випадку f(x)>0, при х [a; b]) або y=−f(x) (в випадку f(x)