Презентація на тему:
Коло

коло це множина всіх точок площини, рівновіддалених від фіксованої точки. Ця точка є центром кола , а відстань – радіусом кола. (АО=СО=ВО=DO=SO=FO) -

1.Засвоїти поняття: чотирикутник, вписаний в коло; чотирикутник, описаний навколо кола; розглянути теореми про вписані і опасанні чотирикутники, та схеми їх доведення. 2. Формувати і розвивати вміння використовувати геометричні поняття під час розв'язування задач, робити висновки, вести евристичну бесіду, логічне та абстрактне мислення, математичне мовлення , навички організаційної роботи на уроці 3. Виховувати уважність, свідоме ставлення до навчання, вміння організовувати свою роботу на уроці, самооцінку та самоконтроль

Який з чотирикутників вписаний? Пояснити.

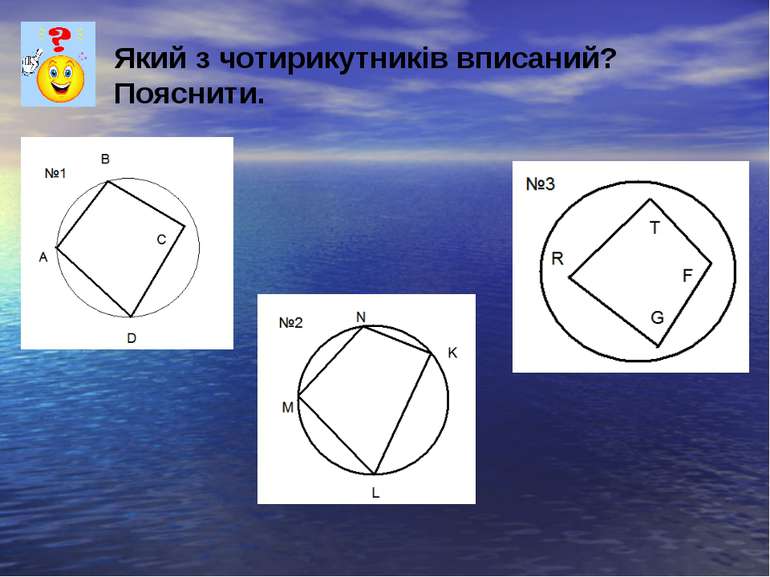
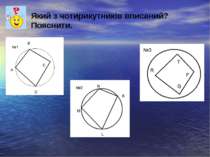
Чотирикутник, всі вершини якого лежать на колі, називається вписаним у це коло, а коло описаним навколо даного чотирикутника.

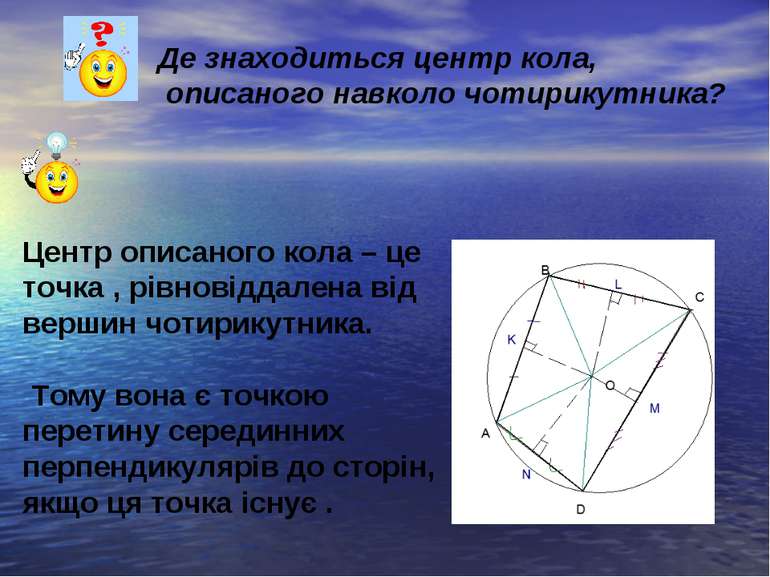
Де знаходиться центр кола, описаного навколо чотирикутника? Центр описаного кола – це точка , рівновіддалена від вершин чотирикутника. Тому вона є точкою перетину серединних перпендикулярів до сторін, якщо ця точка існує .

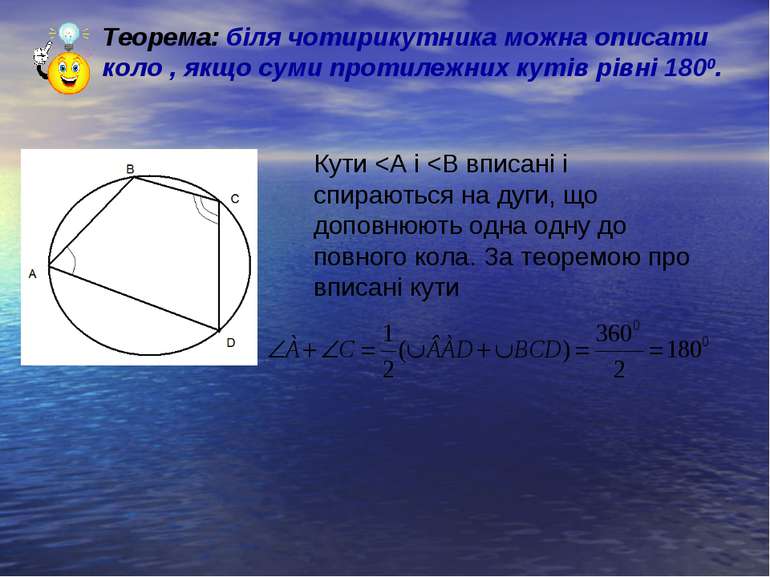
Теорема: біля чотирикутника можна описати коло , якщо суми протилежних кутів рівні 1800. Кути

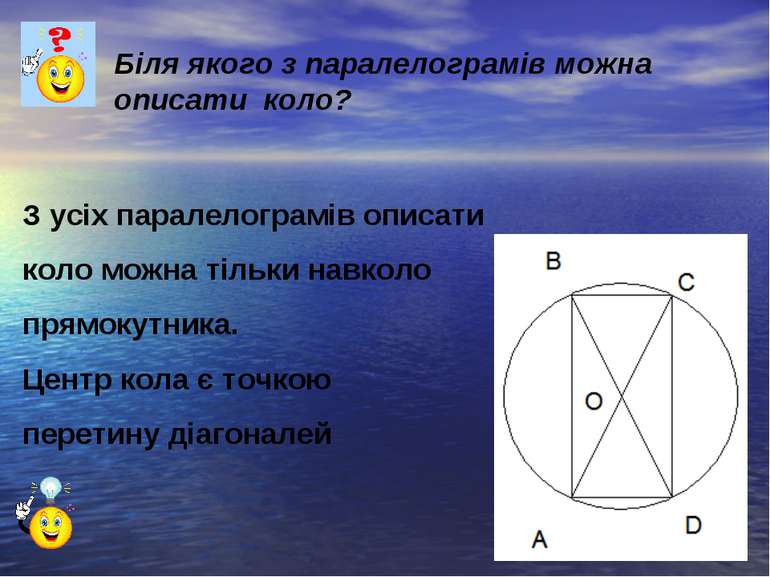
Біля якого з паралелограмів можна описати коло? З усіх паралелограмів описати коло можна тільки навколо прямокутника. Центр кола є точкою перетину діагоналей

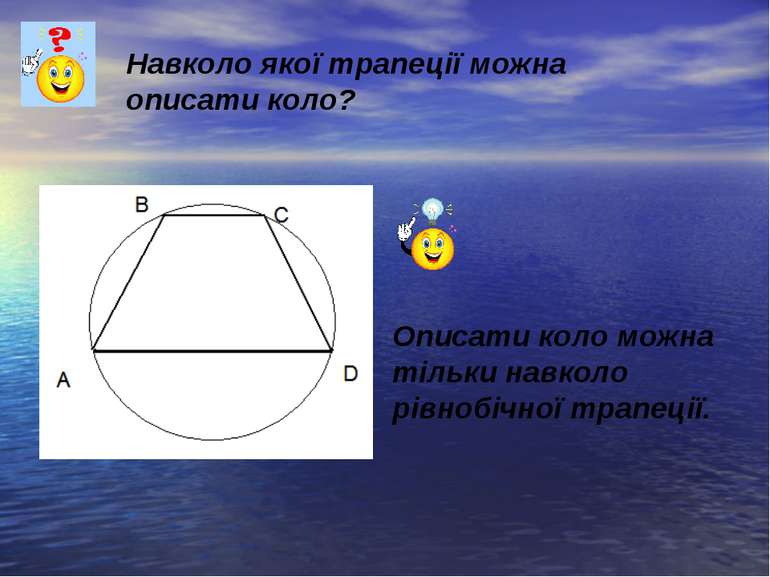
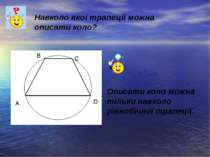
Навколо якої трапеції можна описати коло? Описати коло можна тільки навколо рівнобічної трапеції.

На якому з малюнків зображений описаний чотирикутник?

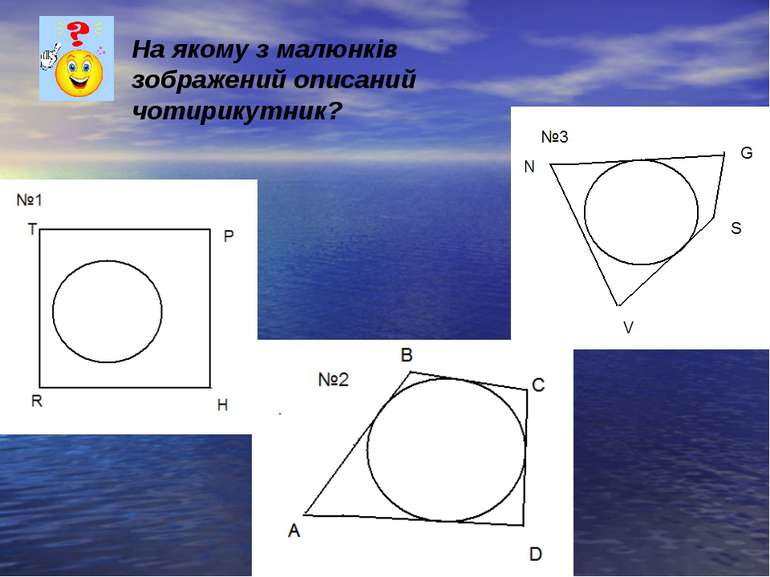
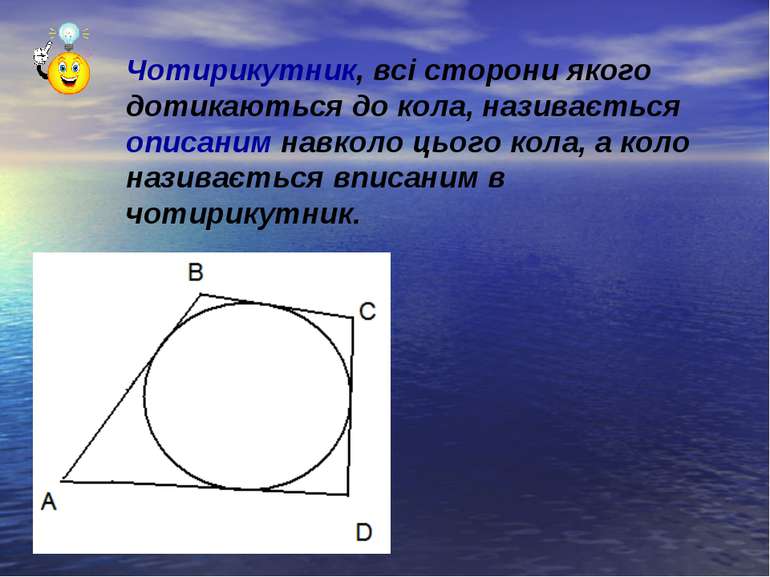
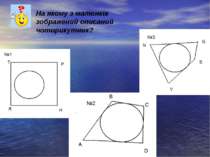
Чотирикутник, всі сторони якого дотикаються до кола, називається описаним навколо цього кола, а коло називається вписаним в чотирикутник.

Де знаходиться центр кола, вписаного в чотирикутник? Центр кола , вписаного в чотирикутник , це точка рівновіддалена від сторін чотирикутника. Тому вона є точкою перетину бісектрис внутрішніх кутів чотирикутника . ( якщо для многокутника ця точка існує ).

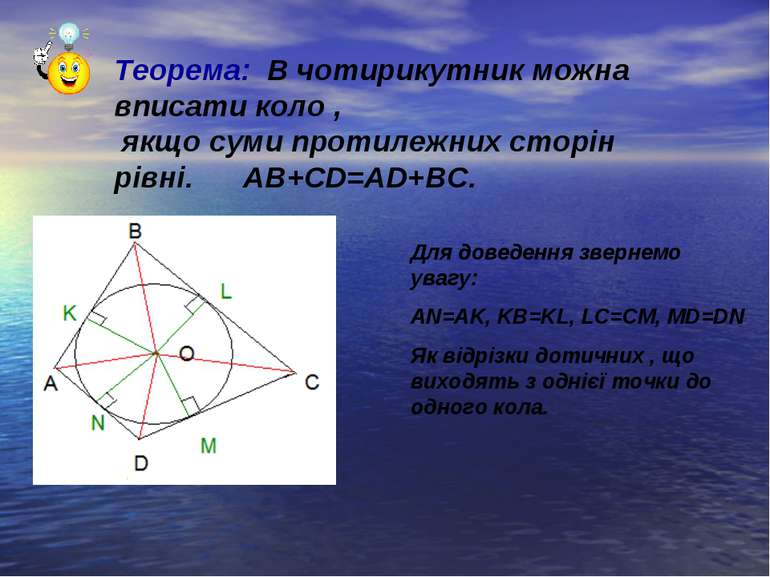
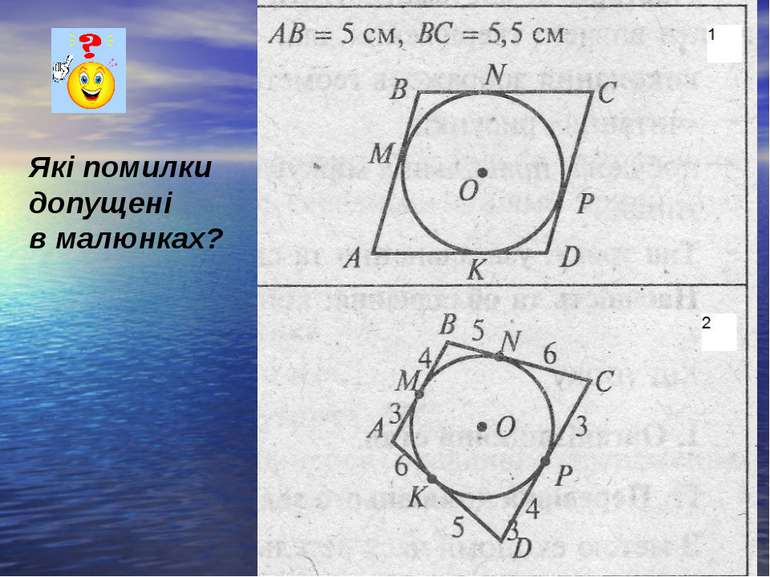
Теорема: В чотирикутник можна вписати коло , якщо суми протилежних сторін рівні. АВ+СD=AD+ВС. Для доведення звернемо увагу: AN=AK, KB=KL, LC=CM, MD=DN Як відрізки дотичних , що виходять з однієї точки до одного кола.

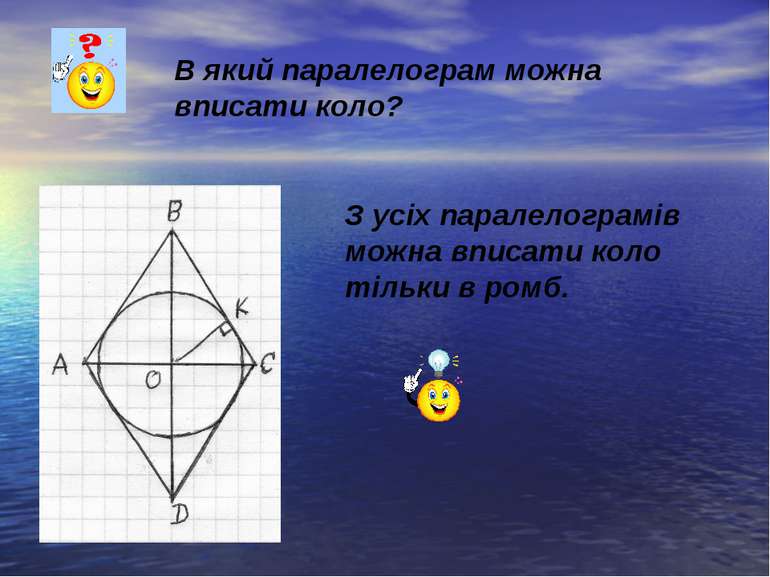
В який паралелограм можна вписати коло? З усіх паралелограмів можна вписати коло тільки в ромб.

В яку трапецію можна вписати коло? Якщо в трапецію вписане коло то : суми бічних сторін дорівнюють сумі основ; висота дорівнює двом радіусам вписаного кола ; бічну сторону видно з центра вписаного кола під прямим кутом

Які помилки допущені в малюнках?

Які помилки допущені в малюнках?

Чотирикутник вписаний в коло. Знайти невідомі кути, якщо: Два кути 460 і 1250. У трапеції один з кутів 800.

Знайти периметр чотирикутника, якщо в нього можна вписати коло: Три послідовні сторони 7см, 9см та 8см. У трапеції бічні сторони 3см і 11см.

В трапеції три сторони рівні, і дорівнюють d, а діагональ перпендикулярна до бічної сторони. Знайдіть радіус описаного кола та кути трапеції.

Розв`язування задачі: 1.

підручник ст. 69-72. № 389,390,395 №417*