Презентація на тему:
Геометричні перетворення

Геометричні перетворення Геометрія є прообразом краси світу (Й.Кеплер)

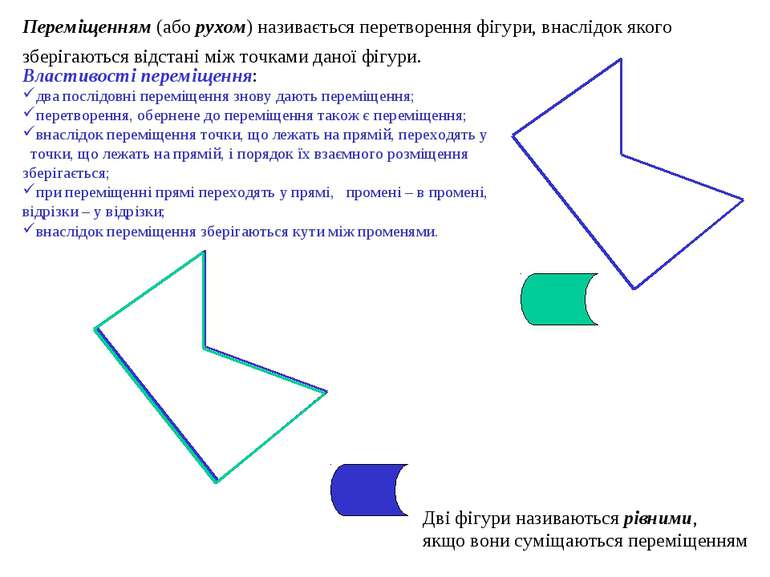
Переміщенням (або рухом) називається перетворення фігури, внаслідок якого зберігаються відстані між точками даної фігури. Дві фігури називаються рівними, якщо вони суміщаються переміщенням Властивості переміщення: два послідовні переміщення знову дають переміщення; перетворення, обернене до переміщення також є переміщення; внаслідок переміщення точки, що лежать на прямій, переходять у точки, що лежать на прямій, і порядок їх взаємного розміщення зберігається; при переміщенні прямі переходять у прямі, промені – в промені, відрізки – у відрізки; внаслідок переміщення зберігаються кути між променями.

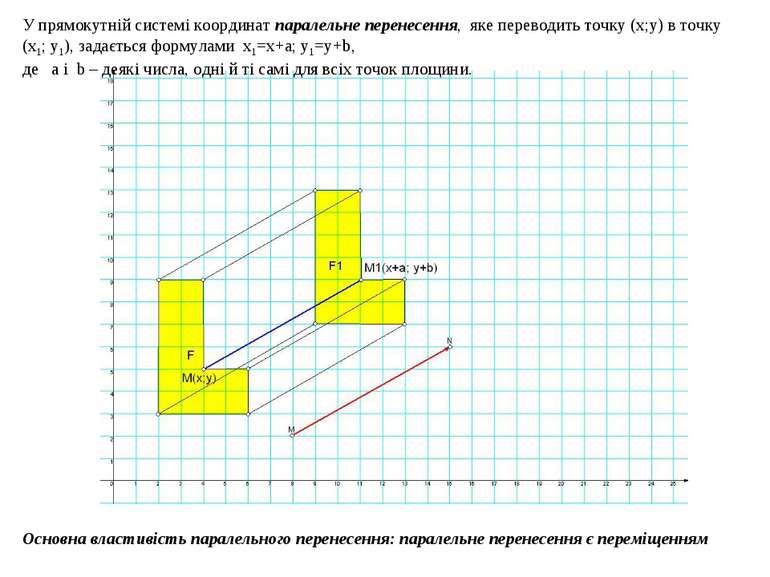
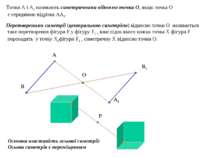
Паралельним перенесенням фігури F у напрямі променя ОА на відстань а називається таке перетворення фігури F у фігуру F/ , внаслідок якого кожна точка Х фігури F переходить у точку Х/ фігури F/ так, що промені ХХ/ і ОА співнапрямлені і ХХ/ =а О А Х Х/ Основна властивість паралельного перенесення: паралельне перенесення є переміщенням У прямокутній системі координат паралельне перенесення, яке переводить точку (х;у) в точку (х1; у1), задається формулами х1=х+а; у1=у+b, де a і b – деякі числа, одні й ті самі для всіх точок площини.

Основна властивість паралельного перенесення: паралельне перенесення є переміщенням У прямокутній системі координат паралельне перенесення, яке переводить точку (х;у) в точку (х1; у1), задається формулами х1=х+а; у1=у+b, де a і b – деякі числа, одні й ті самі для всіх точок площини.

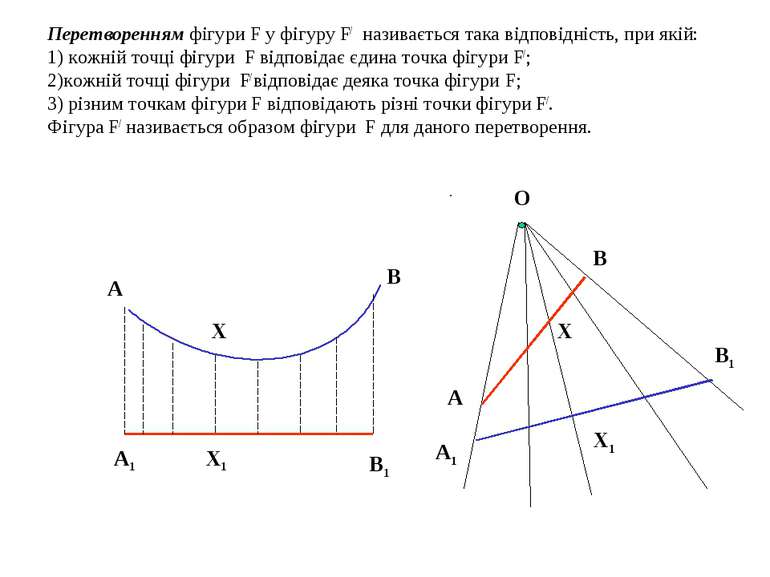
Перетворенням фігури F у фігуру F/ називається така відповідність, при якій: 1) кожній точці фігури F відповідає єдина точка фігури F/; 2)кожній точці фігури F/ відповідає деяка точка фігури F; 3) різним точкам фігури F відповідають різні точки фігури F/. Фігура F/ називається образом фігури F для даного перетворення. А А1 В Х Х1 В1 О А В А1 В1 Х Х1

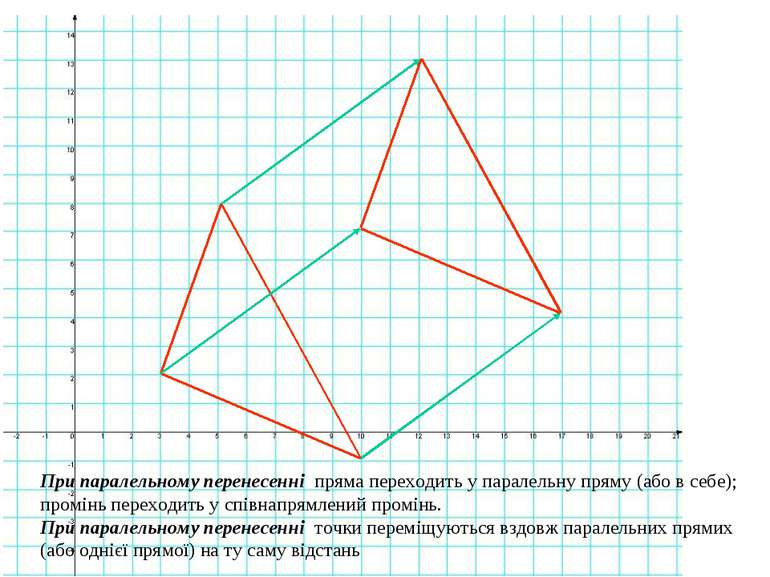
При паралельному перенесенні пряма переходить у паралельну пряму (або в себе); промінь переходить у співнапрямлений промінь. При паралельному перенесенні точки переміщуються вздовж паралельних прямих (або однієї прямої) на ту саму відстань

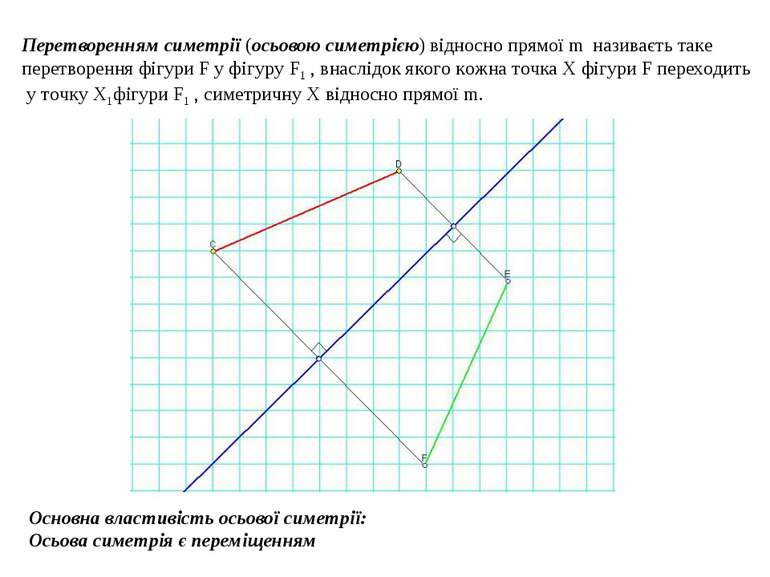
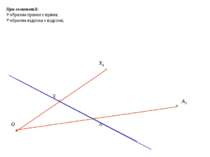
Перетворенням симетрії (осьовою симетрією) відносно прямої m називаєть таке перетворення фігури F у фігуру F1 , внаслідок якого кожна точка Х фігури F переходить у точку Х1фігури F1 , симетричну Х відносно прямої m. Основна властивість осьової симетрії: Осьова симетрія є переміщенням

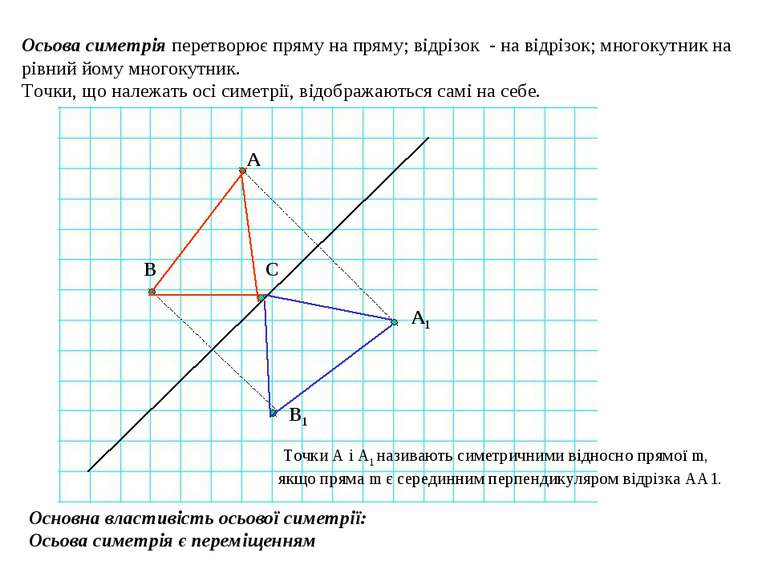
Осьова симетрія перетворює пряму на пряму; відрізок - на відрізок; многокутник на рівний йому многокутник. Точки, що належать осі симетрії, відображаються самі на себе. А1 А В В1 Основна властивість осьової симетрії: Осьова симетрія є переміщенням С Точки А і А1 називають симетричними відносно прямої m, якщо пряма m є серединним перпендикуляром відрізка АА1.

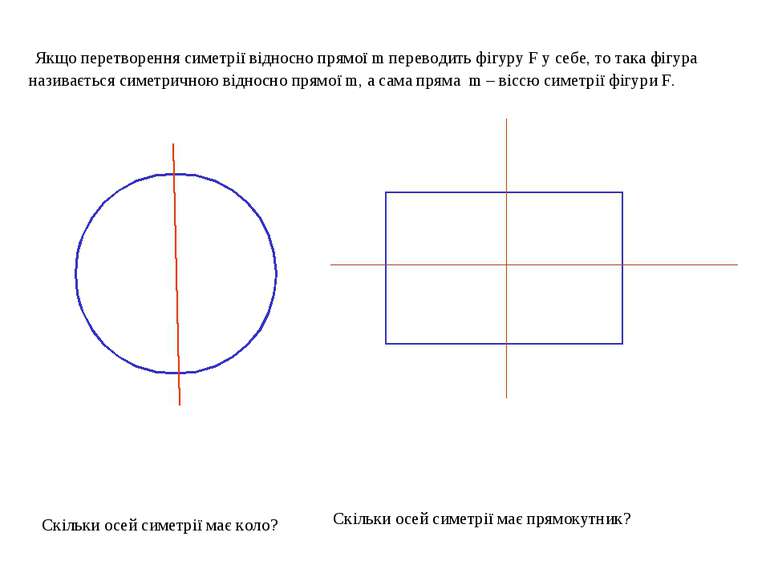
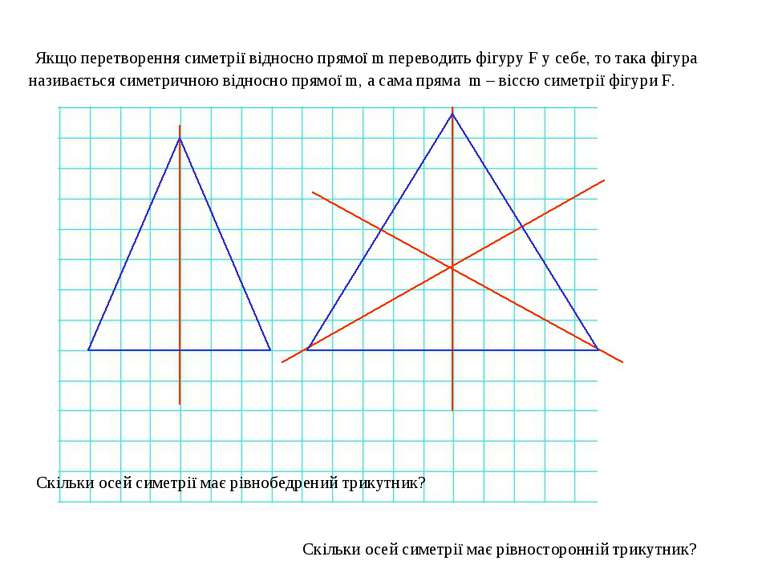
Якщо перетворення симетрії відносно прямої m переводить фігуру F у себе, то така фігура називається симетричною відносно прямої m, а сама пряма m – віссю симетрії фігури F. Скільки осей симетрії має коло? Скільки осей симетрії має прямокутник?

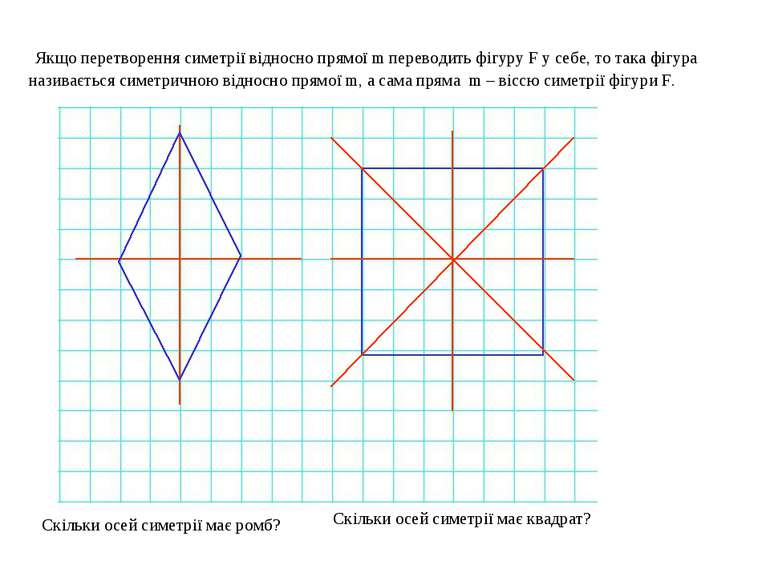
Якщо перетворення симетрії відносно прямої m переводить фігуру F у себе, то така фігура називається симетричною відносно прямої m, а сама пряма m – віссю симетрії фігури F. Скільки осей симетрії має ромб? Скільки осей симетрії має квадрат?

Якщо перетворення симетрії відносно прямої m переводить фігуру F у себе, то така фігура називається симетричною відносно прямої m, а сама пряма m – віссю симетрії фігури F. Скільки осей симетрії має рівнобедрений трикутник? Скільки осей симетрії має рівносторонній трикутник?

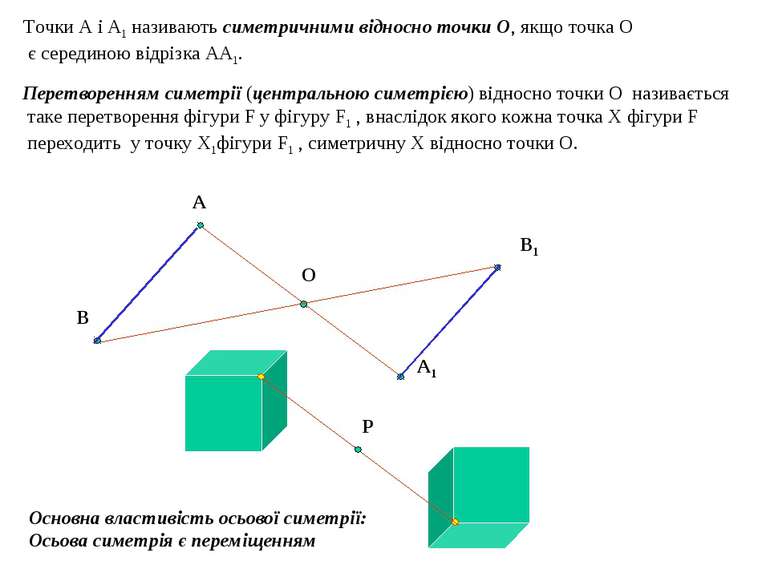
Точки А і А1 називають симетричними відносно точки О, якщо точка О є серединою відрізка АА1. Основна властивість осьової симетрії: Осьова симетрія є переміщенням А А1 O Перетворенням симетрії (центральною симетрією) відносно точки О називається таке перетворення фігури F у фігуру F1 , внаслідок якого кожна точка Х фігури F переходить у точку Х1фігури F1 , симетричну Х відносно точки О. В В1 Р

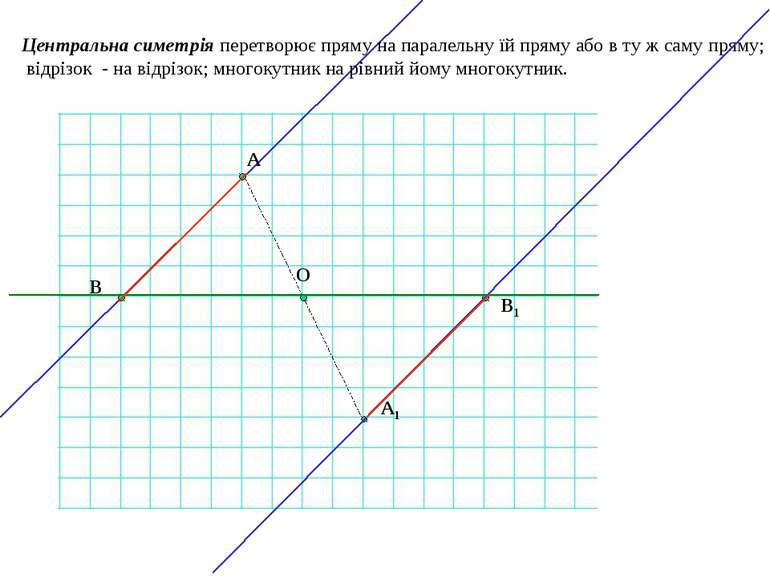
Центральна симетрія перетворює пряму на паралельну їй пряму або в ту ж саму пряму; відрізок - на відрізок; многокутник на рівний йому многокутник. А1 А В В1 О

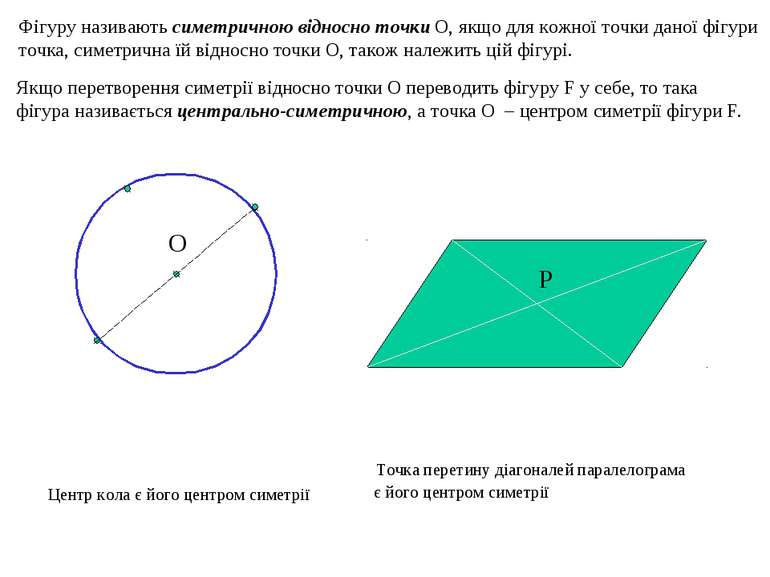
Фігуру називають симетричною відносно точки О, якщо для кожної точки даної фігури точка, симетрична їй відносно точки О, також належить цій фігурі. Якщо перетворення симетрії відносно точки О переводить фігуру F у себе, то така фігура називається центрально-симетричною, а точка О – центром симетрії фігури F. Центр кола є його центром симетрії Р Точка перетину діагоналей паралелограма є його центром симетрії О

Поворотом фігури F навколо точки О на кут називається перетворення фігури F у фігуру F1 , внаслідок якого кожна точка Х фігури F переходить у точку Х1фігури F1 так, що ОХ1 =ОХ і ХОХ1 = . Точку О називають центром повороту, а кут – кутом повороту. Основна властивість повороту: поворот є переміщенням. Тобто якщо фігура F1 – образ фігури F при повороті, то F = F1 O F F1 X X1 a

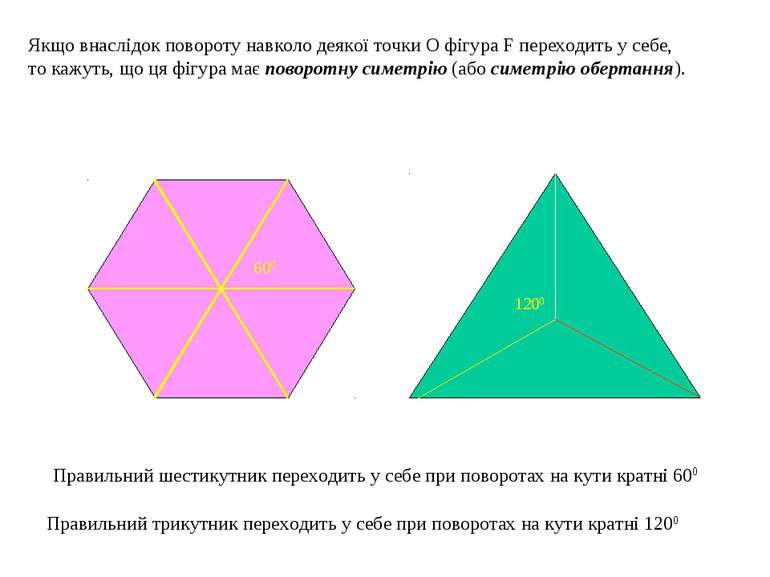
Якщо внаслідок повороту навколо деякої точки О фігура F переходить у себе, то кажуть, що ця фігура має поворотну симетрію (або симетрію обертання). Правильний шестикутник переходить у себе при поворотах на кути кратні 600 Правильний трикутник переходить у себе при поворотах на кути кратні 1200 600 1200

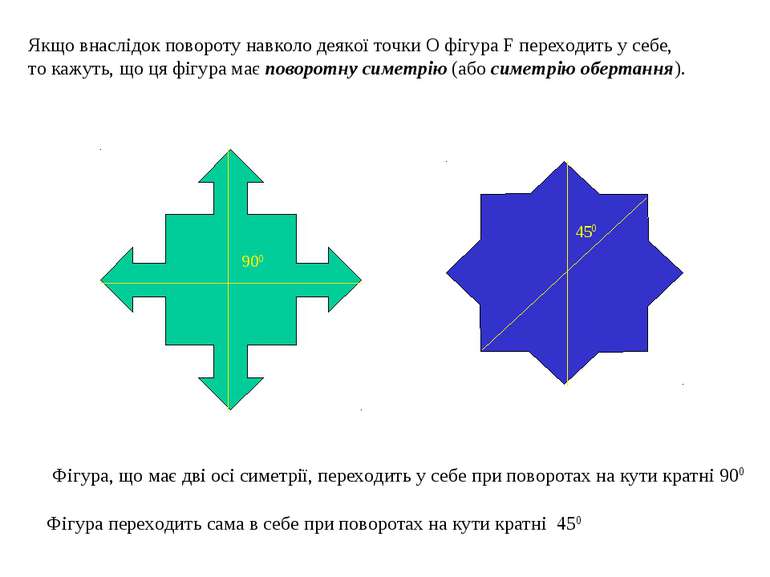
Якщо внаслідок повороту навколо деякої точки О фігура F переходить у себе, то кажуть, що ця фігура має поворотну симетрію (або симетрію обертання). Фігура, що має дві осі симетрії, переходить у себе при поворотах на кути кратні 900 Фігура переходить сама в себе при поворотах на кути кратні 450 450 900

Перетворенням подібності (подібністю) називається таке перетворення фігури F у фігуру F1 , внаслідок якого відстані між точками змінюються в тому самому відношенні k (k>0). Число k>0 називають коефіцієнтом подібності. Дві фігури називаються подібними, якщо вони переводяться одна в одну перетворенням подібності.

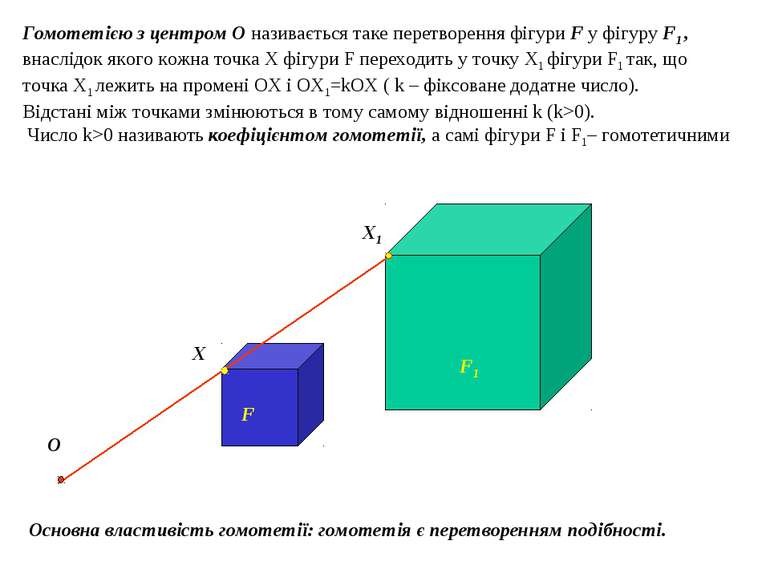
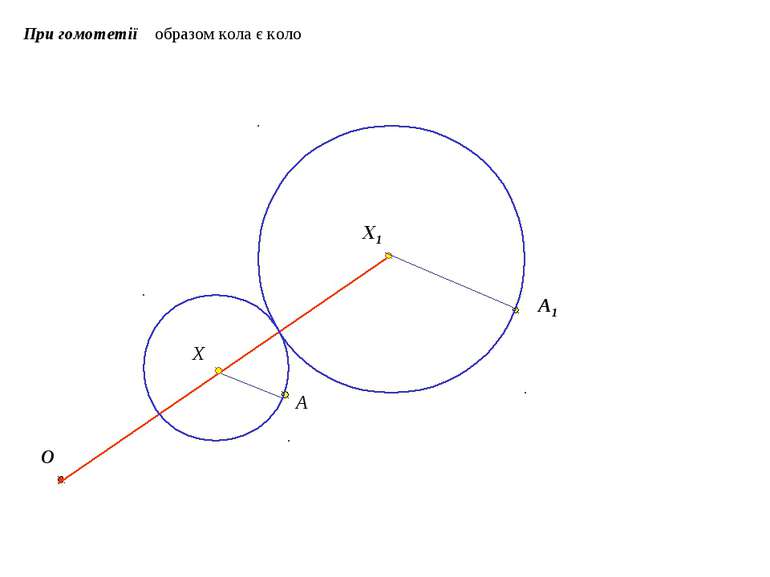
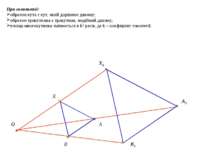
Гомотетією з центром О називається таке перетворення фігури F у фігуру F1 , внаслідок якого кожна точка Х фігури F переходить у точку Х1 фігури F1 так, що точка Х1 лежить на промені ОХ і OX1=kOX ( k – фіксоване додатне число). Відстані між точками змінюються в тому самому відношенні k (k>0). Число k>0 називають коефіцієнтом гомотетії, а самі фігури F і F1– гомотетичними O Х Х1 F F1 Основна властивість гомотетії: гомотетія є перетворенням подібності.

При гомотетії: образом прямої є пряма; образом відрізка є відрізок; O Х Х1 A A1

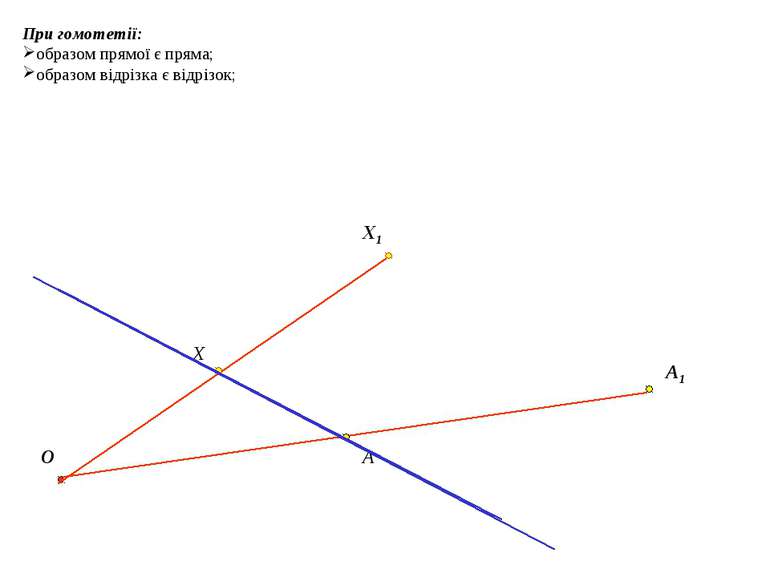
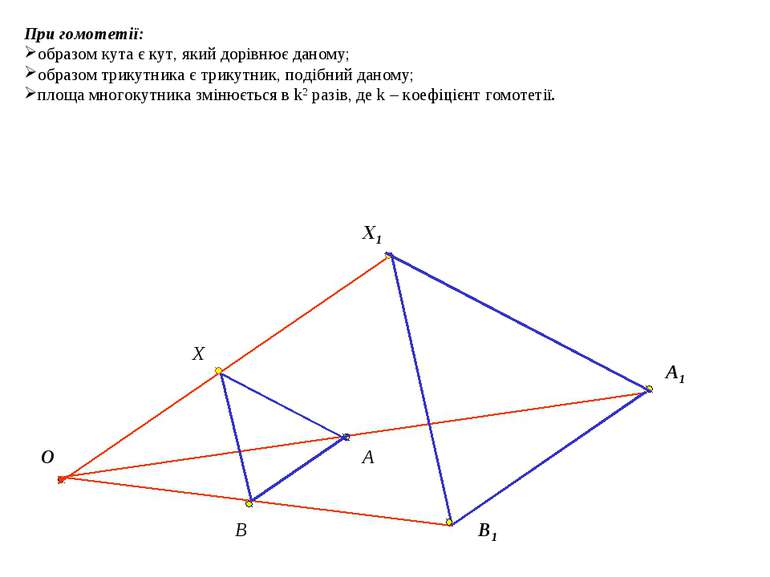
При гомотетії: образом кута є кут, який дорівнює даному; образом трикутника є трикутник, подібний даному; площа многокутника змінюється в k2 разів, де k – коефіцієнт гомотетії. O Х Х1 A A1 B B1

При гомотетії образом кола є коло O Х Х1 A A1

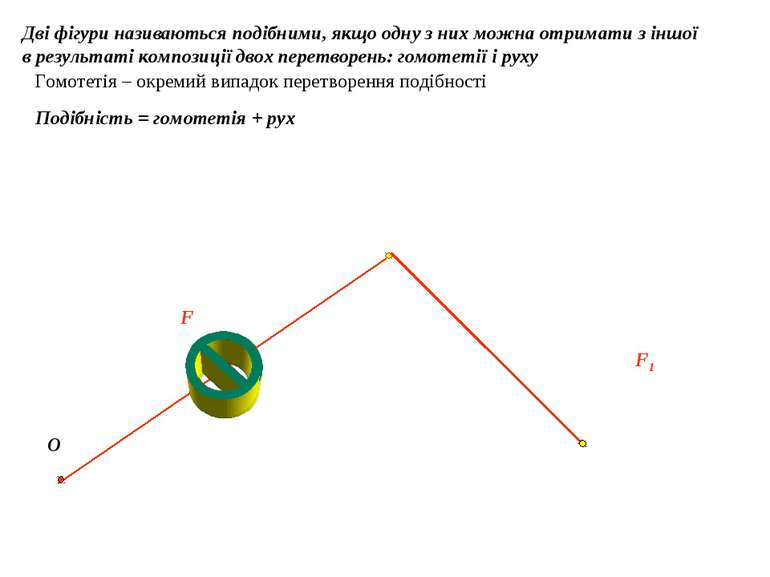
Дві фігури називаються подібними, якщо одну з них можна отримати з іншої в результаті композиції двох перетворень: гомотетії і руху O F F1 Подібність = гомотетія + рух Гомотетія – окремий випадок перетворення подібності