Презентація на тему:
Чотирикутники

Девіз уроку: Мало мати хороший розум, головне – добре його застосовувати Рене Декарт

Повторення теоретичного матеріалу Чотирикутник, у якого кожні дві протилежні сторони паралельні називають ….. У паралелограма протилежні сторони…. У паралелограма протилежні кути …. Перпендикуляр опущений з будь-якої точки прямої, яка містить сторону паралелограма, на пряму, що містить протилежну сторону, називається…. Сума будь-яких двох сусідніх кутів паралелограма дорівнює… Якщо в чотирикутнику діагоналі точкою перетину діляться пополам, то цей чотирикутник називається…. Прямокутником називається паралелограм, у якого …. В прямокутника діагоналі …. Якщо один з кутів паралелограма прямий, то цей паралелограм називається…. Паралелограм у якого всі сторони рівні називається…. Діагоналі ромба…. Прямокутник у якого всі сторони рівні називається …. Паралелограм у якого діагональ є бісектрисою його кута називають…. Діагоналі в квадрата …. Закінчити речення: бліц опитування

Задачі за готовими малюнками 1 2 3

1. Знайти: Дано:

2. Дано: Найти:

3. Дано: Знайти:

Тема уроку: Трапеція. Види та властивості трапецій. Середня лінія.

* * Мета уроку: Формувати поняття про трапецію та її властивості; Формувати знання про середню лінію трапеції; Навчити застосовувати набуті знання та вміння до розв’язування задач

– маємо формувати поняття про трапецію її види. Вивчити теорему про середню лінію трикутника – ефективно використовувати урок – творчо підходити до роботи – активно співпрацювати

Вивчення нового матеріалу Трапеція та її елементи Види трапецій та їх властивості Середня лінія трапеції План вивчення:

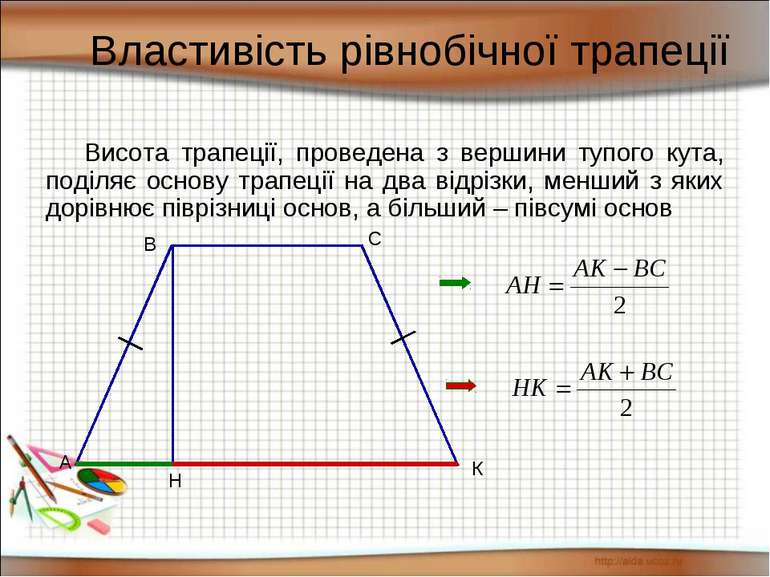
Властивість рівнобічної трапеції Висота трапеції, проведена з вершини тупого кута, поділяє основу трапеції на два відрізки, менший з яких дорівнює піврізниці основ, а більший – півсумі основ А В С К Н

Розв’язання задач У рівнобічній трапеції один з кутів дорівнює 600, бічна сторона дорівнює 24 см, а сума основ дорівнює 44 см. Знайти основи трапеції. Задача 1:

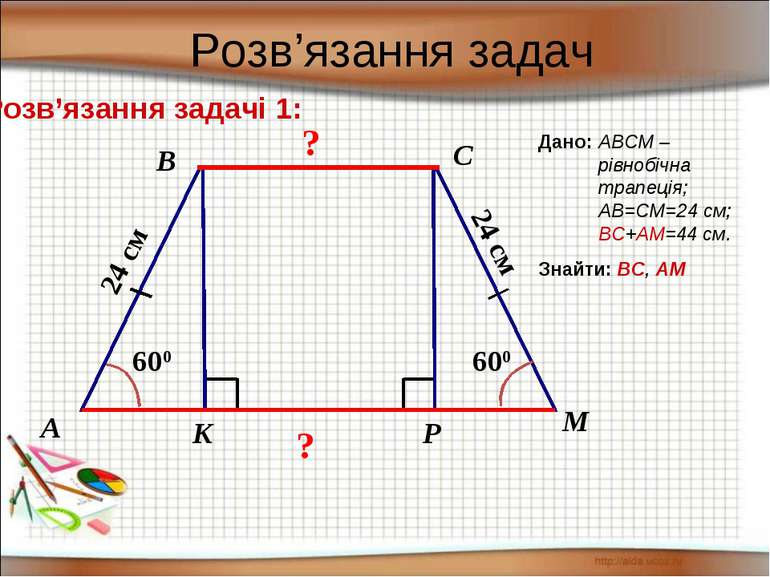
Розв’язання задач Розв’язання задачі 1: ? ? K 600 M P 600 24 см А В С Дано: ABCM – рівнобічна трапеція; АВ=СМ=24 см; ВС+АМ=44 см. Знайти: ВС, АМ 24 см

Розв’язання задач Середня лінія прямокутної трапеції дорівнює 12 см, а висота, проведена з вершини тупого кута трапеції, поділяє її основу на відрізки, довжини яких відносяться як 3 : 2, рахуючи від вершини прямого кута. Знайдіть основи трапеції. Задача 2:

Розв’язання задач Розв’язання задачі 2: D А С Дано: ABCD – прямокутна трапеція; DH : AH=3 : 2 BH – висота; MN=12 см – середня лінія. Знайти: ВС, АD В Н M N 2k 3k ? ?

Робота в групах У рівнобічній трапеції діагональ поділяє гострий кут навпіл, а її основи відносяться як 3 : 5. Знайдіть середню лінію трапеції, якщо її периметр дорівнює 168 см. Задача 3:

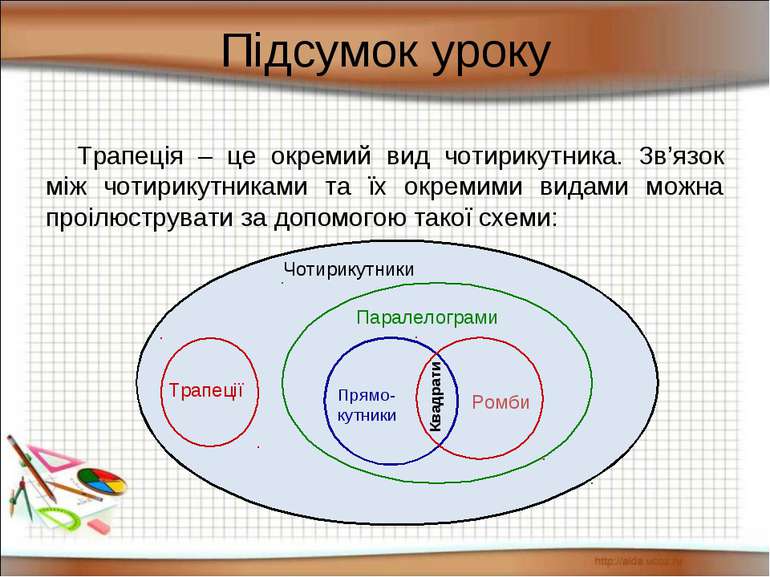
Підсумок уроку Трапеція – це окремий вид чотирикутника. Зв’язок між чотирикутниками та їх окремими видами можна проілюструвати за допомогою такої схеми: Чотирикутники Трапеції Паралелограми Прямо-кутники Ромби Квадрати

Домашнє завдання Вивчити п. 10 (стор.57). Геометрія 8, для класів з поглибленим вивченням Вивчити §5. Геометрія 8, для загальноосвітніх шкіл Виконати впр. 213, 222(б), 232

Трапеція та її елементи

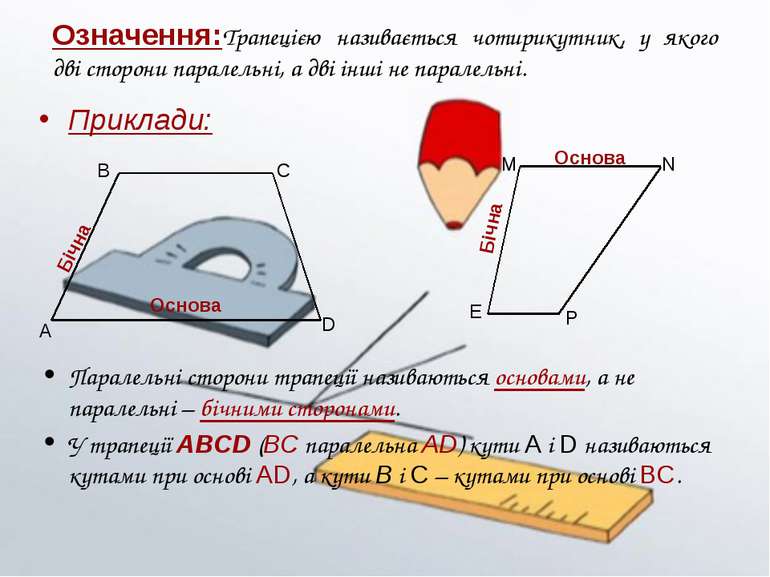
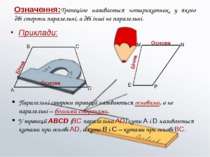
Означення:Трапецією називається чотирикутник, у якого дві сторони паралельні, а дві інші не паралельні. Приклади: Паралельні сторони трапеції називаються основами, а не паралельні – бічними сторонами. У трапеції ABCD (BC паралельна AD) кути A і D називаються кутами при основі AD, а кути B і C – кутами при основі BC.

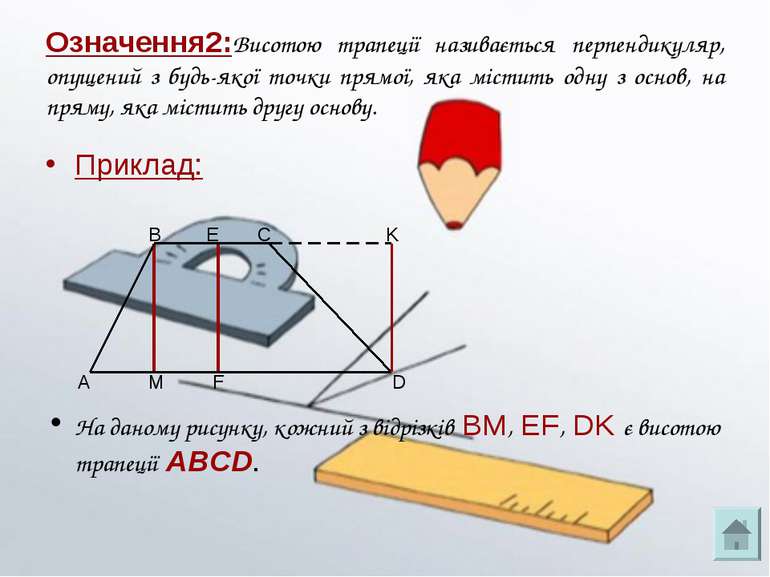
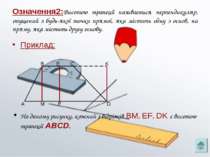
Означення2:Висотою трапеції називається перпендикуляр, опущений з будь-якої точки прямої, яка містить одну з основ, на пряму, яка містить другу основу. Приклад: На даному рисунку, кожний з відрізків BM, EF, DK є висотою трапеції ABCD.