Презентація на тему:
Механічні властивості біологічних тканин

до книжки: “Медична і біологічна фізика” під редакцією члена-кореспондента АПН України професора О. В. Чалого, том I , за темою: “Біомеханіка, Біореологія та Гемодинаміка”, сторінки 170-258 Презентація

Роботу виконав: Учень 11-б класу, III групи УМЛ НМУ ім. О. О. Богомольця Медведєв Богдан Вчитель: Лялько Віра Іванівна

Механічні властивості біологічних тканин (ст. 170-182)

Зміст Поняття біомеханіки, біореології та гемодинаміки Механічні властивості біологічних тканин Деформація біологічних тканин Об'ємна деформація Деформація кручення Деформація сталі Деформація біологічних тканин Кісткова тканина Колагенові волокна Еластинові волокна Діаграма розтягу судин Висновок

Розглянемо найважливіші механічні властивості біологічних тканин, завдяки яким здійснюються різноманітні механічні явища- такі, як функціонування опорно-рухового апарата, процеси деформацій тканин і клітин, розповсюдження хвиль пружної деформації, скорочення і розслаблення м’язів, рух рідких і газоподібних біологічних середовищ. Серед цих властивостей виділяють: -пружність – здатність тіл відновлювати розміри (форму чи об’єм) після зняття навантажень; - жорсткість- здатність матеріалу протидіяти зовнішнім навантаженням; - еластичність- здатність матеріалу змінювати розміри під дією зовнішніх навантажень; Зміст

- міцність- здатність тіл протидіяти руйнуванню під дією зовнішніх сил; - пластичність- здатність тіл зберігати(повністтю або частково)зміну розмірів після зняття навантажень; - крихкість- здатність матеріалу руйнуватися без утворення помітних залишкових деформацій; - в’язкість- динамічна властивість, яка храктеризує властивість тіла протидіяти зміні його форми при дії тангенціальних напружень.; - плинність- динамічна властивість середовища, яка характеризує здатніть окремих його шарів перемішуватись, з деякою швидкісттю у просторі відносно інших шарів цього середовища. Зміст

Деформації Усі реальні тіла здатні деформуватись.Зміну форми чи об’єму тіла під дією зовнішніх сил називають деформацією.Розрізняють пружні та пластичні деформації.Пружніми називають деформації, якіповністтю зникають після припинення дії зовнішніх сил.При пластичних деформаціях тіло залишається у деформованому стані після припинення дії зовнішніх сил. Відношення абсолютної деформації ∆X до первісного знчення X зветься відносною деформацією. ε=∆X/X0 Зовнішня сила, яка діє на ділянку тіла врівноважується силою пружності, що діє на дану ділянку з боку сусідньоїФізична величина, яка дорівнює пружній силі, що припадає на одиницю площі перерізу тіла, зветься напруженням. σ = d * Fпр/dS Напруження в пружно деформованому тілі прямо пропорційне до його відносної деформації. σ =E * ε де E – модуль пружності, його величина визначається властивостями матеріалу, з якого виготовлене тіло. Зміст

Об’ємна деформація Об’мна деіормація виникає при рівномірному розподілі стискуючих або розтягуючих сил по поверхні тіла. Закон Гука у цьому випадку матиме вигляд σ =X*∆V/V0 де X- модуль об’мної пружності, а ∆V та V0 – зміна об’єму тіла та первісний об’єим відповідно. Зміст

Деформація кручення Деформація крученя виникає у зразку, коли один його переріз нерухомий, а в іншому діє пара сил, момент якої спрямований вздовж осі зразка При деформаціях тіл часто виявляються в’язко-пружні властивості, які полягають у тому , що напруження залежить не лише від деформації(ε), а й від швидкості її зміни з часом., тобто похідної ε’. Зміст

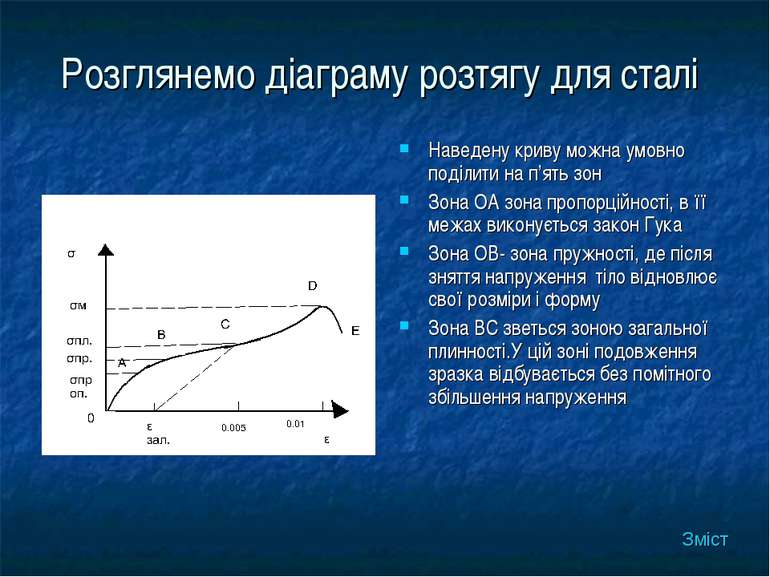
Розглянемо діаграму розтягу для сталі Наведену криву можна умовно поділити на п’ять зон Зона ОА зона пропорційності, в її межах виконується закон Гука Зона ОВ- зона пружності, де після зняття напруження тіло відновлює свої розміри і форму Зона ВС зветься зоною загальної плинності.У цій зоні подовження зразка відбувається без помітного збільшення напруження Зміст

Зона CD-зона зміцнення, у цій зоні подовження зразка супроводжується зростанням напруження, на зразкові з’являється місце майбутнього розриву- шийка, формування якої(точка D)супроводжується процесом місцевої плинності в зоні DE і розривом зразка. σпроп.- найбільше напруження , при якому ще виконується закон Гука. Межа пружності σпр – найбільше напруження, при якому немає залишкових деформацій. Межа плинності σпл.- найбільше напруження, при якому відбувається зростання деформації без помітного збільшення напруження. Межа міцності σм.- найбільше напруження, яке може витримати зразок. Зміст

Деформація біологічних тканин Розглянемо діаграми деформацій тих біологічних тканин і органів, які в процесі функціонування підлягають значним навантаженням- наприклад кісткової, м’язової, сухожилля, стінок судин тощо. Зміст

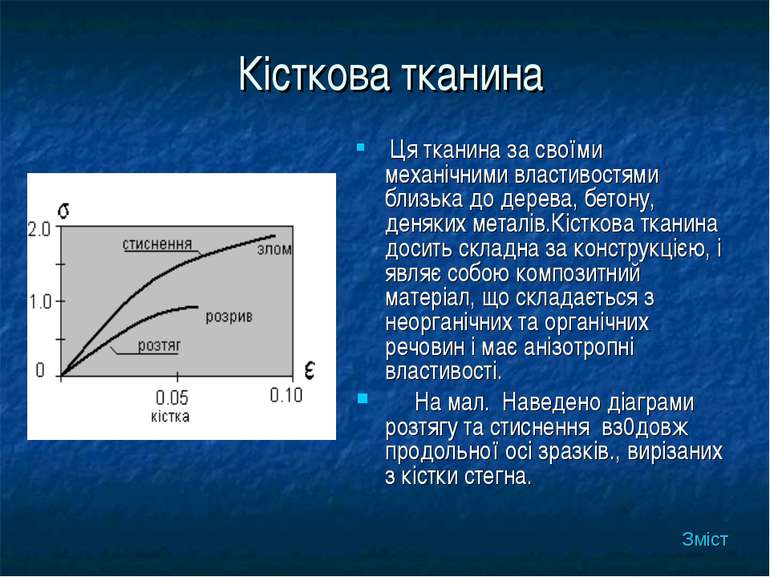
Кісткова тканина Ця тканина за своїми механічними властивостями близька до дерева, бетону, деняких металів.Кісткова тканина досить складна за конструкцією, і являє собою композитний матеріал, що складається з неорганічних та органічних речовин і має анізотропні властивості. На мал. Наведено діаграми розтягу та стиснення вз0довж продольної осі зразків., вирізаних з кістки стегна. Зміст

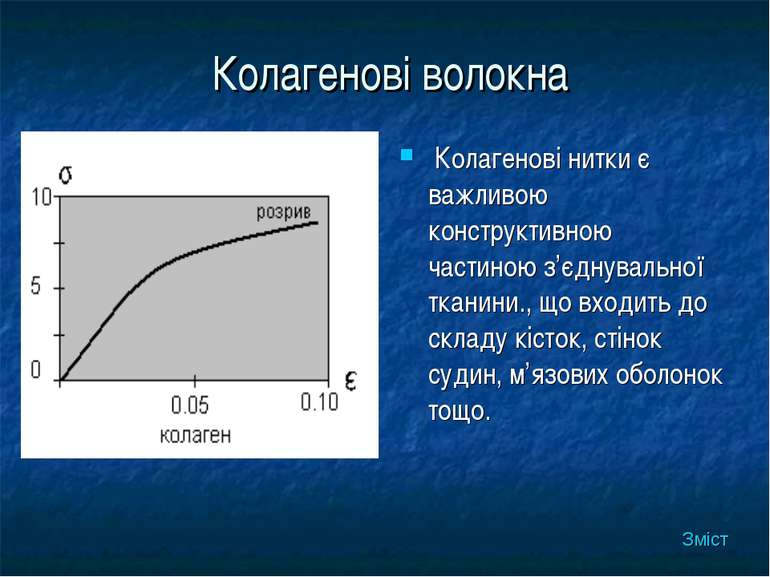
Як бачимо у порівнянні зі сталлю деформація відбувається у значних межах до 10% при стисненні і до 5% при розтязі.При незначних деформаціях(менших за 2%) кістка поводить себе як гуківське тіло.Зауважимо, що кістка краще працює на стиснення , ніж на розтяг- межа міцності та розміри деформацій при стисненні майже вдвічі перевищують ті , що спостерігаються при розтязі. Зміст

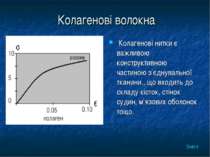
Колагенові волокна Колагенові нитки є важливою конструктивною частиною з’єднувальної тканини., що входить до складу кісток, стінок судин, м’язових оболонок тощо. Зміст

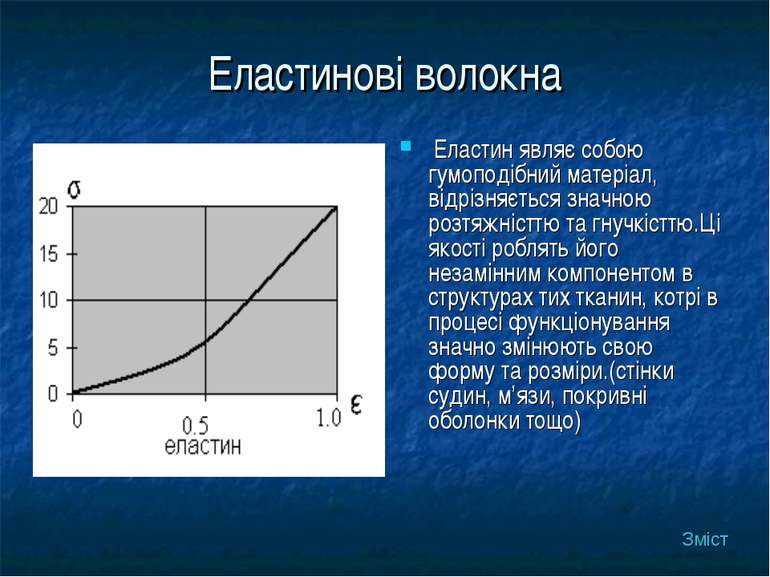
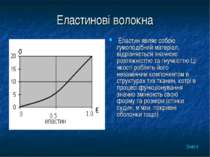
Еластинові волокна Еластин являє собою гумоподібний матеріал, відрізняється значною розтяжністтю та гнучкісттю.Ці якості роблять його незамінним компонентом в структурах тих тканин, котрі в процесі функціонування значно змінюють свою форму та розміри.(стінки судин, м’язи, покривні оболонки тощо) Зміст

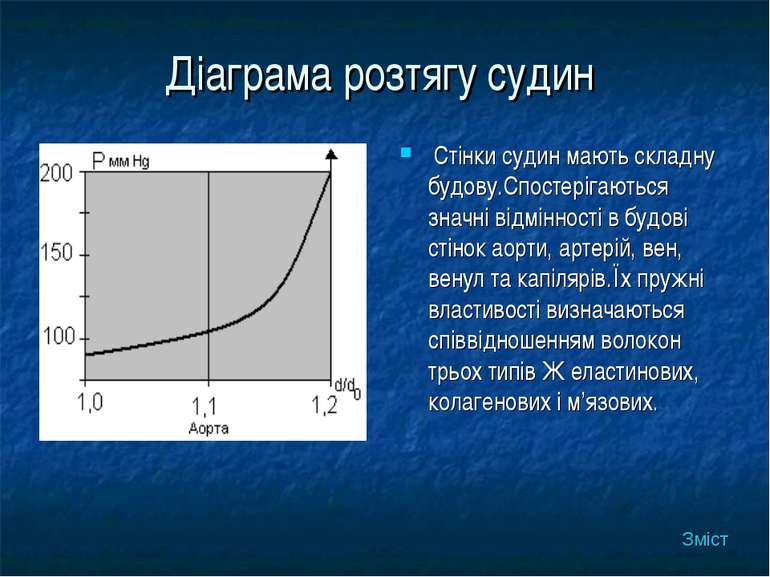
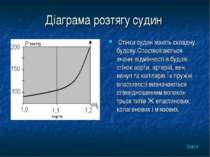
Діаграма розтягу судин Стінки судин мають складну будову.Спостерігаються значні відмінності в будові стінок аорти, артерій, вен, венул та капілярів.Їх пружні властивості визначаються співвідношенням волокон трьох типів Ж еластинових, колагенових і м’язових. Зміст

У великих судинах(аорті, венах) еластин та колаген становлять приблизно 50% сухої ваги, в еластином’язових судинах їх вміст зменшується до 40% і менше. На мал. Розглянуто діаграму розтягу аорти під впливом трансмурального тиску Р(різниці тисків всередині і зовні судини. Зміст

3.2. Плин в’язких рідин у біологічних системах

План Рідкі середовища В’язкість рідини Моделі рідини В’язкість крові В’язко-пружні властивості біологічних тканин Основні рівняння руху рідини Рівняння Бернуллі Пульсові хвилі

Рідкі середовища Рідкі середовища: кров лімфа інтерстиціанальні рідини клітинні рідини Питання План

Рух рідких середовищ у біологічних системах відіграє важливу роль, забезпечуючи умови нормальної життєдіяльності систем. Рідкі середовища мають ряд специфічних можливостей, зумовлених особливостями їх молекулярної будови. План Питання

3.2.1. В’язкість рідини У реальних рідких середовищах на границях шарів, що рухаються, діють сили внутрішнього тертя. План Питання

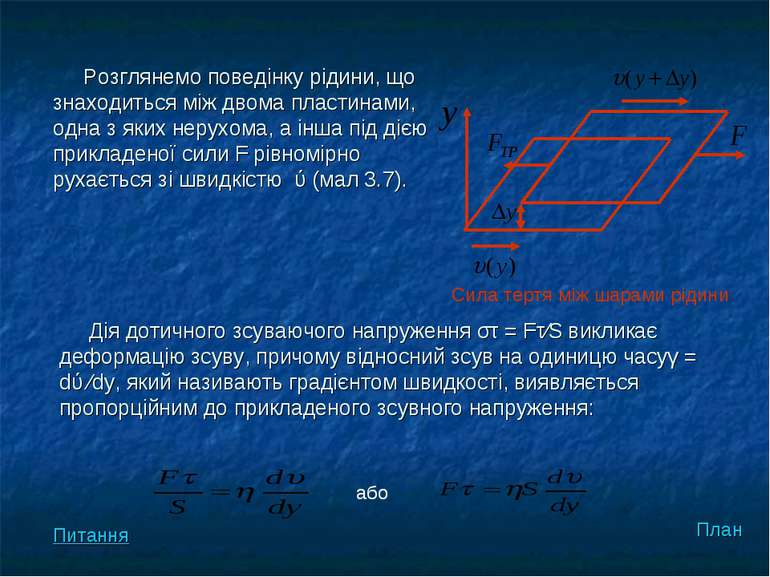
Розглянемо поведінку рідини, що знаходиться між двома пластинами, одна з яких нерухома, а інша під дією прикладеної сили F рівномірно рухається зі швидкістю ύ (мал 3.7). Дія дотичного зсуваючого напруження στ = Fτ∕S викликає деформацію зсуву, причому відносний зсув на одиницю часуγ = dύ ∕dy, який називають градієнтом швидкості, виявляється пропорційним до прикладеного зсувного напруження: План Сила тертя між шарами рідини або Питання

Рівняння (3.8), відоме як рівняння Ньютона, описує явище внутрішньго тертя иіж шарами реальної рідини, що тече, діють сили внутрішньго тертя F, які пропорційні до площі S шарів, що дотикаються, та градієнта швидкості dύ∕dy у напрямку. Перпендикулярному до напрямку плину рідини. Коефіцієнт пропроційності η в рівнянні Ньютона зветься коефіцієнтом в’зкості. План рідина Мал.3.8. Профіль швидкостей Питання

Розмірність фіцієнта в’язкості η у системі СІ [Па·с] Пуаз (П), яка зв’язана з Па·с співвідношенням 1 П = 0,1 Па·с. η води ≈ 1 мПа·с = 1сП. Відносною в’язкістю ηвідн дорівнює відношенню коефіцієнта в’язкості даної рідини до коефіцієнта в’язкості дистильованої води при одній і тій самій температурі: η відн = η /η в Кінематична в’язкість ν рідини, дорівнює відношенню коефіцієнту в’язкості до густини: ν = η /ρ В’язкість рідини є динамічна властивість, залежить від природи рідини, температури і для багатьох рідин також від умов плину. План Питання

Моделі рідини. Модель ідеальної рідини, яка не підлягає стисненню (ρ = const) і в ній відсутні сили внутрішнього тертя (η = 0). Неідеальні рідини, в яких сили внутрішнього тертя описуються рівнянням Ньютона, звуться ньютонівськими. Для ньютонівських рідин коефіцієнт в’язкості η залежить лише від температури та природи рідини і не залежить від умов плину. До ньютонівських рідин можна віднести воду, розчини електролітів, ртуть, гліцерин, спирти. План Питання

Існують рідини, коефіцієнт в’язкості яких залежить від умов плину, а саме, змінюється із зміною швидкості деформації зсуву dύ ∕ dy внаслідок перебудови внутрішньої структури, обумовленої напруженням зсуву при плині рідини – ньютонівські рідини. До них відносять розчини білків, полімерів, деякі суспензії. План Питання

3.2.2. В’язкість крові Кров являє собою приклад складної за своїм змістом рідини. Експеримент виявив суттєву залежність в’язкості кров від її складу, що визначається показником гематокриту Не. Який дорівнює відношенню об’єму форменних елементів Vф до об’му плазми крові Vпл: Показник гематокриту характеризує вміст еритроцитів в крові.В’язкість крові зростає при поліцитемії і зменьшується при анемії. План Питання

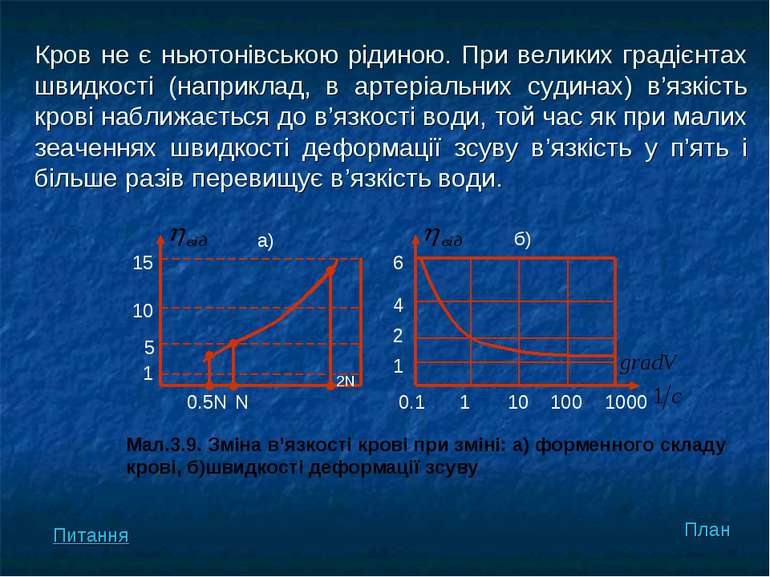
Кров не є ньютонівською рідиною. При великих градієнтах швидкості (наприклад, в артеріальних судинах) в’язкість крові наближається до в’язкості води, той час як при малих зеаченнях швидкості деформації зсуву в’язкість у п’ять і більше разів перевищує в’язкість води. План 0.5N N 0.1 1 10 100 1000 Мал.3.9. Зміна в’язкості крові при зміні: а) форменного складу крові, б)швидкості деформації зсуву Питання

Величина відносної в’язкості крові може бути використана у діагностиці захворювань План Питання Відносна в’язкість крові η відн Результат 4.2 – 6.0 Норма < 2.0 Анемія > 10.0 Поліцитимія

3.2.3. В’язко-пружні властивості біологічних тканин Біологічні структури (м’зи, судини, сухожилля, тканини легенів, шкіра тощо) являють собою в’язко-пружні системи. План Питання

Напруження, що створюються цими елементами під дією зовнішніх сил, дорівнюють: - σn = Eε – для пружного елементу; - στ1 = ηdε/dt – для в’язкого елементу; - στ ~ KFn – для елементу зовнішньго тертя. План Питання

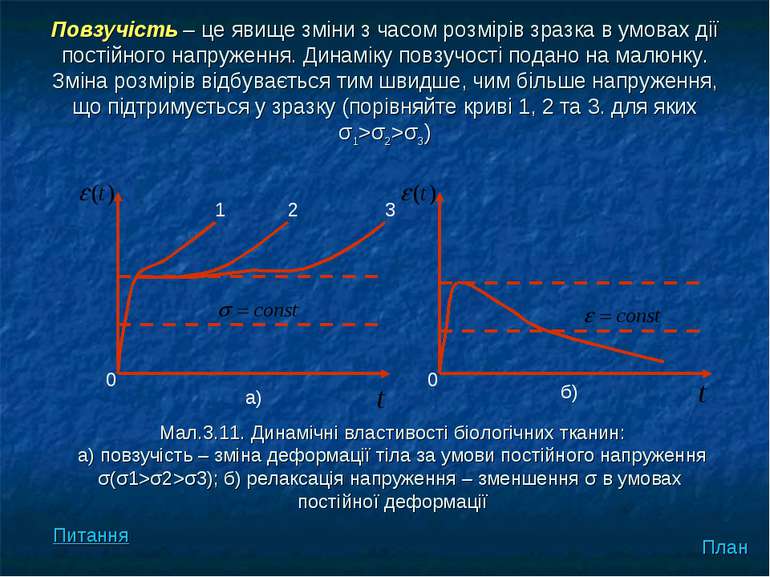
Повзучість – це явище зміни з часом розмірів зразка в умовах дії постійного напруження. Динаміку повзучості подано на малюнку. Зміна розмірів відбувається тим швидше, чим більше напруження, що підтримується у зразку (порівняйте криві 1, 2 та 3. для яких σ1>σ2>σ3) План 1 2 3 0 а) 0 б) Мал.3.11. Динамічні властивості біологічних тканин: а) повзучість – зміна деформації тіла за умови постійного напруження σ(σ1>σ2>σ3); б) релаксація напруження – зменшення σ в умовах постійної деформації Питання

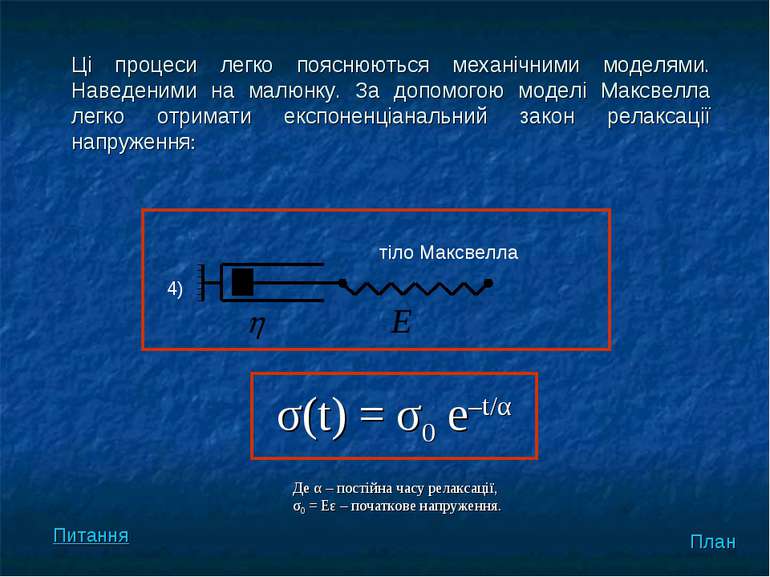
Релаксація напруження – явище зменшення з часом величини напруження у зразку при підтримці постійної величини деформації. Релаксація напруження і повзучість суто динамічні процеси. Ці процеси легко пояснюються механічними моделями. Наведеними на малюнку: План Питання

Ці процеси легко пояснюються механічними моделями. Наведеними на малюнку. За допомогою моделі Максвелла легко отримати експоненціанальний закон релаксації напруження: σ(t) = σ0 e–t/α Де α – постійна часу релаксації, σ0 = Eε – початкове напруження. План 4) тіло Максвелла Питання

Явище повзучості також можна описати експоненціанальним законом: ε(t) = ε0 (1 – e-1/τ) де ε0 = σ0 /Е – початкова деформація, τ – характерний час повзучості, що дорівнює відношенню коефіцієнта в’язкості і модуля Юнга. План Питання

Модель Фойгта дозволяє пояснити поступове зростання з часом напруження у зразку, якщо до тіла прикласти зусилля, що змінюється стрибкоподібно. На цьому ж малюнку наведено одну з найпростіших моделей м’язів, що включає скорочувальний елемент С, який перетворює енергію хімічних реакцій на механічну енергію. Це явище притаманне системам, які адаптуються (зміна тонусу судин). План Питання

3.2.4. Основні рівняння руху рідини Рух рідких середовищ підпорядковується тим самим законам механіки, що і рух твердих тіл та газів. При русі у просторі кожний такий елементарний об’єм рухається вздовж деякої траєкторії – лінії струму. Трубка струму являє собою частину потоку рідини, обмежену лініями струму. План Питання

Поле швидкостей і профіль швидкостей являють собою відповідно значення швидкостей у всіх точках простору і точках перерізу трубки струму у фіксований момент часу. Якщо лінії струму і поле швидкостей не змінюютьсяз часом, торух рідини зветься стаціонарним. При стаціонарному плині траєкторії частинок залишаються незмінними. Якщо поле швидкостей і лінії струму під час плину зникають і знову з’являються, у деяких випадках за формою нагадуютьвихори, такий плин рідини зветься турбулентним або вихровим. План Питання

Рівняння нерозривності струменя Розглянемо стаціонарний плин рідини. Маса рідини, що протікає через цей переріз за одиницю часу, залишається постійною через те, що рідина не розривається і не стикається в звичайних умовах, тобто dm/dt = const. Оскільки dm = Sdl = S·υ·dt, з рівняння отримаємо: ρ·S·υ = const. Для нестислої рідини (ρ = const): S·υ = const, або для різних перерізів трубки струму: S1·υ1 = S2·υ2. План Питання

Величина Q = dV/dt = S·υ [м3/с], що дорівнює об’єму рідини, який протікає через переріз трубки струму заодиницю часу, зветься об’ємною швидкістю плину рідини. Аналогами цієї величини у фізіології є витрата крові або хвилинний об’єм крові (ХОК), хвилинний об’єм крові можна обчислити як відношення ударного об’єму крові Vуд до періоду скорочення Т, обо добуток Vуд на частоту серцевих скорочень ЧСС = 1/T. План Питання

Коли кров постійно рухається по еластичних судинах, внаслідок їх деформації при зміні тиску лінії струму не залишаються постійними. У цьому випадку рівняння нерозривності струменю може бути подано таким чином: де Q1(t) та Q2(t) – відповідно приплив та відток крові для ділянки судини. План Питання

Рівняння Бернуллі. Розглянемо стаціонарний плин ідеальної рідини. Оскільки рідина є ідеальною і робота сил тертя дорівнює нулю, то повна енергія деякого елементу об’єму рідини у цьому випадку буде залишатися величиною сталою при русі вздовж трубки струму: де Ек = Δm·υ2/2 – кінетична енергія, Еп = Δmgh – потенціальна енергія, а Ест = P·ΔV – потенціальна енергія виділенного об’єму рідини. План Питання

Фізичний зміст рівняння Бернуллі полягає в тому, що об’мна густина енергії w ідеальної рідини при її стаціонарному плині залишається величиною сталою. Розмірність об’ємної густини енергії дорівнює: [w] = [E]/[ΔV] = Дж/м3 = Н/м2. Підставляючи ці вирази у формулу і вводячи об’ємну густину енергії w = E/ΔV, отримаємо рівняння Бернуллі, котре являє собою закон збереження енергії для одиниці об’єму рідини, що рухається Рівнянння Бернуллі свідчить про те, що сумарний тиск залишається постійним вздовж трубки струму при стаціонарному плині ідеальної рідини. План Питання

Величина артеріального тиску дозволяє судити про насосну функцію серця й енергію крові на виході серця. Спеціальні регуляторні механізми серця забезпечують саме такий режим скорочення міокарда, за якого при різних навантаженнях серце було б здатне підтримувати на певному рівні об’ємну густину енергії потоку крові, витрачаючи при цьому мінімум хімічної енергії при скороченні міокарда. Насосна функція серця полягає у зміні об’мної густини енергії крові. Насосну функцію серця можна характеризувати різницею об’ємних густин енергії на вході та виході серця, тобто величиною: wс = wарт = wвен План Питання

або для об’ємних сил: Виділимо у рідині елементарний об’єм ΔV циліндричної форми з перерізом S і довжиною Δx. За другим законом Ньютона: Рівняння руху і рівноваги рідини План r R F(x) P1 S mg Fтр x P2 F(x+dx) dx L Мал.3.16.Сили, що діють на елемент об’єму рідини Питання

Проводячи розгляд для y, z-компонент сил, отримаємо: Де – символ градієнта (так званий “оператор набла”). З рівняння випливає, що об’ємна результуюча сила тиску за модулем дорівнює градієнту тиску. Розглянемо сили, що діють на елемент об’єму рідини. Результуюча сила дорівнює тоді як об’ємна сила тиску (сила що діє на одиницю об’єму) є План Питання

Рівняння руху рідини з урахуванням інших об’ємних сил, а саме, сили тертя fmp, сили тяжіння ρg, інших зовнішіх сил fзовн можна у вигляді: План Питання

Отримаємо формулу Пуазейля, яка визначає профіль швидкості ньютонівської рідини в циліндричній трубці Плин в’язких рідин по циліндричних трубках має для медицини особливий інтерес. Плин ньютонівської рідини по горизонтальній трубці. Формула Пуазейля. Визначимо лінійну й об’ємну швидкості плину для стаціонарного потоку в’язкої рідини крізь судину радіусом R, довжиною L, з перепадом тиску на його кінцях P1-P2. План Питання

Дістанемо формулу, що дозволяє визначити об’ємну швидкість рідини: Формула Пуазейля дозволяє визначити об’ємну швидкість плину ньютонівської рідини. Виділимо у перерізі трубки шар рідини товщиною dr і площею dS = 2πrdr. Об’єм рідини, що протікає крізь цю площу за одиницючасу дорівнює План Питання

Формула, що зв’язує між собою об’ємну швидкість рідини і різницю тисків на кінцях судини, має вигляд, аналогічний закону Ома: тому личину W = 8ηL/(πR4) називають гідравлічним опором. Графічні зображення зв’язку Q-ΔP називають діаграмами “витрата-тиск”. План витрата рідини Q різниця тисків 1 2 Мал.3.18. Діаграми “витрата-тиск” для ньютонівської (1) та неньютонівської (2) рідин Питання

3.2.5. Критерії механічної подібності рідин, що рухаються Розглядаючи будь-який плин рідин і рівняння його руху у природі, можна виділити деякі важливі параметри рідини (ρ – густина, χ – модуль об’ємної пружності) і характеристики її руху (υ – швидкість, L – характерні розміри, τ – деякий характерний час, протягом якого відбуваються помітні зміни плину тощо). У гідродинаміці відомі декілька безрозмірних величин, що являють собою комбінацію цих параметрів. Це числа: Рейнольдса (Re), Фруда (F), Маха (M), Струхаля (S). План Питання

Число Маха є відношенням швидкостей рухутіла і звука у даному середовищі: М = υ/с Число Струхаля – відношення деякого характерног розміру потоку рідини і розмірів тіла: S =υ·τ/gL Число Фруда визначає відношення кінетичної енергії рідин до її приросту, обумовленого роботою сили тяжіння на деякій характерній відстані. Ф = υ2/gL Число Рейнольдса дорівнює відношенню кінетичної енергії рідини до витрати її, обумовленої роботоюсил в’язкого тертя на характерній довжині. Відношення кінетичної енергії Ек до роботи А становить число Рейнольдса: Число Рейнольдса визначає відносну роль інерції і в’язкості рідини при її плині. План Питання

Потоки рідин ввіжаються подібними, якщо для них числа Рейнольдса і Фруда збігаються. При малих числах Рейнольдса плин в’язких рідин є ламінарним, при зростанні швидкості ламінарний плин стає нестійким і претворюється в турбулентний. Турбулентний плин – це такий плин, гідродинамічні характеристики якого (швидкість, тиск) різко та нерегулярно змінюються з часом і у просторі. Приклад: кров при вигнанні з шлуночків серця, її плині по аорті тощо. План Питання

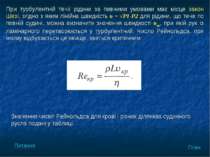
При турбулентній течії рідини за певними умовами має місце закон Шезі, згідно з яким лінійна швидкість υ ~ √P1-P2 для рідини, що тече по певній судині, можна визначити значення швидкості υкр, при якій рух із ламінарного перетворюється у турбулентний. Число Рейнольдса, при якому відбувається це явище, зветься критичним: Значення чисел Рейнольдса для крові і різних ділянках судинного русла подані у таблиці. План Питання

Ще одне застосування преходу між ламінарною і турбулентною течією крові пов’язане з вимірюванням кров’яного тиску методом Короткова. У цьому методі систолічний (верхній) тиск вимірюється у момент, коли кров починає протискуватися через отвір в артерії, стиснутий за допомогою манжети. Саме у цей момент виникають шуми, обумовлені появою турбулентної течії крові. Діастолічний (нижній) тиск фіксується у момент, коли ці шуми зникають внаслідок послаблення манжети і переходу течії від ламінарної до турбулентної. Якщо число Рейнольдса стає більшим за своє критичне значення і виникає перехід від ламінарного плину крові до турбулентного (анемія). План Питання

Походження пульсових хвиль пов’язане з реакцією пркжних стінок судини на пульсуючий плин крові, що виникає при періодичній роботі серця. 3.2.6. Пульсові хвилі План Питання

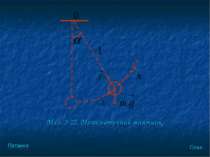
Розглянемо спрощену модель появи пульсових хвиль в еластичній судині Виділимо невелику ділянку еластичної судини, на одному з кінців якого знаходиться поршень. На поршень короткочасно діє сила F. Рідина біля поршня внаслідок її інерції не встигає преміститися вздовж судини, дія сили викликає зростання тиску на стінку – ділянка розширюється доти, доки напруження стінки не компенсує зростання тиску всередині судини. Процес повторюється після нового поштовху поршня. По еластичній судині поширюється хвиля. План Питання

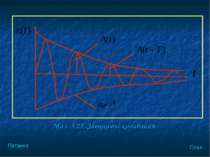
Запишемо рівняння пульсової хвилі. Позначимо зіну радіуса ділянки трубки при розширенні через ε, тоді поточне значення радіуса дорівнюватиме Рівняння пульсової хвилі, яке характеризує процес розповсюдження зміни радіуса судини ε вздовж її осі має такий вигляд: План Питання

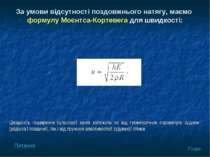
За умови відсутності поздовжнього натягу, маємо формулу Моєнтса-Кортевега для швидкості: Швидкість поширення пульсової хвилі залежить як від геометричних параметрів судини (радіуса і товщини), так і від пружних властивостей судинної стінки. План Питання

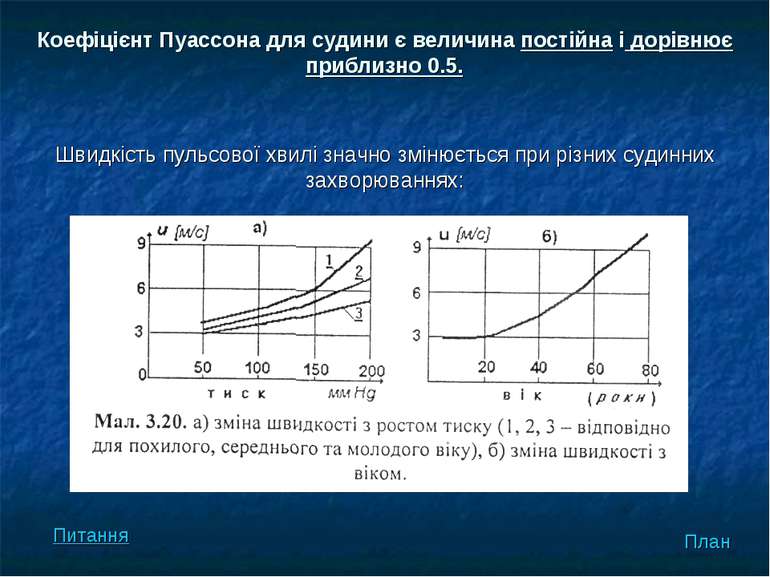
Швидкість пульсової хвилі значно змінюється при різних судинних захворюваннях: Коефіцієнт Пуассона для судини є величина постійна і дорівнює приблизно 0.5. План Питання

Рух крові по серцево-судинній системі досить складне явище. У таблиці наведено деякі показники системи кровообігу в стані спокою і при навантаженні. План Питання № Праметри системи кровообігу Значення 1. Середня лінійна швидкість в аорті в капілярі у вені 0.3-0.4 м/c 0.002-0.01 м/c 0.2-0.4 м/c 2. Середній артеріальний тиск -спокій -максимальне навантаження 90-100 мм рт. ст. вище за 200 мм. рт.ст. 3. Середній тиск у капілярах 25-30 мм рт. ст. 4. Хвилинний об’єм крові -спокій -максимальне навантаження 5-6 л/хв Вище за 20 л/хв 5. Швидкість пульсової хвилі (артерія) 4-6 м/c 6. Число Рейнольдса в аорті у вені в капілярах 3000-4000 500-700 0.001 7. Площа перерізу - аорти - капілярів

Питання Що таке в’язкість рідини? Які існують моделі рідини? Які рідини називають ньютонівськими? Чому кров не є ньютонівською рідиною? Явище повзучості – що це таке? Що являє собою релаксація напруження? Що таке насосна функція серця? Формула Пуазейля –сформулювати. Які існують механічні критерії рідин, що рухаються? Що являють собою пульсові хвилі? План

3.3. Механічні коливання стор. 205 - 219

ЗМІСТ 3.3. Механічні коливання 3.1.1. Гармонiчнi коливання та їх основнi параметри Швидкiсть та прискорення при гармонічних коливаннях Перiод i частота гармонiчних коливань 3.3.2. Затухаючi коливання і аперiодичний Рух

3.3.3. Вимушені коливання 3.3.4. Явище резонансу i автоколивання Додавання гармонічних коливань 1. Додавання гармонiчних коливань, снрямованих вздовж однієї нрямої 2. Додавання взаемноперпендикулярних гармонiчних коливань Контрольні питання

3.3. МЕХАНIЧНI КОЛИВАННЯ (стр. 205-219)

Багатьом процесам, що вiдбуваються в бiологiчних системах, властива перiодичнiсть. Вона спостерiгається у функцiональнiй дiяльностi серця, легенiв, шлунка. План Питання

Деякi процеси у живих органiзмах можна вважати коливальними: коливання стiнок, судин при поширення пульсових хвиль, коливання тиску кровi у судинах, об’єму повiтря у легенях, коливання барабанних перетинок, голосових зв’язок, значень бiопотенцiалiв у рiзних точках тiла людини. План Питання

Для визначення норми або патології того чи iншого органа застосовують графiчний запис перiодичних процесiв, якi супроводжують його функцiональну дiяльнiсть, з подальшим його аналiзом - визначенням його тривалостi (перiоду), частоти й амплiтуди дослiджуваних величин. План Питання

Для розв’язання подiбних задач необхiдне знання загальних закономiрностей, що притаманнi коливальним процесам незалежно вiд їх природи i що описуються єдиними математичними рiвняннями. Закономiрностi, властивi коливальним процесам, найбiльш просто вивчати на прикладi механiчних коливань. План Питання

3.1.1. Гармонiчнi коливання та їх основнi параметри План Питання

Розглянемо пружинний маятник (мал. 3.21). При змiщеннi матерiальної точки масою т на вiдстань х вiдносно положення рiвноваги на неї починає дiяти сила пружностi, яка викликана деформацiєю пружини План Питання

Fпр = - kx. Мал. 3.21. Пружинний маятник. (3.35) План Питання

Згiдно з II законом Ньютона ця сила надаватиме матерiальнiй точцi прискорення: Fпр = mα. Прирiвнюючи правi частини рiвностей (3.35) i (3.36), одержимо: mα =-kx (3.36) (3.37) План Питання

Враховуючи, що прискорення є другою похiдною вiд координаты за часом а =х, останнє рiвняння набуває вигляду лiнiйного диференцiйного рiвняння mx + kx=0 (3.38) План Питання

Оскiльки коефiцiєнт жорсткостi пружини k > 0 i т > О, вiдношення k/m можна позначити через квадрат деякої величини : = k/m (3.38) Тодi рiвняння (3.38) матиме вигляд: X+ =0 (3.39) План Питання

Таким чином, функцiя x =f(t) задовольняс диференцiйному рiвнянню II-го порядку, яке с лiнiйним, однорiдним i зi сталими коефiцiснтами. Розв’язок таких рiвнянь, як вiдомо, зводиться до розв’язування вiдповiдних характеристичних алгебраїчних рiвнянь. План Питання

Складемо характеристичне рiвняння, що вiдповiдає диференцiйному рiвнянню (3.39): + =0 (3.40) Коренi цього квадратного рiвняння дорiвнюють , тобто вони є рiзними й уявними. План Питання

Загальний розв’язок диференцiйного рiвняння (3.39) на випадок таких коренiв вiдповiдного характеристичного рiвняння має вигляд: Нехай а де А та - довільні сталі, тоді План Питання

Якщо покласти а то прийдемо до результату: (3.42) Значения сталих А та визначаються початковими умовами, тобто положениям та швидкiстю матерiальної точки в момент часу t=0 План Питання

Отже, ми дiйшли до висновку: матерiальна точка, що знаходиться під дiєю пружної сили, здiйснює коливальний рух, при якому її змiщення вiд положення рiвноваги змiнюється з часом за законом синуса або косинуса. Такi коливання називають гармонiчними. План Питання

Стала А в рiвняннях (3.42) є амплiтуда гармонiчного коливання, вона дорiннює максимальному змiщенню маятника вiд положення рiвноваги. Аргумент синуса (або косинуса): — фаза коливань. План Питання

Фаза визначає змiщення маятника в будь-який момент часу, — початкова фаза, яка визначає змiщення маятника в момент часу t= 0. Величина — циклiчна частота коливань. План Питання

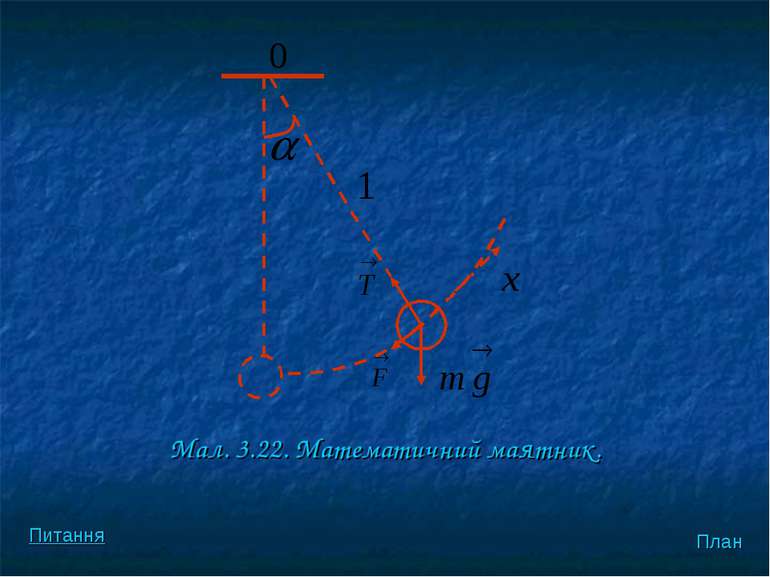
Тiй же самiй закономiрностi пiдпорядковується змiщення вiд положення рiнноваги математичного маятника, що коливається, при невеликих кутах вiдхилення а (мал. 3.22). План Питання

Мал. 3.22. Математичний маятник. План Питання

Сила, яка спричиняє коливання математичного маятника, не є пружна за своєю природою. Дiйсно, повертаюча сила F спрямована по дотичнiй до дуги кола радiуса l, напрямлена до положення рiвноваги i пропорцiйна зміщенню х: (оскiльки для малих кутiв a маємо ). План Питання

Сила, що не є пружною за своєю природою, але аналогiчна їй по залежностi вiд змiщення, називається квазiпружною. Таким чином, F є квазiпружною силою. Рiвняння динаміки для математичного маятника матиме вигляд: (3.43) , або , План Питання

Отримане рiвняння повнiстю збiгасться з рiвнянням (3.41), що описує рух пружного маятника, а отже має той самий розв’язок. Таким чином гармонічні коливання — це коливання, що вiдбуваються пiд дiєю пружних або квазiпружних сил. План Питання

Швидкiсть та прискорення при гармонічних коливаннях. План Питання

Нехай вiдлiк часу обрано таким чином, щоб початкова фаза . Тодi розв’язок рiвняння (3.41) матиме вигляд: (3.44) План Питання

Швидкiсть тiла, шо коливається, знайдемо як похiдну вiд координати х за часом t. (3.45) де — амплiтуда швидкості. План Питання

З рiвнянь (3.43) та (3.44) випливає, що швидкiсть також змiнюється за гармонiчним законом, а фаза швидкостi вiдрiзаяється вiд фази змiщення на /2, тобто в момент часу. коли х = 0, шнидкiсть максимальна. План Питання

Оскiлъки швидкiсть при гармонiчних коливаннях змiнюється з часом, то цей рух характеризується прискоренням, яке знайдемо як другу похiдну вiд змiщення х за часом План Питання

(3.46) де — амплiтуда прискорення. План Питання

Видно, що i прискорення змiнюється за гармонiчним законом, а фаза прискорення вiдрiзняється вiд фази змiщення на , а вiд фази швидкостi на, /2. Замiнивши в (3.46) через х, отримасмо: План Питання

З цiєї рiвностi виходить, що при гармонiчних коливаннях прискорення тiла прямо пропорцiйне до змiщення вiд положення рiвноваги i має протялежний змiщенню налрямок. План Питання

Перiод i частота гармонiчних коливань. План Питання

Перiодом гармонiчного коливального руху називають найменший промiжок часу T, по закiнченнi якого всi величини, що характеризують цей рух (х, v, а), набувають первiснi значення. З рiвностей (3.44) — (3.46) випливає, що перiоду коливань вiдповiдає змiна фази на величину 2 . План Питання

У момент часу t фаза дорiвнює , а в момент часу t+T: . Тодi з умови перiодичностi маємо: (3.47) План Питання

Пiдставляючи в (3.47) вирази для , що вiдповiдають пружинному та математичному маятникам, отримаємо вiдповiднi вирази для перiодiв коливань цих маятникiв: (3.48) План Питання

Величину називають частотою коливань. Частота вказує, скiльки разiв за 1 сек. повторюється один i той же стан тiла, що коливається. Частота вимiрюється в Герцах (Гц), План Питання

Розглянутi коливання вiдбуваються при вiдсутностi сил тертя i зовнiшніх сил. Такi коливання називають власними. Частота (перiод) власних коливань, як випливає з (3.48), залежить лише вiд властивостей самої системи. План Питання

3.3.2. Затухаючi коливання і аперiодичний Рух План Питання

Припустимо, що в розглянутих системах iснусє тертя чи опiр, причому сила тертя (опору) пропорцiйна швидкостi: , де r — коефiцiєнт тертя (опору). Запишемо в цьому випадку рiвняння руху (II закон Ньютона). або План Питання

Позначивши , , отримаємо диференцiйне рiвняння другого порядку, що описує рух пружинного маятника у присутностi сил тертя (3.49) План Питання

Складемо характеристичне рiвняння, що вiдповiдає диференцiйному рiвнянню (3.49): Знайдемо коренi характеристичного рiвняння (3.50) План Питання

Загальний розв’язок рiвняння (3.49) залежить вiд знака рiзницi . Розглянемо всi можливi випадки: План Питання

1. , коли коренi характеристичного рiвняння є комплексними числами (затухаючi коливання) де — циклiчна частота. План Питання

У випадку комплексних коренiв характеристичного рiвняння загальний розв’язок (3.49) має вигляд (3.51) або План Питання

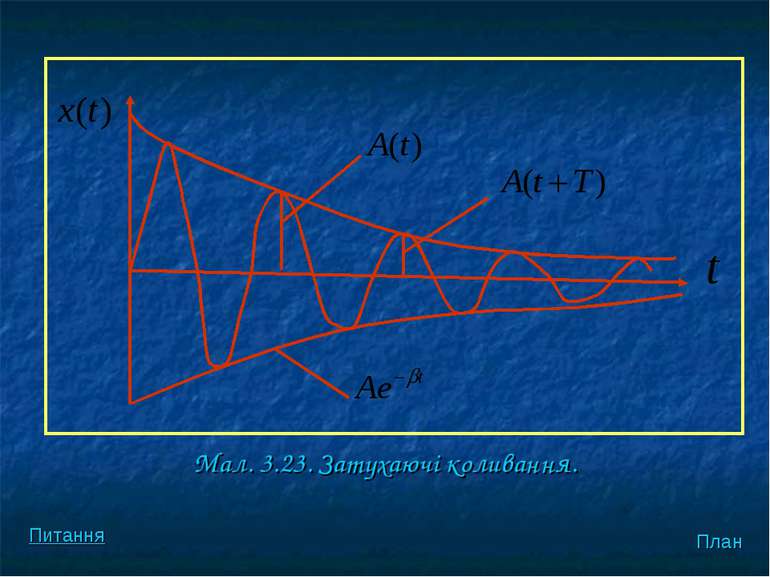
Де — ампдiтуда коливань, яка зменшується за експоненцiальним законом, - коефiцiент затухання, визначас швидкiсть затухання амплiтуди. Залежнiсть x=f(t) для затухаючих коливань подано на мал. 3.23. План Питання

Мал. 3.23. Затухаючi коливання. План Питання

Ступiнь затухання часто характеризують декрементом затухання i логарифмiчним декрементом затухання : , де перiод затухаючих коливань дорiвнює План Питання

2. , коли коренi характеристичного рiвняння є дiйсними числами (аперiодичнi коливання) План Питання

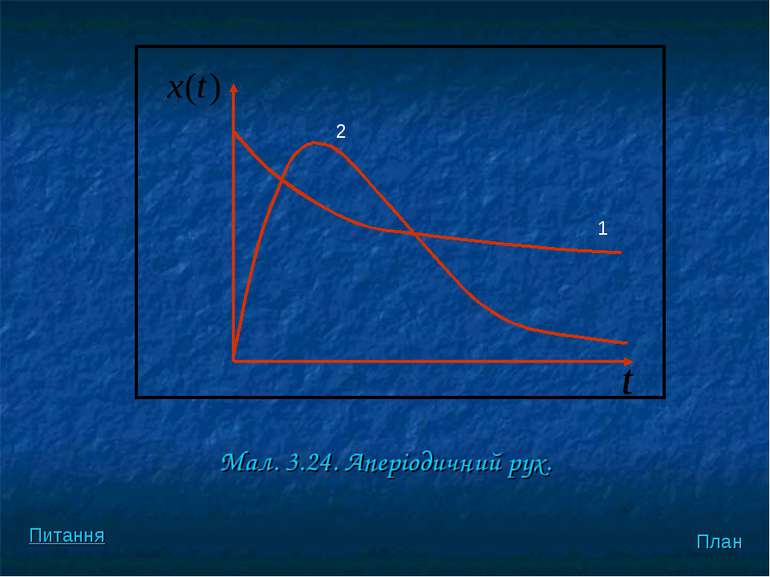
У цьому випадку загальний розв’язок рiнняння (3.49) матиме вигляд (3.52) що вiдповiдає аперiодичному руховi (мал. 3.24). План Питання

Мал. 3.24. Аперiодичний рух. 2 1 План Питання

3. , коли коренi є кратними. Легко побачити, що i в цьому випадку рух тiла буде аперiодичним. Коливання, що виника юты у системi при вiдсут ностi зовнi сил, нази iзають вiльними. План Питання

Частота вiльних коливань залежить як вiд пружних властивостей системи ( ), так i вiд iнтенсивностi втрат ( ). План Питання

Якщо , то і перiод вiльних коливань стає близьким до перiоду власних коливань (мал. 3.23). План Питання

3.3.3. Вимушені коливання План Питання

Припустимо, що на матерiальну точку масою т, крiм вружної або квазiпружної сили i сили тертя, дiє зовнiшня вимушуюча сила, що змiнюється за перiодичним законом де -амплiтуда, а -циклiчна частота вимушуючої сили. План Питання

В цьому випадку рiвняння руху матиме вигляд або (3.53) План Питання

Загальний розв’язок диференцiйного рiвняння (3.53) має вигляд (3.54) де А — амплiтуда вимушених колитвань, яка дорівнює (3.55) План Питання

А початкову фазу визначають з рiвностi: (3.56) План Питання

Важливу формулу (3.55) для амплiтуди А вимушених коливань можна отримати, скориставшись графiчним методом розв’язку неоднорiдних диференцiйних рiвнянь 2-го порядку з постiйними коефiцiснтами. План Питання

З формули (3.54) для змiщення х легко отримати вирази для похiдних План Питання

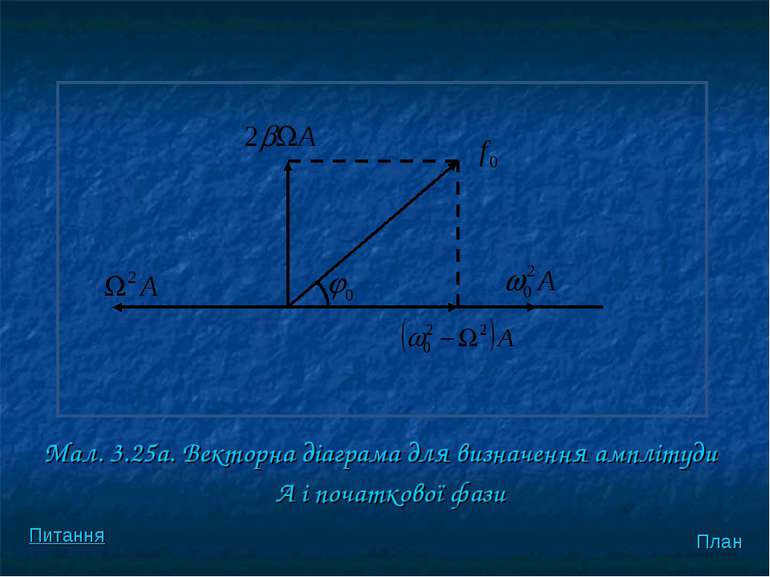
Якщо намалювати „векторну” або “фазову” дiаграму (мал. 3.25а), вiдклавши на нiй амплiтуднi значення всiх доданкiв у рiвняннi (3.53) з урахуванням зсуву їх фаз. План Питання

То очевидно, що векторна сума трьох доданкiв у лiвiй частинi (3.53) повинна дорiвнювати амплiтудному значенню вимушуючої сили, тобто План Питання

Звiдси безпосередньо випливас формула (3.55) для амплiтуди А, так само як i формула (3.56) для . План Питання

Мал. 3.25а. Векторна діаграма для визначення амплітуди А і початкової фази План Питання

Таким чином, якщо на тiло, яке коливасться, дiє зовнiшня перiодична сила з частотою , то тiло здiйснює коливання з тiєю ж частотою , причому амплiтуда коливань залежить вiд амплiтуди i частоти зовнiшньої сили, вiд коефiцiєнта затухання, вiд пружних властивостей системи i маси тiла, яке коливається. Такi коливання називають вимушеними. План Питання

3.3.4. Явище резонансу i автоколивання План Питання

Явище досягнення максимальної амплiтуди вимушених коливань при заданих i називають резонансом. Явище резонансу спостсрiгається при такiй частотi вимушуючої сили, при якiй амплiтуда вимушених коливань А досягає максимального значення. План Питання

Вiдповiдно до формули (3.55) дослiдження функції на екстремум дає рiвнянн , яке дозволяє отримати значення резонансної частоти: План Питання

Цьому значенню резонансної частоти вiдповiдає значення резонансної максимальної амплiтуди За вiдсутностi затухання : , а План Питання

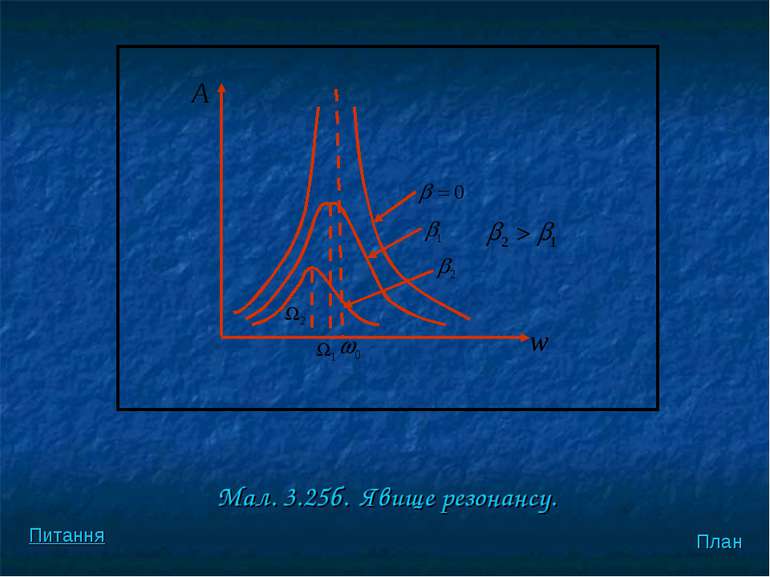
На мал. 3.25б поданi резонанснi кривi — залежностi амплiтуди вимушених коливань вiд частоти змушуючої сили при рiзних коефiцiєнтах затухання . План Питання

Мал. 3.25б. Явище резонансу. План Питання

При вимушених коливаннях подача енергiї ззовнi (для компенсацiї втрат на тертя) здiйснюється i регулюється зовнiшньою перiодичною силою, яка нав’язує системi свою частоту i визначає амплiтуду коливань. Однак, можна викликати незатухаючi коливання i постiйною силою, якщо сама система буде регулювати подачу енергiї ззовнi. План Питання

Системи, якi автоматично регулюють подачу енергiї вiд зовнiшнього джерела, називають автоколивальними, а перiодичнi процеси, якi в них вiдбуваються, автоколиваннями. Амплiтуда i частота автоколивань залежать вiд властивостей самої системи. План Питання

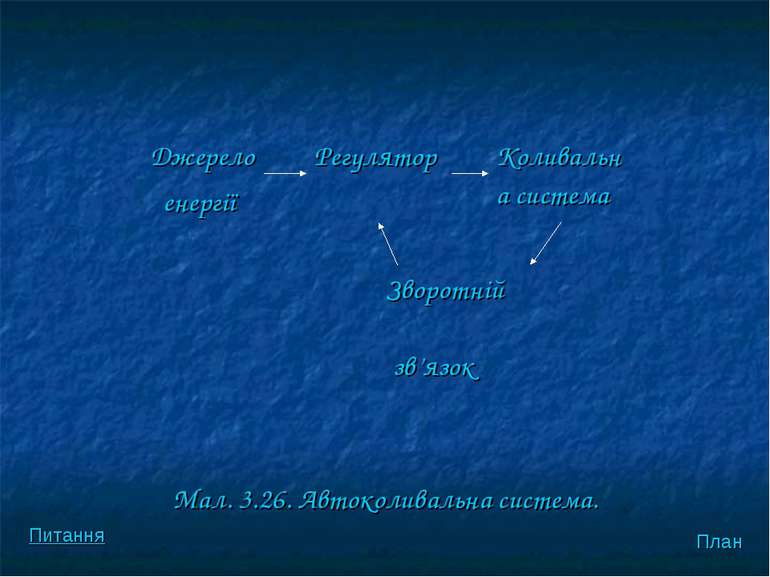
Схему автоколивальної системи, яка складається з чотирьох обов’язкових елементiв, подано на мал. 3.26. План Питання

Мал. 3.26. Автоколивальна система. План Питання Джерело енергії Регулятор Коливальна система Зворотній зв’язок

Прикладами автоколивальних систем є: План Питання

Годинник (маятник — коливальна система, пiднесена гиря або пружина — джерело енергiї, анкер—регулятор надходження енергiї вiд джерела в коливальну систему, який зв’язаний з коливальною системою зворотнім зв’язком). Генератор електромагнiтних коливань. Серце, легенi — бiологiчнi автоколивальнi системи. План Питання

Форма автоколивань може бути рiзною: це можуть бути коливання, що наближаються до гармонiчних (маятниковий годинник, коливання в LС-генераторах), або iмпульснi коливання рiзної форми — прямокутнi, експоненцiальнi, пилкоподiбнi. План Питання

3.3.5. Додавання гармонiчних коливань План Питання

Коливання, для котрих змiщення як функцiя часу може бути описано будь-яким законом, окрiм синуса чи косинуса, називають складними (негармонiчними).

Вiдомо, що будь-яке складне коливання можна подати у виглядi суми простих гармонiчних коливань. Перш нiж аналiзувати складнi коливання (а таку задачу медикам доводиться розв’язувати досить часто), розглянемо, до яких результатiв може призвести додавання гармонiчних коливань. План Питання

1. Додавання гармонiчних коливань, снрямованих вздовж однієї нрямої План Питання

Нехай тiло бере участь одночасно у двох коливаннях, спрямованих вздовж однiєї прямої, причому амплiтуди i перiоди (частоти) цих коливань однаковi, а початковi фази рiзнi План Питання

Результуюче змiщення х тiла вiд положення рiвноваги дорiвнює алгебраїчнiй сумi змiщень i : де , План Питання

Таким чином, результуюче коливання являє собою гармонiчне коливання, яке вiдбувається вздовж тiєї ж самої прямої, що i складовi коливання, i з перiодом (частотою), який дорiвнює перiоду (частотi) складових коливань. План Питання

Амплiтуда результуючого коливання залежить вiд рiзницi початкових фаз складових коливань. План Питання

Якщо , де k=0,1,2,3…, то i (або , якщо . Якщо , то і (або , якщо ) План Питання

Якщо складовi коливання вiдрiзняються перiодами (частотами), то результуюче коливання вже не буде гармонiчним. План Питання

Розглянемо, як особливо цiкавий, результат додавання двох гармонiчних коливань рiвних амплiтуд i фаз, перiоди (частоти) яких вiдрiзняються, тобто План Питання

Результуюче змiщення дорівнює Де , План Питання

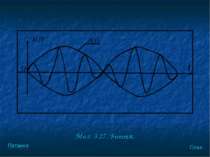
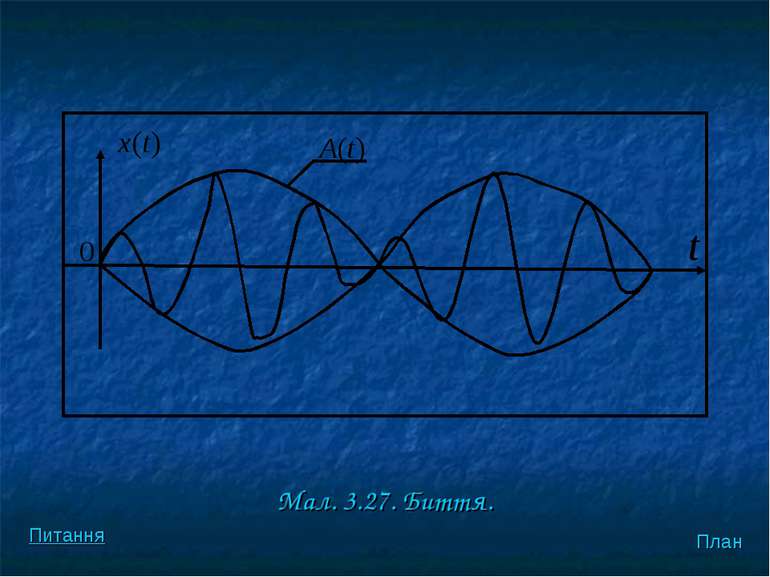
Якщо різниця мала, то амплітуда А(t) змінюється з часом гармонічним законом, але з частотою . Такі коливання називають биттям. (Мал. 3.27). План Питання

Мал. 3.27. Биття. План Питання

Перiод змiни амплiтуди коливань називають перiодом биття (Tб). Перiод биття може бути визначений з умови: , План Питання

Отже, частота Таким чином, частота змiни амплiтуди результуючого коливання дорiвнює рiзницi частот складових коливань. План Питання

2. Додавання взаемноперпендикулярних гармонiчних коливань План Питання

Нехай матерiальна точка водночас бере участь у двох коливаннях, що вiдбуваються у взаємно перпендикулярних напрямках: План Питання

Сукупнiсть координат х i у матерiальної точки у рiзнi моменти часу визначають траєкторiю руху матеріальної точки у площинi ХУ. Форма траєкторiї залежить вiд спiввiдношення частот i рiзницi фаз складових коливань. План Питання

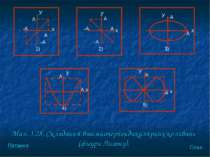
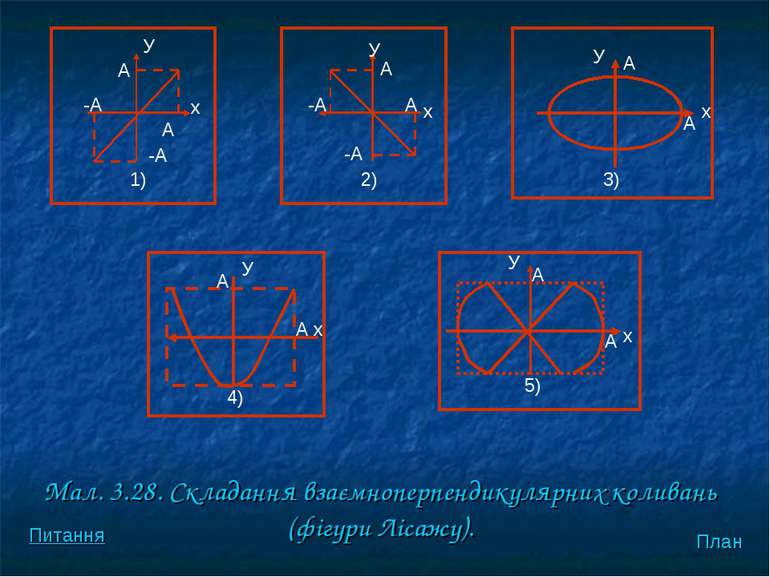
Наведемо деякi випадки додавання коливань (мал. 3.28): 1) , рiвняння траєкторiї 2) , рiвняння траєкторiї План Питання

3) , рiвняння траєкторiї 4,5) , у цьому випадку форма траєкторiї залежить вiд спiввiдношення частот і . План Питання

На мал. 3.28 наведено траєкторії для випадкiв i . План Питання

Мал. 3.28. Складання взаємноперпендикулярних коливань (фiгури Лiсажу). 1) A x -A A -A У -A -A 2) A A x У У A x A 3) A У A x 4) У A x A 5) План Питання

Отриманi кривi, що iх описує матерiальна точка, називають фiгурами Лiсажу. Кривi, подiбнi до кривих Лiсажу, спостерiгають при дослiдженнi бiопотенцiалiв серця методом векторелектрокардiографiї. План Питання

Контрольні питання до теми: МЕХАНІЧНІ КОЛИВАННЯ

Що таке квазіпружна сила? Що називають періодом гармонічного коливального руху? Що таке явище резонансу і де воно спостерігається? Які періодичні процеси відбуваються в автоколивальних системах? Від чого залежить амплітуда регулюючого коливання? План

ІІ Закон Ньютона Прискорення, що надається тілу певною силою прямопропорційне цій силі і оберненопропорційна масі тіла. Назад

Сторінки 219-222 Механічні хвилі

Пружні сили Розповсюдження деформації Механічна хвиля. Описання Види хвиль Фазова поверхня Швидкість розповсюдження хвилі Потік енергії хвилі. Вектор Умова Перевір себе ЗМІСТ

Якщо тіло, яке коливається, знаходиться у пружному середовищі, то у ділянках середовища, що прилягають до тіла, виникають періодичні деформації, які зумовлюють появу пружніх сил. План Питання

Завдяки взаємодії частинок середовища деформації будуть розповсюджуватись з деякою швидкістю, яка залежить від фізичних властивостей середовища. При цьому частинки середовища здійснюють коливальний рух навколо положення рівноваги, а від одних ділянок середовища до інших передається лише стан деформації План Питання

- Процес розповсюдження коливального руху в середовищі Цей процес можна описати через зміну в часі і просторі положення частинок середовища ( зміну величини зміщення S (x, t), тиску P(S, t), або густини ρ (x, t)). План Питання

поздовжні поперечні Частинки коливаються вздовж лінії розповсюдження коливань. Ці хвилі збуджуються в середовищах, в яких пружні сили виникають при деформаціях стиснення і розтягування, тобто в газах, рідинах, твердих тілах. Частинки середовища здійснюють коливання в напрямку, перпендикулярному до напрямку розповсюдження хвилі. Такі хвилі збуджуються в середовищах, в яких пружні сили виникають при деформаціях зсуву (твердих тілах). Хвилі План Питання

Це геометричне місце точок, які коливаються в однаковій фазі. Поверхня, до якої надійшла хвиля у деякий момент часу, називається фронтом хвилі Якщо х = const, то хвиля зветься плоскою В ізотропному середовищі від точкового джерела розповсюджується сферична хвиля, в якої хвильова поверхня є сфера План Питання

Під швидкістю розповсюдження хвилі розуміють швидкість розповсюдження фіксованої фази коливання. Дійсно, якщо ω (t – x / v) = const. З рівняння плоскої хвилі випливає, що хвиля має подвійну періодичність (як у просторі, так і у часі). План Питання

Потік енергії через дану поверхню – це кількість енергії, що переноситься хвилею через поверхню S за одиницю часу. Нехай за час ∆t фронт хвилі змістився на відстань ∆l = v∆t. Отже, за час ∆t всі частинки середовища в об’ємі ∆V=S∆l отримали енергію ∆E = ωS∆L, яка пройшла через площину S за час ∆t, де ω – об`ємна густина енергії. Потік енергії, який переноситься хвилею через одиничну поверхню в напрямку нормалі до цієї поверхні, називається густиною потоку енергії, або інтенсивністю хвилі

Інтенсивність хвилі І – векторна величина, оскільки швидкість v – вектор, саме тому її називають вектором Умова Вектор Умова чисельно дорівнює густині потоку енергії і збігається за напрямком з вектором швидкості розповсюдження хвилі. Об’ємну густину енергії ω можна знайти як сумарну енергію коливань всіх n частинок в одиниці об’єму.

Що зумовлює пружні сили ? Як розповсюджується деформація? Що таке механічна хвиля? Як описується цей процес? Види хвиль. Охарактеризуйте кожен вид хвилі. Що називають фронтом хвилі? Що розуміють під швидкістю розповсюдження хвилі? Що таке густина потоку енергії? Що таке вектор Умова? Охарактеризуйте його. План

Акустика. Елементи фізики слуху. Основи аудіометрії. (стр.223-237)

План Акустика – наука про звук Звук Об’єктивні характеристики звуку Орган слуху Суб’єктивні характеристики слухового відчуття Аудіаметрія Ультразвук Інфразвук Питання

Акустика – наука про звук. Предмет акустики - вивчення фізичної природи звуку, механізмів його генерації, розповсюдження (заломлення, відбивання, поглинання) План Питання

Звук – частинний випадок механічних хвиль з частотою в інтервалі від 16 до 20000 Гц. 16 Гц – інфразвук 20 103 Гц 109 Гц – ультразвук 109 Гц – гіперзвук. План Питання

Застосування в медицині: аускультація та перкусія; фонокардіографія; застосування ультразвуку (для діагностики та лікування) План Питання

Всі звуки поділяються на: тони (музикальні звуки); шуми; звукові удари. План Питання

Тони (музикальні звуки) обумовлені коливаннями джерела з постійною амплітудою та частотою, або такими, що закономірно змінюються у часі. Розрізняють: прості, викликані гармонічними коливаннями джерела (звук камертона); складні, викликані ангармонічними коливаннями, які можуть бути розкладені на прості (голос людини, звуки музичних інструментів). План Питання

Основна характеристика простого тону – частота. Основний тон – тон, який входить до складного і має найменшу частоту ( о). Обертони – прості тони, що входять до складного і мають частоти, кратні частоті обертону ( = n о, де n = 1,2, ...). План Питання

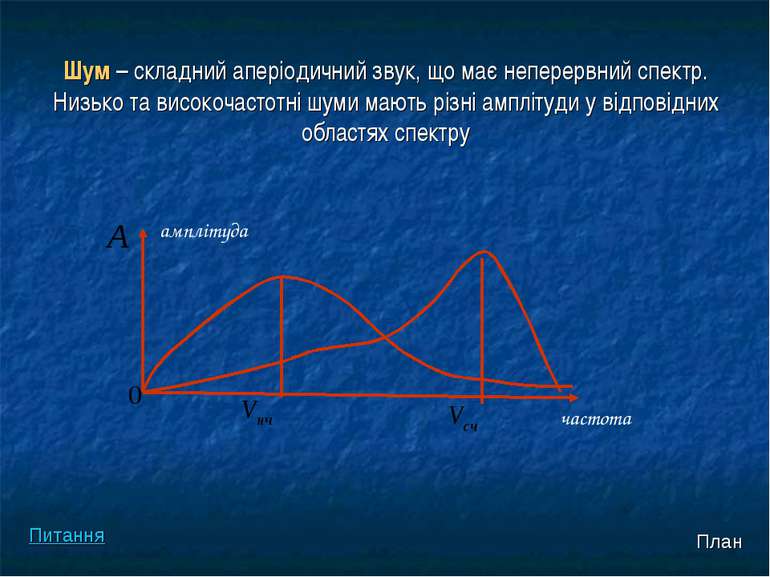
Шум – складний аперіодичний звук, що має неперервний спектр. Низько та високочастотні шуми мають різні амплітуди у відповідних областях спектру амплітуда частота План Питання

Звуковий удар – це короткочастотний звук, що має неперервний спектр (вибух).   План Питання

Основні характеристики звуку: (об’єктивні характеристики, можуть бути виміряні приладами незалежно від людини). Інтенсивність або сила звуку; Частота; Частотний спектр. План Питання

Інтенсивність звуку – густина потоку енергії, що її приносить звукова хвиля, тобто Інтенсивність звуку називають також силою звуку, тому що інтенсивність визначає надлишковий звуковий тиск ( Р), що виникає у ділянках згущення частинок при розпов-сюдженні звукової хвилі: План Питання

Людське вухо сприймає досить великий діапазон інтенсивностей звукової хвилі. На частоті 1 кГц - найменша інтенсив-ність, що спириймається, в середньому становить: Іmin = Іо= 10–12 Вт/м2 (поріг чутності); а найбільша: Іmax= 10 Вт/м2 (поріг больового відчуття). План Питання

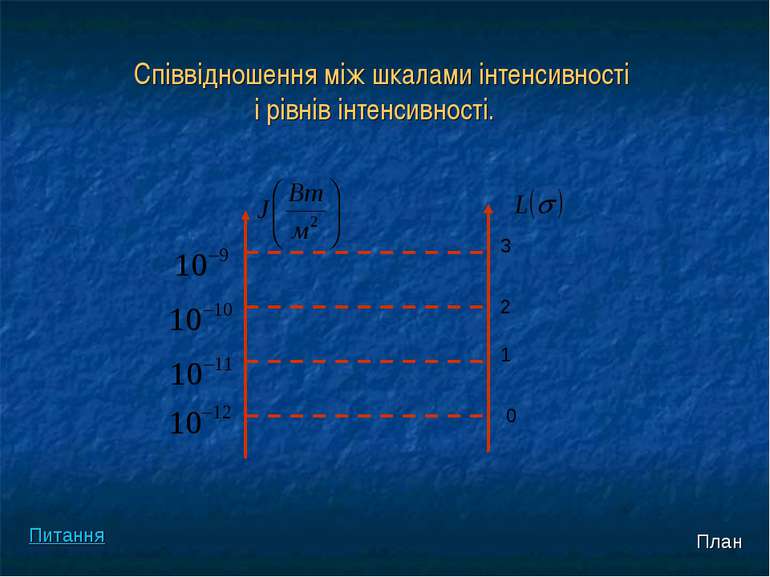
Для порівняння інтенсивності звуку користуються логарифмичною шкалою, тобто порівнюють їх логарифми. За нульовий рівень інтенсивності звуку приймають рівень інтенсивності звуку, що відповідає порогу чутності (Іо). Рівень інтенсивності звуку (L) визначається за формулою: Одиниця шкали рівнів інтенсивності 1 Бел (Б), який відповідає зміні інтенсивності звуку в 10 разів. План Питання

Співвідношення між шкалами інтенсивності і рівнів інтенсивності. 3 2 1 0 План Питання

Орган слуху: План Питання

Слуховий аналізатор. При виникненні в базилярній мембрані бігучої хвилі, в місцях максимального зміщення відбувається подразнення рецепторів. Локальне подразнення спричиняє виникнення серії електричих імпульсів у певному нервовому волокні, що входить до складу слухового нерву. По слуховому нерву в мозок передається серія імпульсів, що несуть інформацію про амплітуду та частоту коливань або інфомацію щодо спектрального складу звуку. Інформація піддається аналізу в слухових центрах кори головного мозку, де остаточно формується субєктивне віддчуття звуку. План Питання

Суб’єктивні (психофізичні) характеристики слухового відчуття:     гучність; висота тону; тембр. План Питання

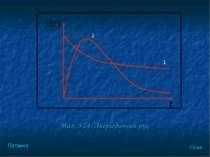
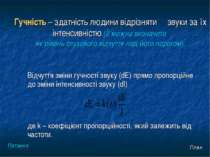
  Гучність – здатність людини відрізняти звуки за їх інтенсивністю.(Її можна визначити як рівень слухового відчуття над його порогом). Відчуття зміни гучності звуку (dЕ) прямо пропорційне до зміни інтенсивності звуку (dІ) де k – коефіцієнт пропорційності, який залежить від частоти. План Питання

Закон Вебер-Фехнера. Відчуття подразнення (Е) прямопропорційне логарифму сили самого подразнення (І). Іншими словами, якщо сила самого подразнення (І) зростає в геометричній прогресії (в 100, 1000, ... разів), то відчуття цього подразнення (Е) зростає в арифметичній прогресії (в 2, 3, ... рази) де k(v)=2.3(v)k План Питання

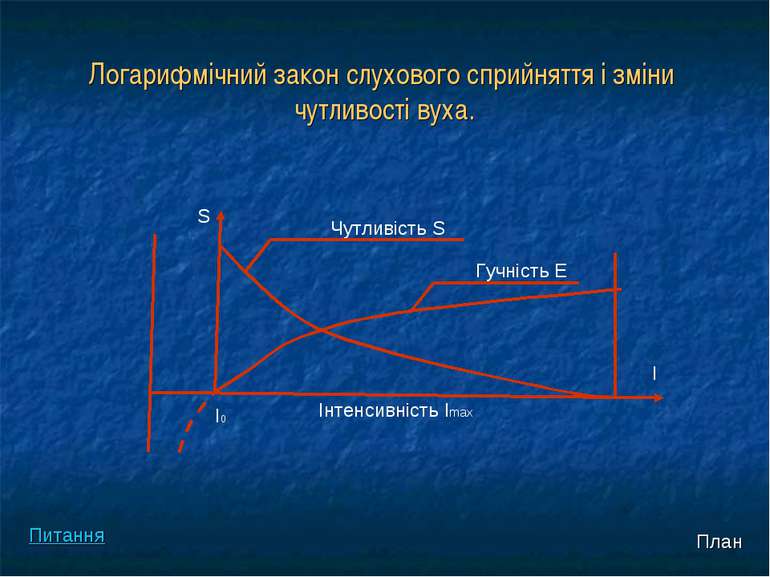
Логарифмічний закон слухового сприйняття і зміни чутливості вуха. Інтенсивність Іmax Чутливість S Гучність E S I0 I План Питання

  Висота – здатність людського вуха розрізняти тони за частотою: чим більша частота тону, тим вище звук. Одиниця висоти тону 1 мел. За 1000 мел приймають висоту тону звуку частотою 1000 Гц і інтенсивністю 60 дБ.   План Питання

Діапазон частот тонів, що сприймаються вухом, можна поділити на октави, для яких відношення частот крайніх гармонік дорівнює 2. Весь діапазон вміщує 10 октав. План Питання

Тембр – суб’єктивна оцінка “якості” звуку. Основою розрізнення звуків за тембром є здатність органів слуху розрізняти спектральний склад звуків. Існує таке правило:      - ноти звучать гармонійно (в унісон), якщо вони мають гармоніки однакової частоти; - ноти дисонують, якщо їх вищі гармоніки мають близькі частоти, але різниця цих частот надто велика для виникнення швидкого биття. План Питання

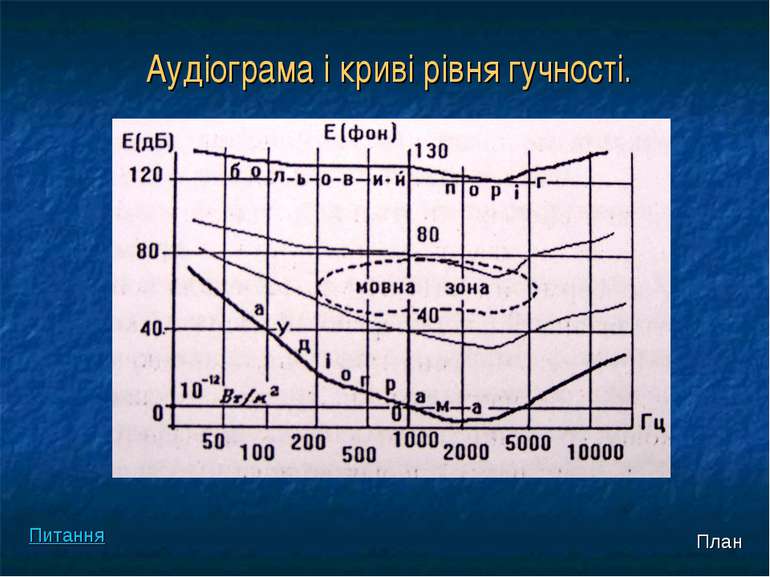
Запровадження шкали для оцінки суб’єктивного відчуття гучності звуку дозволяє вимірювати гучність звуку будь-якої частоти й інтенсивності, порівнюючи його зі звуком з частотою 1000 Гц. Крива нульового рівня гучності – аудіограма, яка є множиною значень інтенсивності звуку на порозі чутності для тонів різних частот у всьому діапазоні слухового сприйняття. План Питання

 Аудіограма і криві рівня гучності. План Питання

Методи вимірювання гостроти слуху мають назву аудіометрія. Аудіометр – спеціальний прилад, що являє собою генератор звуку з незалежним регулюванням частоти та інтенсивності. Методи клінічної аудіометрії дозволяють визначити послаблення слуху порівняно з нормою. Для цього визначають поріг чутності для різних тонів на аудіометрі. Будують аудіограму, яка свідчить про спектральну чутливість вуха людини на порозі чутності. Порівняння аудіограми хворої людини з нормальною дозволяє діагностувати захворювання органів слуху. План Питання

Ультразвукові коливання і хвилі – це такі пружні коливання і хвилі, які мають частоту в межах від 20 кГц до 109 Гц. Методи генерації та прийому ультразвукових коливань: механічний, в якому джерелом ультразвуку є енергія потоку газу чи рідини. (Недоліки методу: широкий спектр частот, нестабільність амплітуди); електромагнітний, в якому для отримання ультразвуку використовують енергію електричних коливань відповідної ультразвукової частоти.   План Питання

Властивості ультразвуку: будь-які зміни в середовищі, через яке проходить ультразвукова хвиля, приводить до зміни швидкості розповсюдження і поглинання цієї хвилі; відбиття хвилі від границі розподілу; акустична кавітація – поява мікропорожнин в матеріальному середовищі під дією коливань тиску. План Питання

Дія ультразвуку механічні ефекти (розрив, загибель бактерій); хімічні властивості (збудження та іонізація атомів і молекул з утворенням радикалів). План Питання

Застосування ультразвуку.   Застосування ультразвуку. План Питання

Інфразвукові коливання і хвилі – це пружні коливання з частотами до 16 Гц. Властивості : дуже слабо поглинається; розповсюджується майже без втрат на великі відстані. Для людини можуть бути шкідливими, оскільки деякі процеси в організмі людини відбуваються в інтервалі інфразвукових частот і дія інфразвукових хвиль може викликати шкідливі резонансні явища. План Питання

Питання: 1.     Що таке звук? 2.     Які розрізняються тони? 3.     Що таке інтенсивність звуку? 4.     Сформулюйте закон Вебера-Фехнера. 5.     Які ви знаєте об’єктивні характеристики звуку? 6.     Які ви знаєте суб’єктивні характеристики слухового відчуття? 7.     В чому суть методу клінічної аудіометрії? 8.     Як застосовується ультразвук в медицині? План

Практикум з біоренології стр. 237 - 258

.:: Лабораторна робота№1::. .::Лабораторна робота №2::. .::Лабораторна робота №3::.

Лабораторна робота №1 “Дослідження пружних властивостей біологічних тканин Мета: Одержати діаграму розтягу і стиснення та визначити основні показники пружних властивостей тканин (модуль Юнга, межу міцності, залишкову деформацію); Дослідити в’язко-пружні властивості біологічних тканин (текучість матеріалу); Контрольні питання

Додаткові теоретичні відомості Діаграма деформації Для ряду зразків( колаген, волосина, кістка, шкіра) при збільшенні деформацій їх жорсткість зменшується( див. мал. 3.34а); Для інших зразків (еластин, м’яз, стінка судини) жорсткість при розтязі різко збільшується до руйнування ( див. мал. 3.34б); Контрольні питання

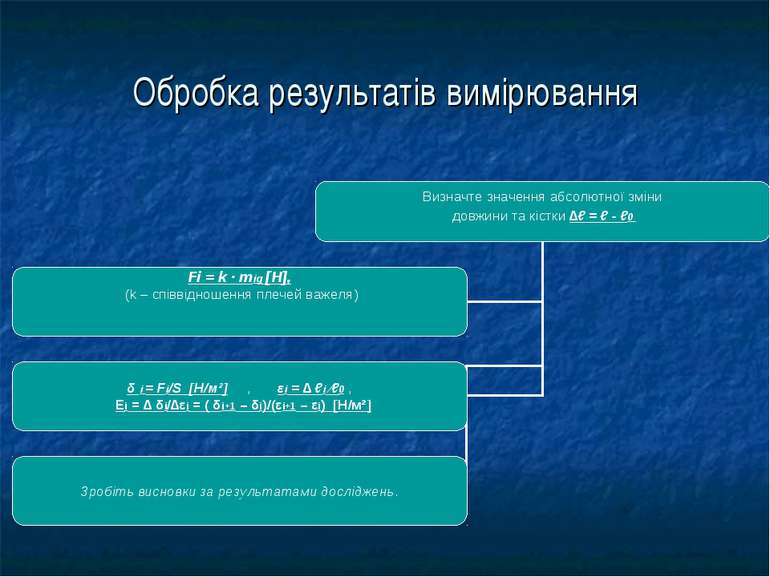
Для незначної лінійної деформації виконується закон Гука: δ = E ∙ ε В фізіологічному діапазоні зміни довжин користуються приведеним модулем Юнга (Eпр.): = Контрольні питання

Порядок виконання лабораторної роботи Зняття діаграми розтягу волосини. Ознайомтесь з макетом для розтягу волосини(мал.3.35); Підготуйте таблицю1; Мікрометром виміряйте діаметр волосини; Запишіть (ℓ0) волосини; Переміщуючи шток 5, збільшать прикладену силу F. Визначте (εзал) за положенням на шкалі 6; Дані заносьте в таблицю. Контрольні питання

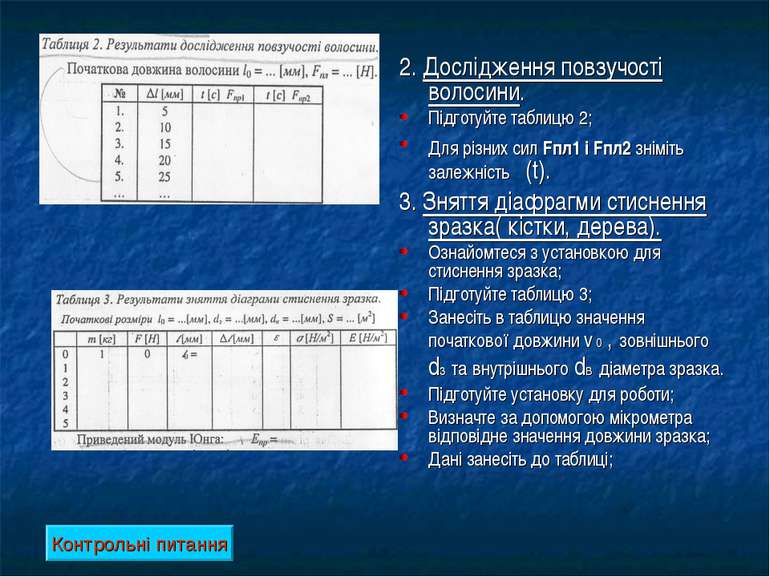
2. Дослідження повзучості волосини. Підготуйте таблицю 2; Для різних сил Fпл1 і Fпл2 зніміть залежність ε(t). 3. Зняття діафрагми стиснення зразка( кістки, дерева). Ознайомтеся з установкою для стиснення зразка; Підготуйте таблицю 3; Занесіть в таблицю значення початкової довжини ℓ0 , зовнішнього dз та внутрішнього dв діаметра зразка. Підготуйте установку для роботи; Визначте за допомогою мікрометра відповідне значення довжини зразка; Дані занесіть до таблиці; Контрольні питання

Обробка результатів вимірювання

Лабораторна робота №2 “Визначення коефіцієнта в’язкості ” Мета: Ознайомитися з методами визначення коефіцієнта в’язкості; Визначити коефіцієнт в’язкості розчину гліцерину; Контрольні питання

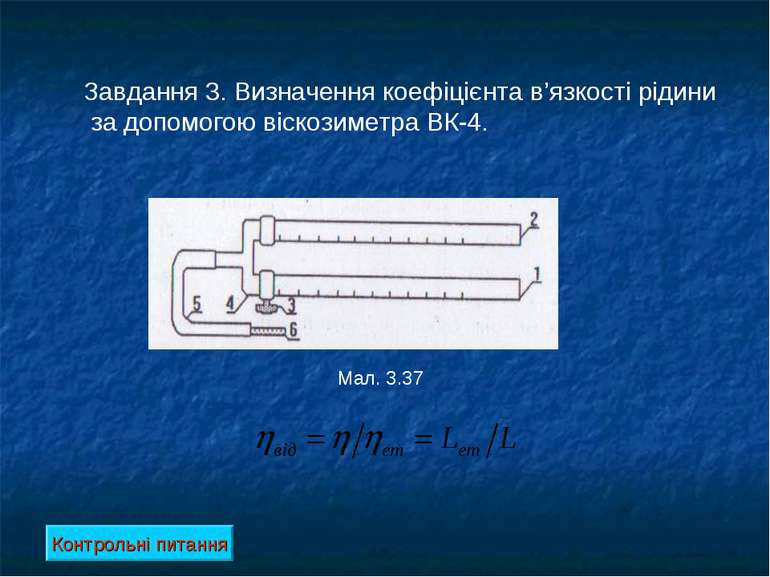
Додаткові теоретичні відомості Коефіцієнти в’язкості, значення яких лежать у межах 10 – 10 Па·с, визначаються за допомогою капілярних віскозиметрів. Капілярний метод базується на використанні формули Гагена-Пуазейля: За цими формула знаходять в’язкість рідини: [Па·с] Стала віскозиметра: Контрольні питання

Основні формули Контрольні питання

Порядок виконання лабораторної роботи Завдання 1. Ознайомитися з будовою капілярного віскозиметра. Контрольні питання

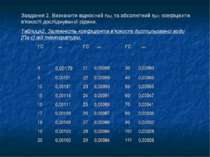
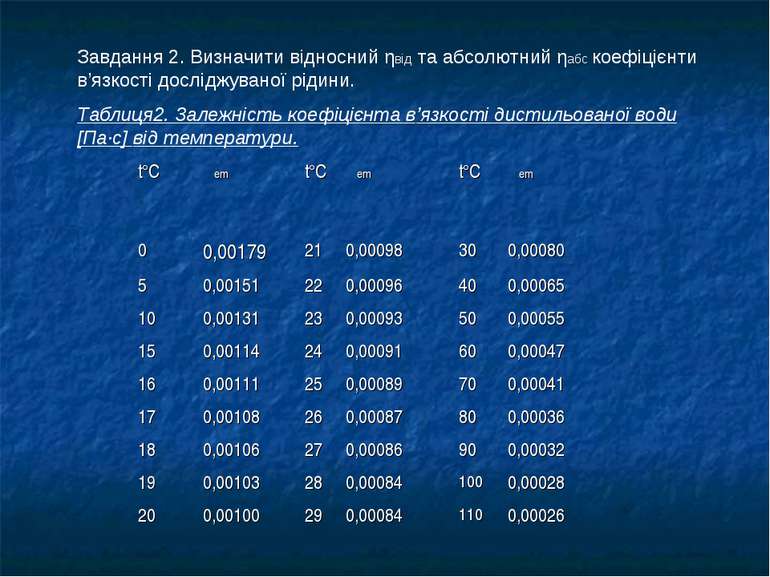
Завдання 2. Визначити відносний ηвід та абсолютний ηабс коефіцієнти в’язкості досліджуваної рідини. Таблиця2. Залежність коефіцієнта в’язкості дистильованої води [Па·с] від температури. t°C ηem t°C ηem t°C ηem 0 0,00179 21 0,00098 30 0,00080 5 0,00151 22 0,00096 40 0,00065 10 0,00131 23 0,00093 50 0,00055 15 0,00114 24 0,00091 60 0,00047 16 0,00111 25 0,00089 70 0,00041 17 0,00108 26 0,00087 80 0,00036 18 0,00106 27 0,00086 90 0,00032 19 0,00103 28 0,00084 100 0,00028 20 0,00100 29 0,00084 110 0,00026

Завдання 3. Визначення коефіцієнта в’язкості рідини за допомогою віскозиметра ВК-4. Мал. 3.37 Контрольні питання

Лабораторна робота №3 Мета роботи: Дослідити спектральну чутливість вуха на порозі чутності. Ознайомитись з роботою клінічного аудіометра. Контрольні питання

Додаткові теоретичні відомості Суб’єктивні. Характеристиками звуку є гучність звуку, висота, тембр. E = k · lg(I / I0) [дБ] Об’єктивні. Характеристиками звуку є інтенсивність або сила звуку, частота або частотний спектр. I = W / (S · t) , [Вт/м²] Контрольні питання

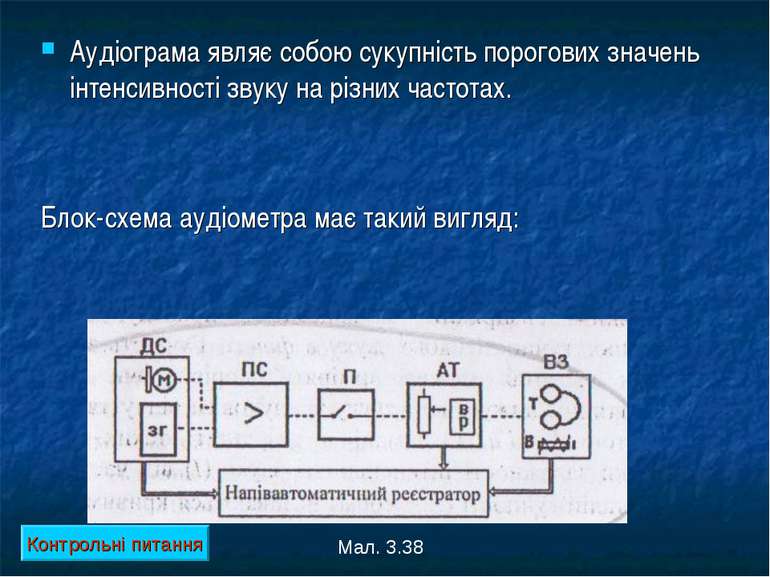
Аудіограма являє собою сукупність порогових значень інтенсивності звуку на різних частотах. Блок-схема аудіометра має такий вигляд: Мал. 3.38 Контрольні питання

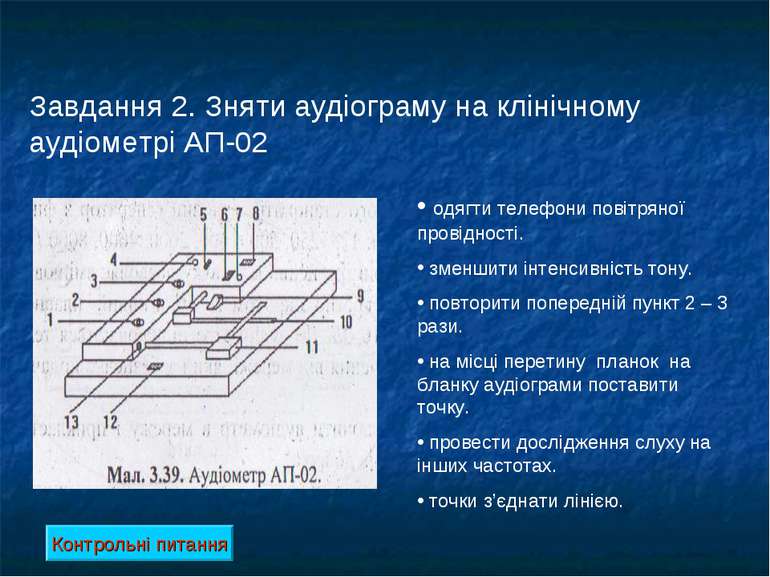
Завдання 2. Зняти аудіограму на клінічному аудіометрі АП-02 одягти телефони повітряної провідності. зменшити інтенсивність тону. повторити попередній пункт 2 – 3 рази. на місці перетину планок на бланку аудіограми поставити точку. провести дослідження слуху на інших частотах. точки з’єднати лінією. Контрольні питання

Дати якісне пояснення наведених нижче діаграм деформацій зразків: Чим відрізняються пружні властивості цих зразків? Чи змінюється модуль Юнга? Поясніть фізичний зміст модуля Юнга? Дайте визначення коефіцієнта в’язкості та вкажіть одиниці його виміру? Вкажіть об’єктивні та суб’єктивні характеристики звуку та відповідність між ними. Вкажіть одиниці їх вимірів. Що таке аудіограма? З яких основних частин складається аудіометр? Контрольні питання

Програмне забезпечення MS Word MS PowerPoint Adobe Photoshop Windows Media Player Easy CDDA Extractor Cool Edit Pro Mp3DirectCut