Презентація на тему:
Властивості квадратичної функції

Тема 3 Функція. Квадратична функція Поняття квадратичної функції. Графік функції y=x2+n. Графік функції y=(x+m)2 Графік функції y=(x+m)2+n. Графік функції y=ax2 Графік функції y=a(x+m)2+n Графік функції y=ax2+bx+c Властивості квадратичної функції Найпростіші перетворення графіків функцій Розв’язування вправ. Самостійна робота Розв'язування вправ

Пункт 4.1. Нулі функції Проміжки знакосталості функції Зростання і спадання функції Приклади дослідження функції Властивості квадратичної функції

Пункт 4.1. Нулі функції Парабола, яка є графіком квадратичної функції, може по різному розміщуватися відносно осі абсцис: 1) Перетинати її у двох точках; 2) Дотикатися до осі в одній точці; 3) Повністю знаходитися над віссю абсцис або під нею. Від чого залежить таке розміщення графіка? І висновок. Спрямування гілок параболи визначається знаком коефіцієнта а: Якщо а>0, то гілки параболи спрямовані вгору; Якщо а>0, то гілки параболи спрямовані вниз.

Пункт 4.1. Нулі функції Від чого залежить розміщення графіка? ІІ висновок В точці перетину графіка функції з віссю Ох значення цієї функції дорівнює нулю, робимо висновок, що кількість спільних точок параболи у = ах2 + bх + с й осі Ох дорівнює кількості коренів квадратного тричлена ах2 + bх + с, яка, у свою чергу, визначається значенням його дискримінанта: а) два різні корені (дві точки перетину), якщо D> 0; б) один корінь (одна спільна точка — точка дотику), якщо D = 0; в) жодного кореня (жодної спільної точки), якщо D< 0.

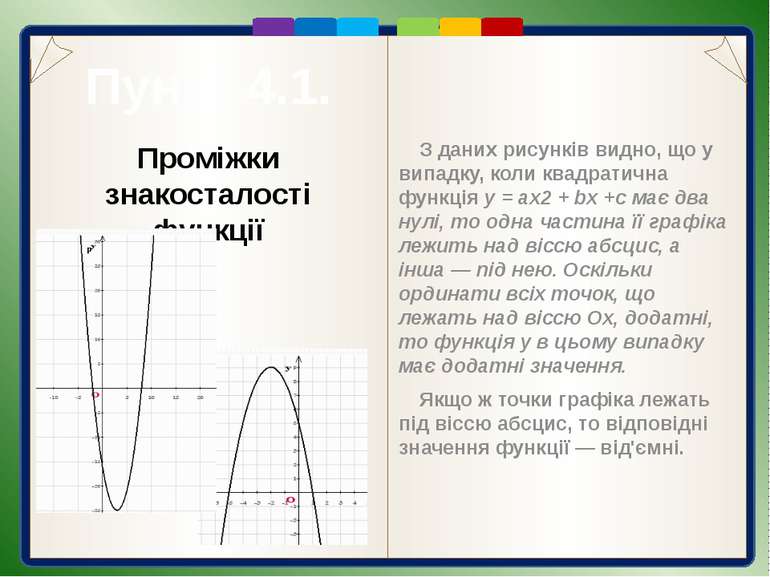
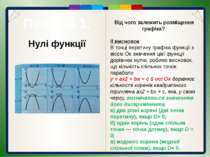
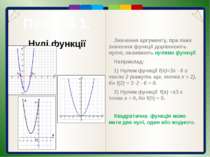
Пункт 4.1. Нулі функції Значення аргументу, при яких значення функції дорівнюють нулю, називають нулями функції. Наприклад: 1) Hулем функції f(x)=3x - 6 є число 2 (кажуть ще, точка x = 2), бо f(2) = 3 ·2 - 6 = 0. 2) Нулем функції f(х) =x3 є точка х = 0, бо f(0) = 0. Квадратична функція може мати два нулі, один або жодного.

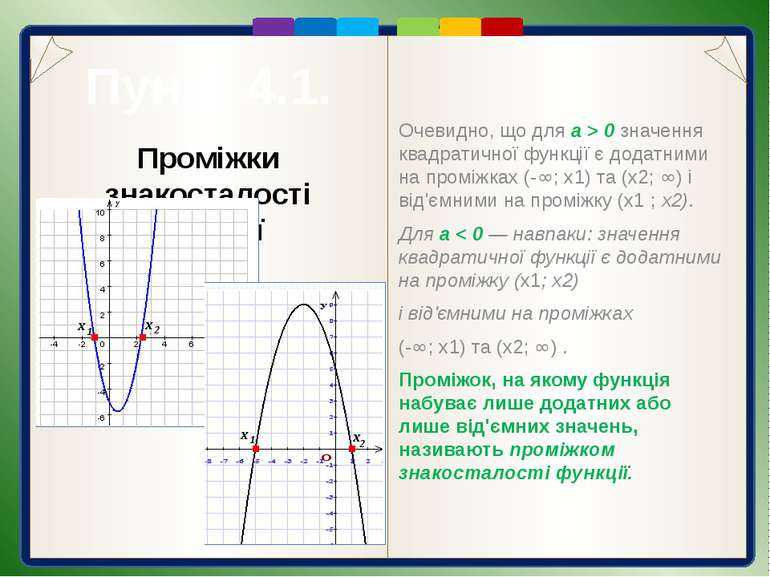
Пункт 4.1. Проміжки знакосталості функції З даних рисунків видно, що у випадку, коли квадратична функція у = ах2 + bх +с має два нулі, то одна частина її графіка лежить над віссю абсцис, а інша — під нею. Оскільки ординати всіх точок, що лежать над віссю Ох, додатні, то функція у в цьому випадку має додатні значення. Якщо ж точки графіка лежать під віссю абсцис, то відповідні значення функції — від'ємні.

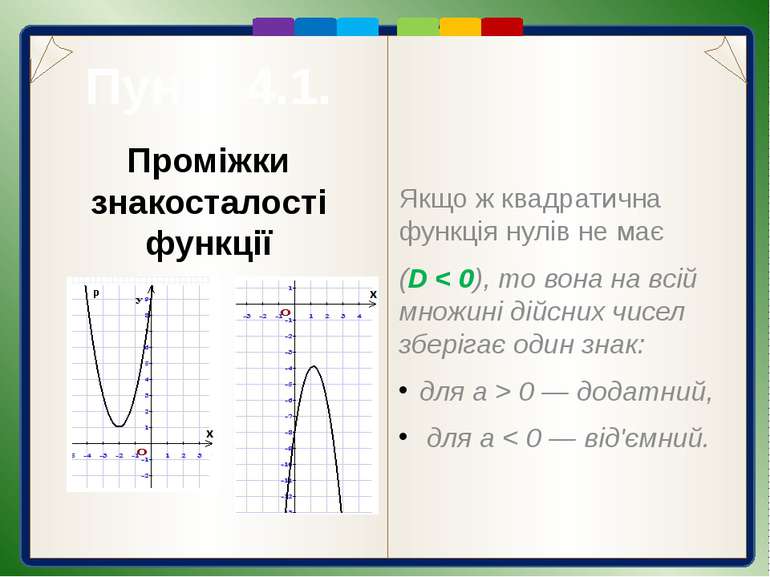
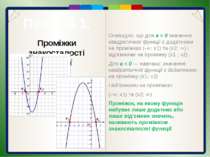
Пункт 4.1. Проміжки знакосталості функції Очевидно, що для а > 0 значення квадратичної функції є додатними на проміжках (-∞; х1) та (х2; ∞) і від'ємними на проміжку (х1 ; х2). Для а < 0 — навпаки: значення квадратичної функції є додатними на проміжку (х1; х2) і від'ємними на проміжках (-∞; х1) та (х2; ∞) . Проміжок, на якому функція набуває лише додатних або лише від'ємних значень, називають проміжком знакосталості функції.

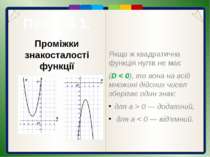
Пункт 4.1. Проміжки знакосталості функції Якщо ж квадратична функція нулів не має (D < 0), то вона на всій множині дійсних чисел зберігає один знак: для а > 0 — додатний, для а < 0 — від'ємний.

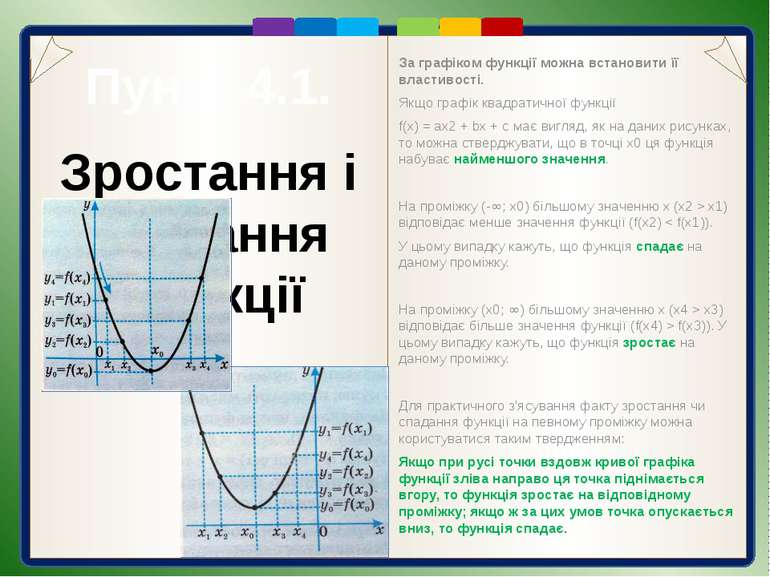
Пункт 4.1. Зростання і спадання функції За графіком функції можна встановити її властивості. Якщо графік квадратичної функції f(x) = ах2 + bх + с має вигляд, як на даних рисунках, то можна стверджувати, що в точці х0 ця функція набуває найменшого значення. На проміжку (-∞; х0) більшому значенню х (х2 > х1) відповідає менше значення функції (f(x2) < f(x1)). У цьому випадку кажуть, що функція спадає на даному проміжку. На проміжку (х0; ∞) більшому значенню х (х4 > х3) відповідає більше значення функції (f(x4) > f(x3)). У цьому випадку кажуть, що функція зростає на даному проміжку. Для практичного з'ясування факту зростання чи спадання функції на певному проміжку можна користуватися таким твердженням: Якщо при русі точки вздовж кривої графіка функції зліва направо ця точка піднімається вгору, то функція зростає на відповідному проміжку; якщо ж за цих умов точка опускається вниз, то функція спадає.

Пункт 4.1. Зростання і спадання функції Якщо графік квадратичної функції має вигляд, як на поданому рисунку, то, очевидно, в точці х0 ця функція набуває найбільшого значення. На проміжку (-∞; x0) вона зростає, а на проміжку (х0; ∞) — спадає. Точку, в якій відбувається перехід від зростання функції до спадання, або навпаки — від спадання до зростання (в розглянутому випадку — це точка x0 називають точкою екстремуму функції.

Пункт 4.1. Зростання і спадання функції Очевидно: якщо гілки параболи, яка є графіком квадратичної функції, спрямовані вгору, то в точці екстремуму функція набуває найменшого значення; Якщо гілки графіка квадратичної функції спрямовані вниз, то в точці екстремуму функція набуває найбільшого значення. Це значення дорівнює ординаті вершини параболи, яка є графіком даної квадратичної функції. Процес встановлення властивостей функції називають дослідженням функції.

Пункт 4.1. Приклади дослідження функцій Розв'язання. Оскільки а = 1,5 > 0, то гілки параболи, яка є графіком цієї функції, спрямовані вгору. Отже, в точці екстремуму функція набуває найменшого значення. Обчислимо його: Відповідь. У точці екстремуму функція набуває найменшого значення, яке дорівнює -5. Приклад 1. З'ясувати, якого значення (найбільшого чи найменшого) набуває функція у = 1,5х2 - 6х + 1 в точці екстремуму і обчислити це значення.

Пункт 4.1. Приклади дослідження функцій Розв'язання. Оскільки гілки параболи, що є графіком даної функції, спрямовані вниз (схематично його можна зобразити так, як на рис.), то на проміжку (-∞; х0), де х0 — абсциса вершини параболи, функція зростає, а на проміжку (х0; ∞) — спадає. Знайдемо х0 : Відповідь. Функція у = - х2 - 5х – 4 зростає на проміжку (-∞; -2,5) і спадає на проміжку (-2,5; ∞). Приклад 2. Вказати інтервали зростання і спадання функції у = - х2 - 5х – 4.

Приклади дослідження функцій Розв'язання. Позначимо одну зі сторін шуканого прямокутника через х. Тоді довжина другої сторони становитиме 8-х, а площа дорівнюватиме добутку х(8 - х). Математично задачу можна сформулювати так: при якому значенні х вираз х(8 - х), або функція у = х(8 - х), набуває найбільшого значення, враховуючи, що х>0 і 8-х>0 (як довжини сторін прямокутника)? Оскільки х(8 - х) = 8х-х2 =-х2+ 8х, то у = -х2 + 8х. Гілки параболи, що є графіком цієї функції, спрямовані вниз, тому найбільшого значення вона набуває в точці х, що є абсцисою вершини параболи. Знайдемо її. 8 — х = 8 — 4 = 4. Відповідь. Кожна зі сторін прямокутника дорівнює 4 см, тобто шуканий прямокутник є квадратом зі стороною завдовжки 4 см. Приклад 3. Якої довжини мають бути сторони прямокутника з периметром 16 см, щоб його площа була найбільшою? x см 8-x см S=x·(8-x)см2

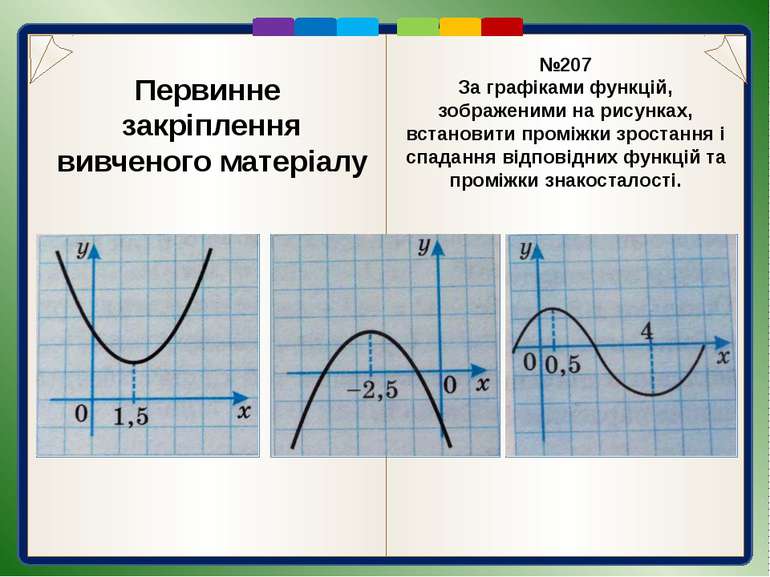
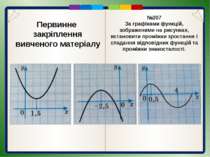
Первинне закріплення вивченого матеріалу №207 За графіками функцій, зображеними на рисунках, встановити проміжки зростання і спадання відповідних функцій та проміжки знакосталості.

Запитання для самоперевірки Що таке нулі функції? Скільки нулів може мати квадратична функція? Що називають проміжком знакосталості функції? За яких умов стверджують, що функція на даному проміжку: а) зростає б) спадає?

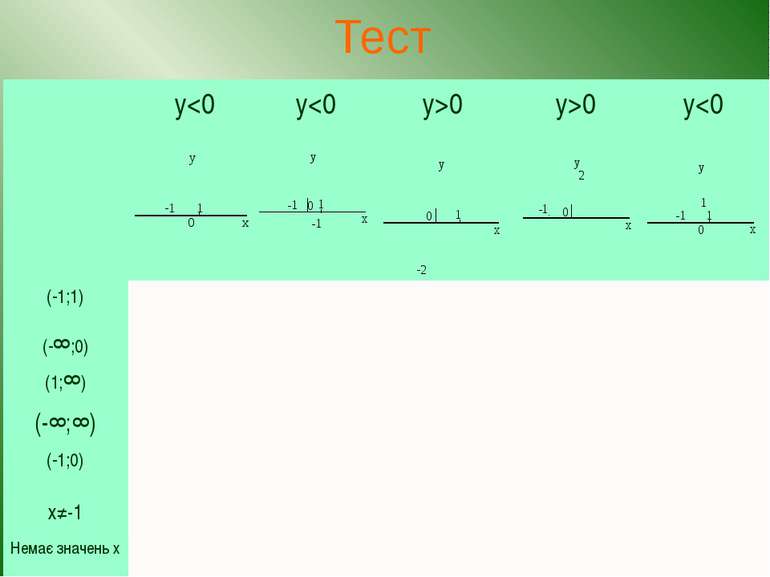
Тест Длякожноїізфункцій,графікиякихзображені,виберітьвідповіднуумовуівідмітьтезнаком «+». D>0;a>0 D>0;a

Тест (-1;1) (-∞;0) (1;∞) (-∞;∞) (-1;0) х≠-1 Немаєзначеньх у0 у