Презентація на тему:
Розв’язування прикладних задач

Розв’язування прикладних задач на знаходження найбільшого і найменшого значення функції на відрізку Презентацію підготувала учитель математики Жорова Л.А.

формування умінь і навичок розв’язування прикладних задач на знаходження найбільшого і найменшого значення функції на відрізку; розширення компетентностей учнів щодо застосування апарату диференціального обчислення до моделювання реальних життєвих процесів; розвиток логічного і творчого мислення, умінь аналізувати, робити висновки, використовувати отриману інформацію в особистому житті; виховування культури праці, інтересу до математики як засобу пізнання навколишнього світу

Вправа “Решето” Знайти похідну функції y= f(x). Знайти область визначення функції y= f(x) Упевнитися, що заданий відрізок входить до області визначення даної функції. Побудувати графік даної функції. Знайти критичні точки функції. Знайти проміжки зростання і спадання функції. Обчислити значення функції в критичних точках. Вибрати критичні точки, які належать заданому відрізку. Порівняти одержані значення функції та вибрати з них найменше і найбільше.

Задайте рівнянням функцію для розв’язання задачі Задача. (усно) Визначити розміри такого відкритого басейну з квадратним дном і об’ємом V=64м. куб., щоб на облицювання його дна і стін було витрачено найменшу кількість матеріалу.

Крок до майстерності Задача. Концентрація ліків у крові хворого через t секунд після ін’єкції задається формулою С(t)= Знайти максимальну концентрацію і час, коли вона досягається.

Готуємось до ЗНО Усна вправа Функція y=f(x) в точці x=5 має похідну, що дорівнює -1. Обчисліть значення похідної функції g(x)= f(x)x в точці x=5, якщо f(5)=3

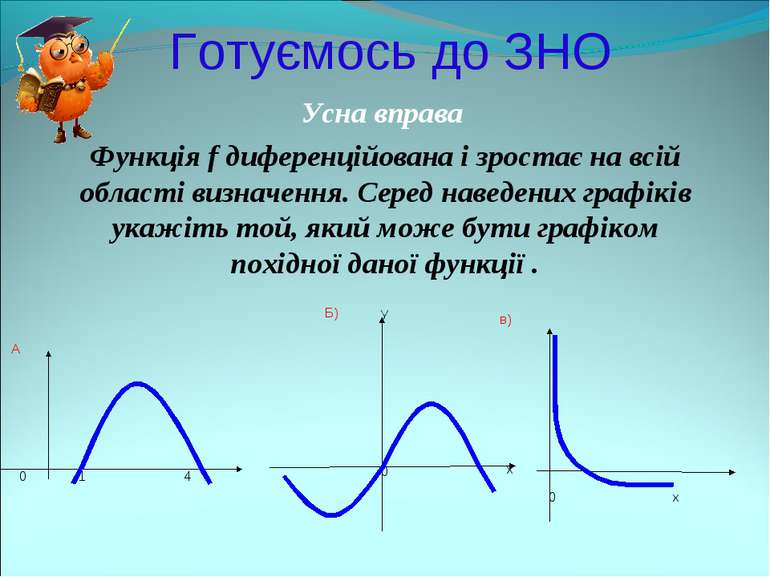
Готуємось до ЗНО Усна вправа Функція f диференційована і зростає на всій області визначення. Серед наведених графіків укажіть той, який може бути графіком похідної даної функції . x в) 0

Готуємось до ЗНО Обчисліть тангенс кута, який утворює з додатнім напрямом осі абсцис дотична до графіка функції y=cos2x у точці з абсцисою х= Усна вправа

Завдання додому Повторити пункт 5.3 за підручником Алгебра - 11 клас, академічний рівень, профільний рівень, автор Є.П. Нелін та ін. та пункти 3, 4 за підручником Алгебра - 10 клас, академічний рівень, автор А.Г. Мерзляк та ін. Виконати № 10 , 12, 14, с.91 за підручником Алгебра - 11 клас, академічний рівень, профільний рівень, автор Є.П. Нелін та ін.