Презентація на тему:
Застосування похідної до розв‘язування прикладних задач геометрії

Застосування похідної до розв‘язування прикладних задач

Розв'язання багатьох практичних задач зводяться до знаходження найбільшого та найменшого значень неперервної на відрізку функції, тобто знаходження екстремумів. Загальний метод розв'язування задач на екстремум за допомогою похідної складається з трьох етапів: формалізація (задача „перекладається" мовою функцій, для цього обирається зручний параметр х, через який шукану величину виражають як функцію f(x); розв'язання одержаної математичної задачі; інтерпретація знайденого розв'язку („переклад" його з мови математики у терміни первинної задачі).

Таблиця – схема плану дій

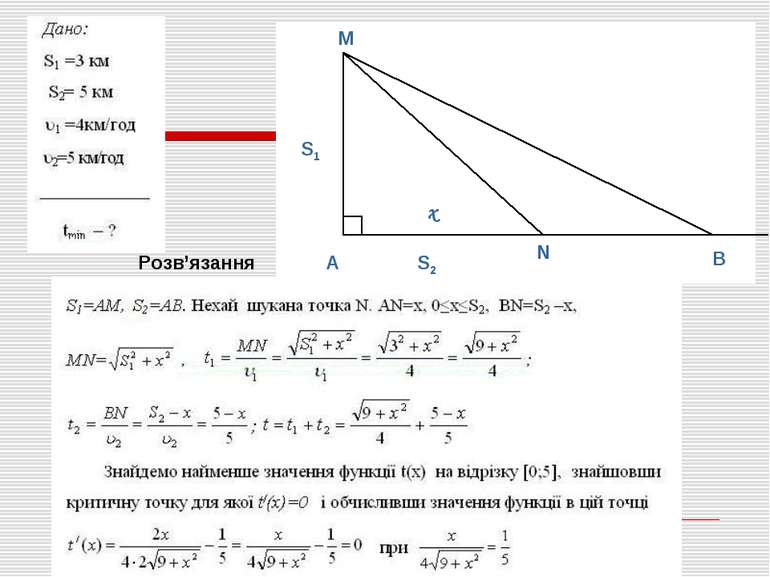
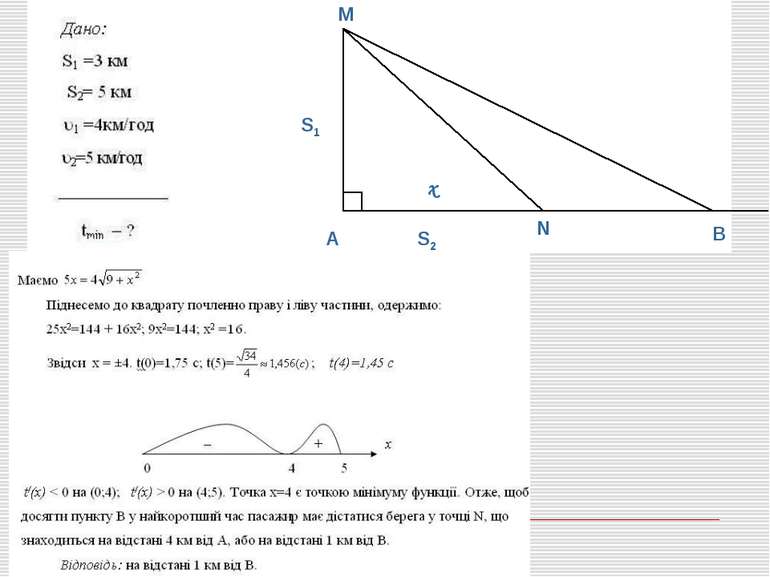
Задача 1 (№19 c.109) Човен знаходиться на озері на відстані 3 км від найближчої точки А берега. Пасажир човна має намір досягти села В, що розташоване на березі на відстані 5 км від А (ділянка AB берега вважається прямолінійною). Човен рухається зі швидкістю 4 км/год, а пасажир, вийшовши з човна, може за годину пройти 5 км. До якого пункту на березі має пристати човен, щоб пасажир прибув у село В за найкоротший час? М А В N x S1 S2

Розв’язання

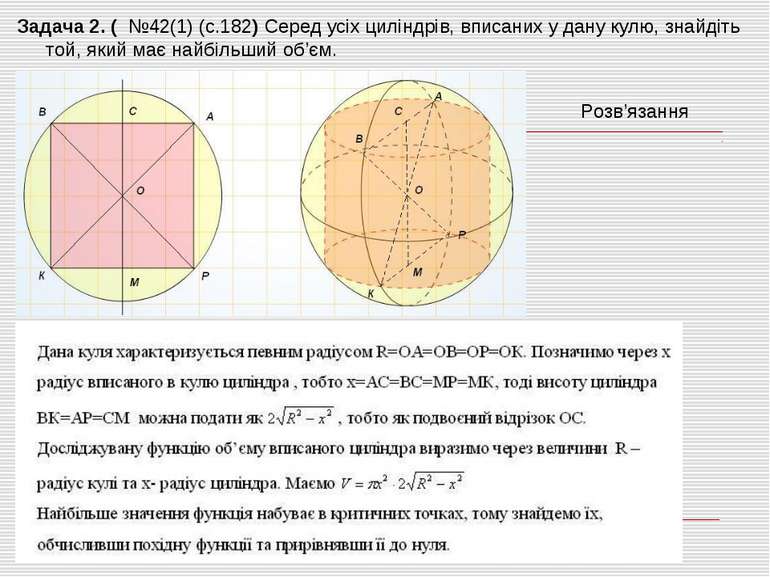
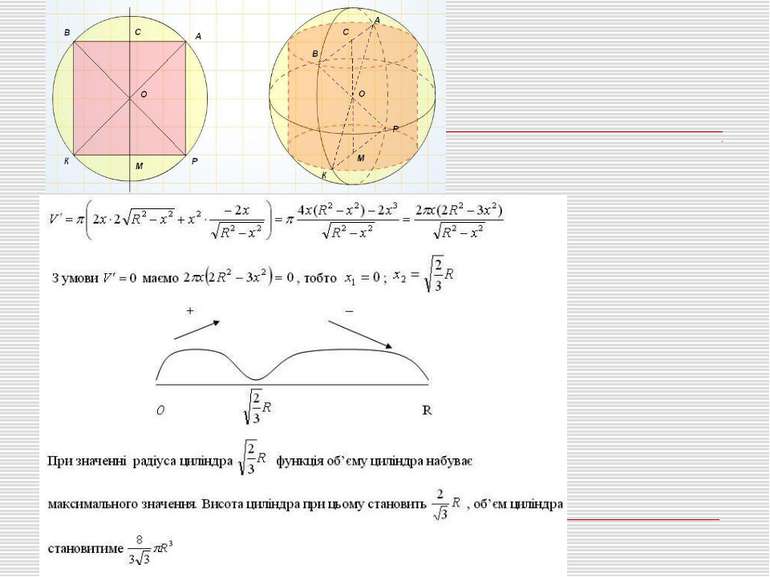
Задача 2. ( №42(1) (с.182) Серед усіх циліндрів, вписаних у дану кулю, знайдіть той, який має найбільший об’єм. Розв’язання

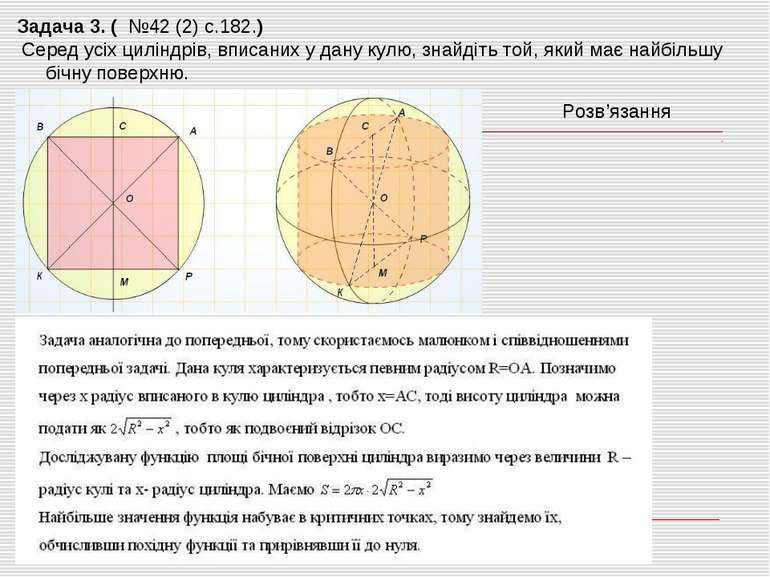
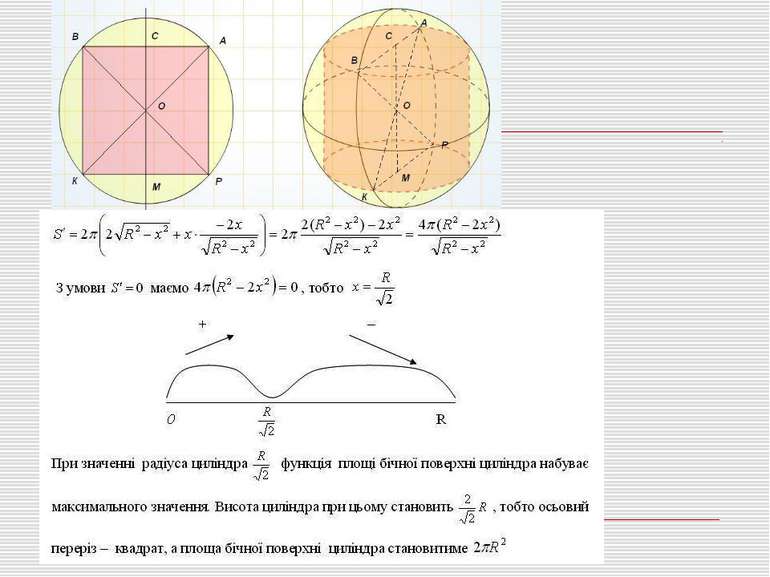
Задача 3. ( №42 (2) с.182.) Серед усіх циліндрів, вписаних у дану кулю, знайдіть той, який має найбільшу бічну поверхню. Розв’язання