Презентація на тему:
ПОНЯТТЯ ПРО ЗАСТОСУВАННЯ ІНТЕГРАЛА

ЗАСТОСУВАННЯ ІНТЕГРАЛА

Таблиця формул основних інтегралів

Площа  плоскої фігури. Обчислення площі в декартових координатах

Означення потрійного інтеграла: Нехай функція   визначена в замкненій обмеженій області   тривимірного простору  . Розіб’ємо область   на   довільних частинних областей  , які не мають спільних внутрішніх точок. Об’єми областей   позначимо позначимо   , їх діаметри -  . Діаметром   області  називається довжина найбільшої хорди, яка з’єднує дві точки межі області  . Візьмемо довільну точку  , і знайдемо значення функції   у точці  . Вираз вигляду   називається інтегральною сумою для функції   по області  . Позначимо через   максимальний із діаметрів   областей  , тобто  ,  . Якщо існує границя інтегральної суми  за умови, що  , тобто  , яка не залежить від способу розбиття області  а елементарні області   та від вибору точок  , то ця границя називається потрійним інтегралом від функції   по області  . Потрійний інтеграл позначається так: .

Обчислення площ у декартових координатах Як що плоска фігура (див. рис. 2.21) обмежена прямими лініями x = a, x = b  ( a 

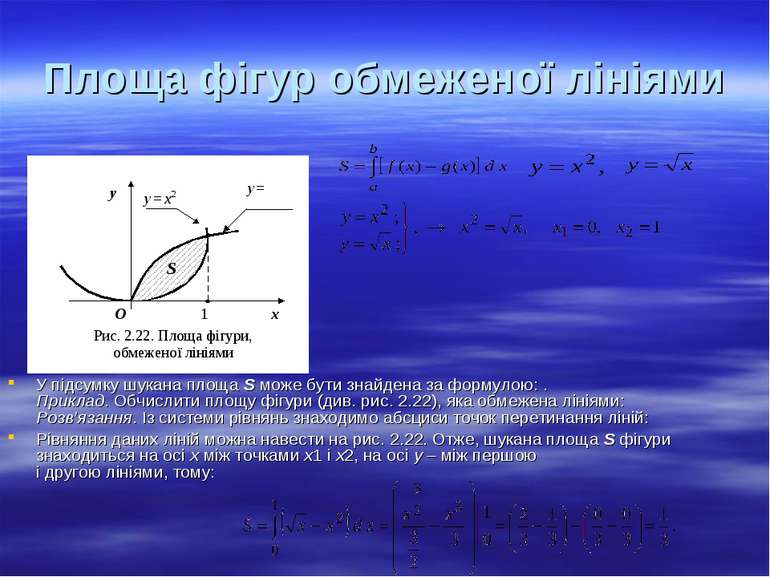
Площа фігур обмеженої лініями У підсумку шукана площа S може бути знайдена за формулою: . Приклад. Обчислити площу фігури (див. рис. 2.22), яка обмежена лініями: Розв’язання. Із системи рівнянь знаходимо абсциси точок перетинання ліній: Рівняння даних ліній можна навести на рис. 2.22. Отже, шукана площа S фігури знаходиться на осі х між точками х1 і х2, на осі y – між першою  і другою лініями, тому:

Властивості визначеного інтеграла

Застосування інтеграла I. У фізиці. Робота сили (>A=FScosa,cosa 1)Коли частку діє сила F, кінетична енергія іншого постійної. І тут відповідно до >d(mu2/2) =Fds прирощення кінетичною енергії частки під часdt односкалярному творуFds, деds – переміщення частки під часdt. Величина >dA=Fds називається роботою, чиненої силою F. Нехай точка рухається по осі ОХ під впливом сили, проекція чим вісь ОХ є функціяf(x) (>f–непреривная функція). Під впливом сили точка перемістилася з точкиS1(a) вS2(b).Разобьем відрізок [>a;b] на n відрізків, однаковою довжиниDx = (b –a)/n. Робота сили дорівнюватиме сумі робіт сили на отриманих відтинках.Т.к.f(x) –безупинна, то, при малому [>a;x1] робота сили у цьому відрізку дорівнюєf(a)(x1–a). Аналогічно другою відрізкуf(x1)(x2–x1), наn-ом відрізку —f(xn–1)(b–xn–1). Отже робота на [>a;b] дорівнює: А »An =f(a)Dx +>f(x1)Dx+...+f(xn–1)Dx= ((>b–a)/n)(f(a)+f(x1)+...+f(xn–1)) Приблизний рівність перетворюється на точне приn® b А =lim [(>b–a)/n] (f(a)+...+f(xn–1))=f(x)dx (з визначення) >n® a Приклад. Нехай пружина жорсткості З повагою та довжини l стиснута наполовину свій довжини. Визначити величину потенційної енергіїЕр дорівнює роботі A, чиненої силою –>F(s) пружність пружини при її стисканні, то >l/2 >Eп = A= – (–>F(s))dx 0 З курсу механіки відомо, щоF(s)= –>Cs. Звідси знаходимо >l/2l/2 >Еп= – (–>Cs)ds =CS2/2 | =C/2l2/4 0 0 Відповідь:Cl2/8. Координати центру мас Центр мас – точка якою проходить рівнодіюча сил тяжкості незалежно від просторовому розташуванні тіла. Нехай матеріальна однорідна пластина про має форму криволінійної трапеції {>x;y |>axb;0yf(x)} й третя функціяy=f(x) безупинна на [>a;b], а площаетойкриволинейной трапеції дорівнює P.S, тоді координати центру мас пластини про знаходять по формулам: b b>x0 = (>1/S) xf(x)dx;y0 = (>1/2S)f2(x)dx; a a Приклади. Центр мас. Знайти центр мас однорідної півкола радіуса R. >Изобразимполукруг у системі координатOXY. Із міркувань симетрії і однорідності помічаємо, що абсциса точки M >xm=0 Функція, яка описувалаполукруг має вигляд: y =(R2–x2) Нехай P.S =pR2/2 — площа півкола, тоді  R R y = (>1/2S)(R2–x2)dx = (>1/pR2)(R2–x2)dx = –R –R R = (>1/pR2)(R2x–x3/3)|=4R/3p R Відповідь:M(0;4R/3p ) Шлях, пройдений матеріальної точкою Якщо матеріальна точка рухається прямолінійно зі швидкістюu=u(t) і поза час T=t2–t1 (>t2>t1) пройшла цей шлях P.S, то >t2 >S=u(t)dt. >t1 У геометрії Обсяг — кількісна характеристика просторового тіла. За одиницю виміру обсягу приймають куб з руба1мм(1ди, 1 м тощо.). Кількість кубів одиничного обсягу розміщених у даному тілі — обсяг тіла. Аксіоми обсягу: Обсяг — ценеотрицательная величина. Обсяг тіла дорівнює сумі обсягів тіл, які його складають. Знайдемо формулу для обчислення обсягу: виберемо вісь ОХ в напрямі розташування цього тіла; визначимо кордону розташування тіла щодо ОХ;введемо допоміжну функціюS(x)задающую таке відповідність: кожному x з відрізка [>a;b] поставимо у відповідність площа перерізу даної постаті площиною, що проходить через задану точку x перпендикулярно осі ОХ. розіб'ємо відрізок [>a;b] на n рівних частин 17-ї та через кожну точку розбивки проведемо площину перпендикулярну осі ОХ, у своїй наше тіло розіб'ється на частини. По аксіомі >V=V1+V2+...+Vn=lim(S(x1)Dx +>S(x2)Dx+...+S(xn)Dx >n® >Dx®0, аSk®Sk+1, а обсяг частини, яка є між двома сусідніми площинами дорівнює обсягу циліндраVц=SоснH. Маємо суму творів значень функцій в точках розбивки на крок розбивки, тобто. інтегральну суму. За визначенням певного інтеграла, межа цієї суми приn® називається інтегралом a >S(x)dx B a V=S(x)dx, деS(x) – перетин площині, що проходить через b обрану точку перпендикулярно осі ОХ. Для перебування обсягу треба: 1). Вибрати зручним способом вісь ОХ. 2). Визначити кордону розташування цього тіла щодо осі. 3). Побудувати перетин даного тіла площиною перпендикулярно осі ОХ і що проходить через відповідну точку. 4). Висловити через відомі величини функцію, яка має площа даного перерізу. 5). Скласти інтеграл. 6).Вичислив інтеграл, знайти обсяг. Обсяг постатей обертання. Тіло, отриманий у результаті обертання пласкою постаті, щодо якийсь осі, називають постаттю обертання. ФункціяS(x) у постаті обертання є коло. >Sсеч =pr2 >Sсеч(x)=pf2(x) B V=f2(x) A Довжина дуги пласкою кривою Нехай на відрізку [>a;b] функція y =f(x) має безперервну похідну y’ =f ’(x). І тут довжину дуги l “шматка” графіка функції y =f(x),x[a;b] можна знайти за такою формулою B l =(1+f’(x)2)dx a

Виконав учень 11 класу Чемерис Павло