Презентація на тему:
Поняття про визначений інтеграл

Виконали: Крилова Д. Власова К. ТЗ-12 “б” ОНАХТ 2011

ПЛАН Задачі, що призводять до поняття визначеного інтегралу. Властивості в.і. Площа криволінійної трапеції. Наближене обчислення інтегралів. Формула Ньютона-Лейбниця. Методи інтегрального обчислення. Невласний інтеграл. Обчислення площин фігур. Довжина дуги. Об’єм тіла обертання.

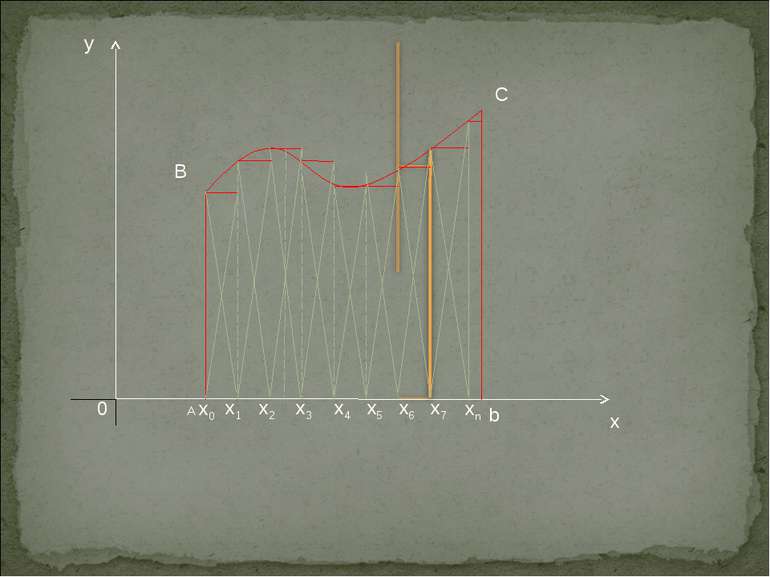
Задачі, що приводять до поняття визначеного інтегралу, можна звести до загального виду: Нехай задана функція f(x) на проміжку [a;b]. Поділимо на n-частин точками такими, що . Розглянемо довільний відрізок . На цьому відрізку виберемо . Розглянемо .Розглянемо Якщо є скінченим числом, то це число називається визначеним інтегралом від f(x) на [a;b], та позначається

Визначення Якщо існує кінцевий , не залежний від способа розбиття відрізка [a;b] на частини, та від вибору точок , то ця границя називається визначеним інтегралом функції f(x) на відрізку [a;b] і позначається

Теорема про існування визначеного інтегралу Якщо функція неперервна на проміжку , то існує і скінченна, тобто існує і скінчений

Властивості в.і. :

Властивості в.і. :

Зауваження. З геометричної точки зору за умови дорівнює площі криволінійної трапеції

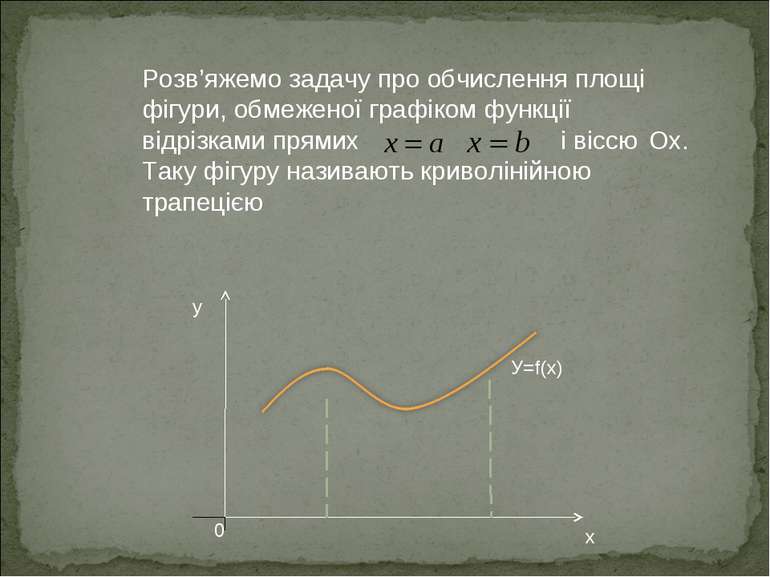
y Розв’яжемо задачу про обчислення площі фігури, обмеженої графіком функції відрізками прямих і віссю Ox. Таку фігуру називають криволінійною трапецією

Задача обчислення площі криволінійної трапеції.

y В С A b x0 xn

Задача про обчислення площі криволінійної трапеції.

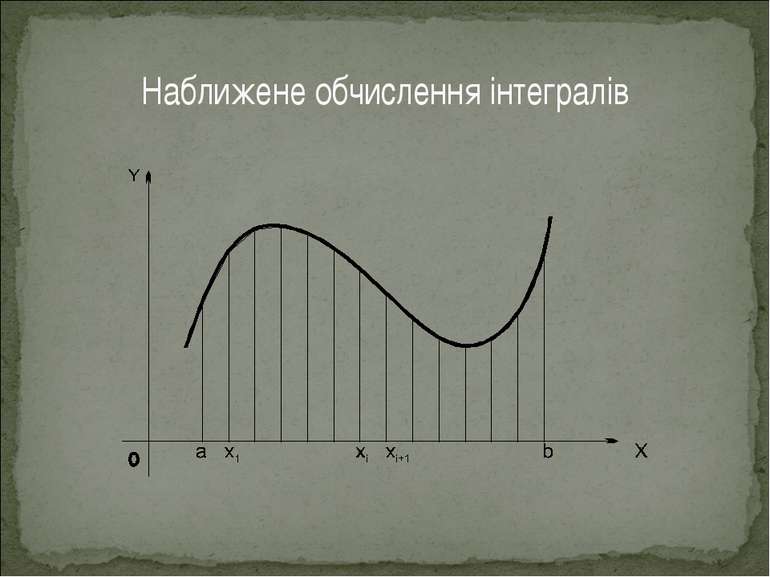
Наближене обчислення інтегралів Не всі інтеграли піддаються обчисленню. Виконується наближене обчислення визначених інтегралів, що не беруться через елементарні функції. Зокрема, виводяться формули наближеного обчислення прямокутників, формула трапецій, а також формула Сімпсона: де

Наближене обчислення інтегралів Тут шукана площа криволінійної фігури замінюється площею деякої ступенчатої фігури, яка складається із прямокутників. Ця наближена формула і називається формулою прямокутників. Зазвичай беруть якщо відповідну середню ординату позначити через то

Наближене обчислення інтегралів

Формула Ньютона-Лейбніца

Методи інтегрального обчислення

Методи інтегрального обчислення

Невласний інтеграл:

Обчислення площ

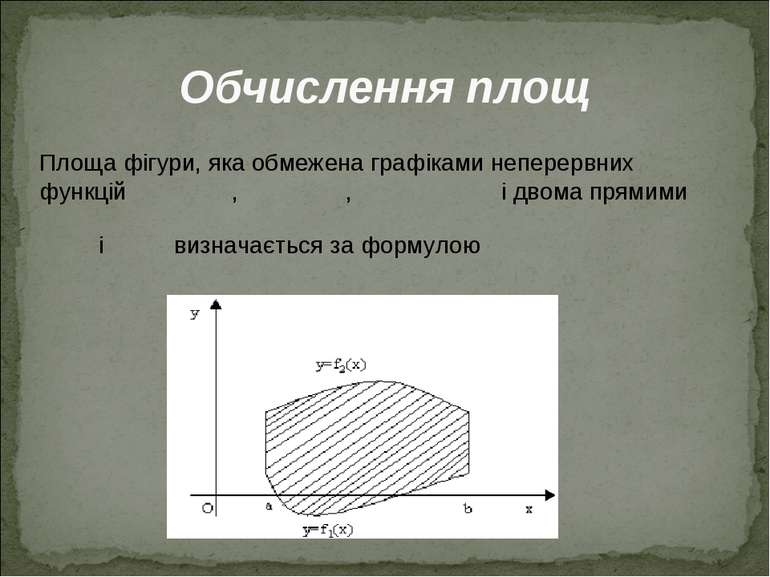
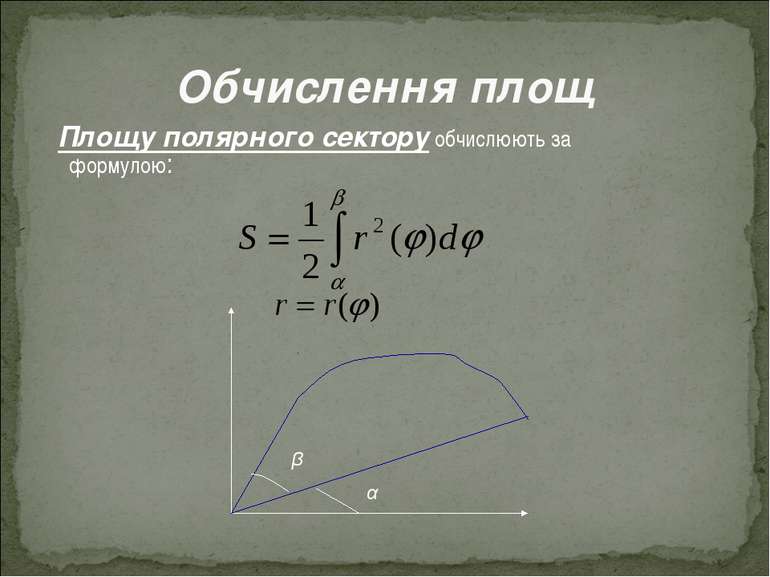
Обчислення площ У випадку параметричного завдання кривої, площу фігури, яка обмежена прямими , віссю Ох і кривою обчислюють за формулою де межі інтегрування визначають з рівнянь .

Площу полярного сектору обчислюють за формулою: β α Обчислення площ

Знайти площу еліпса . Параметричні рівняння еліпса у х Приклад обчислення площ

Якщо крива задана параметричними рівняннями , , то довжина її дуги , де – значення параметру, що відповідають кінцям дуги . Обчислення довжини дуги

Якщо крива задана рівнянням , то , де a, b–абсциси початку і кінця дуги . Якщо крива задана рівнянням , то , де c, d–координати початку і кінця дуги Довжина дуги в декартових координатах

Якщо крива задана рівнянням в полярних координатах , то , де –значення полярного кута, що відповідають кінцям дуги . Довжина дуги в полярних координатах

Нехай тіло утворюється при обертанні навколо осі OX криволінійної трапеції x1ABx2 Будь-який переріз цього тіла площиною, перпендикулярною до осі Ox буде круг, радіус якого дорівнює відповідній ординаті точки кривої Y=f(x) Площа перерізу S(x) рівна y2, т.е. S(x)= f2(x) Об'єм тіла обертання може бути вичислений по формулі Об'єм тіла обертання

ЗАДАЧА Обчислити об'єм кулі, що отримується обертанням півкола навколо осі OX Побудуємо півколо y X R -R R При обертанні цього півкола навколо OX виходить сфера, що обмежує кулю. Об'єм кулі знайдемо за формулою Відповідь: Об'єм кулі (куб.од.)