Презентація на тему:
Поняття про формули скороченого множення

Знання - це скарб, а розум – ключ до нього Вчитель математики Прохоренкова С. І.

Доброго дня! Сьогодні ми повторимо формули. Розглянемо способи доведення формул та наведемо приклади, а також вам будуть запропоновані завдання для самоперевірки. А тепер вперед. Бажаю успіху! Хлопчики та дівчатка! Я- ваш помічник, я проведу вас по темі : “ Формули скороченого множення ”

Історична сторінка Число – арифмос (греч.) Геометрія – гео – земля (греч.), метрео – міряю (греч.) Аль джебр – відновлення (арабск.)

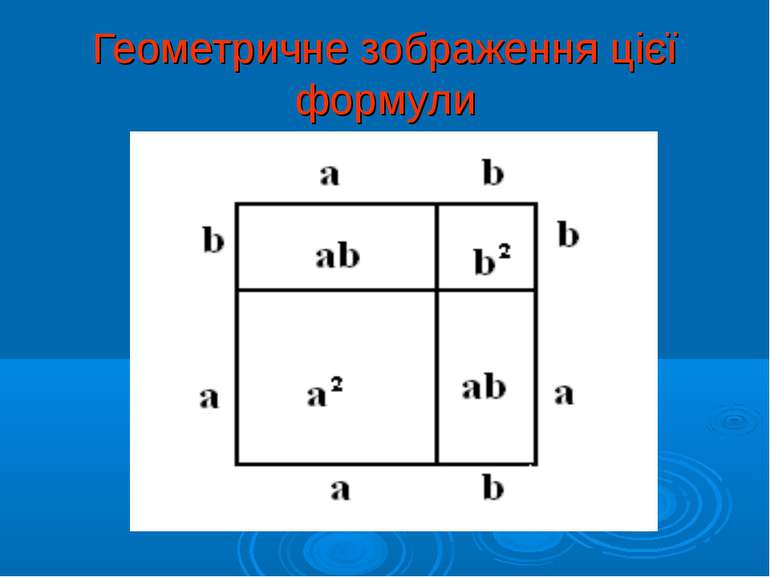
Евклід. “Начала” «Якщо відрізок яким-небудь чином розділити на два відрізки, то площа квадрата, побудованого на всьому відрізку, дорівнює сумі площ квадратів, побудованих на кожному з двох відрізків, та подвоєний площі прямокутника, сторонами якого є ці два відрізка.» Сенс цього виразу у формулі (а + b)2 = a2 + 2ab + b2

Геометричне зображення цієї формули

різниця квадратів двох виразів дорівнює добутку різниці цих виразів та їх суми a2-b2=(a+b)(a-b) Доведення: (a+b)(a-b)= a2-ab+ab-b2= a2-b2

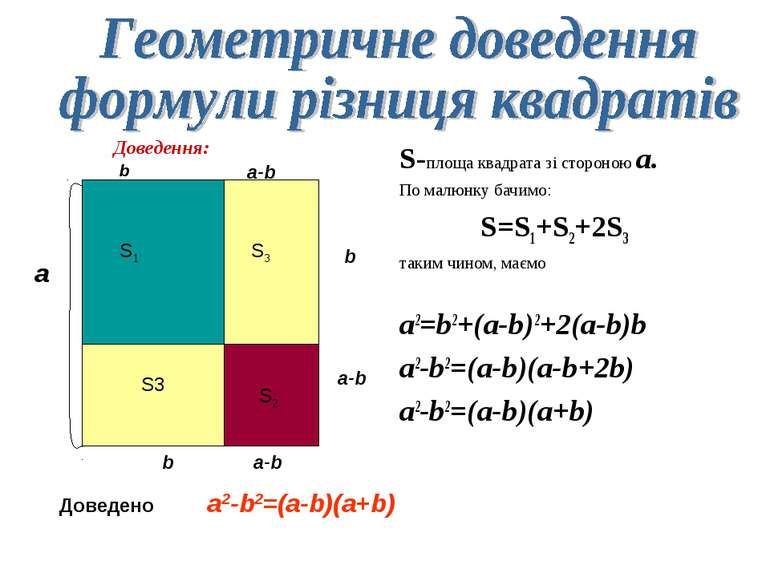
S-площа квадрата зі стороною a. По малюнку бачимо: S=S1+S2+2S3 таким чином, маємо a2=b2+(a-b)2+2(a-b)b a2-b2=(a-b)(a-b+2b) a2-b2=(a-b)(a+b) Доведення: Доведено a2-b2=(a-b)(a+b)

Ми розглянули два способи доведень формул. Бачите, що формулу можна доводити також і геометричним способом. Взагалі в математиці є три способи формулювання тверджень: Словесний – зрозумілий, але довгий, незручний; Геометричний – наглядний, але не завжди зручний для обчислень; Символьний – короткий, легко запам'ятовується. А зараз візьмемося до практичної роботи. Покажіть як застосовуються формула скороченого множення при розв'язуванні завдань .

Пригадаємо формули скороченого множення (а +b)2 = а2 + 2аb + b2 ; (а - b)2 = а2 – 2аb + b2 ; а3 – b3 = (а – b)(а2 + аb + b2); а3 + b3 = (а + b)(а2 -2аb + b2); а2 – b2 = (а + b)(а – b).

Складіть алгебраїчний вираз Сума квадратів чисел а та b. Різниця між числом m та подвоєної суми чисел а і b. Квадрат різниці чисел b та а. Різниця квадратів чисел а та b, помножена на суму цих чисел.

Заповніть пропуски (а +…)2 = … + 2аb + … ; (а … b)… = а2 – 2аb + … ; а3 - … = (а – b)(… + аb + …); а3 + b3 = (… …)(а2 … + b2); а2 – b2 = (… b)(а – …).

А зараз я пропоную вам познайомитись із задачею Піфагора.

«Будь-яке непарне число, крім одиниці, є різниця двох квадратів.» Розв'язування задачі: 1 спосіб: (n+1)2 - n2=(n+1-n)(n+1+n)=2n+1 – непарне число 2 спосіб. (n+1)2 - n2 = n2+2n+1-n2=2n+1 - непарне число В школі Піфагора ця задача розв'язувалась геометрично. Дійсно, якщо до квадрату зі стороною n додати гномом, що є непарним числом , 2n+1 (на мал. виділено червоним), то отримаємо квадрат зі стороною n+1, n2 +(2n+1)=(n+1)2 або (n+1)2 – n2=2n+1                                                                                                                                

Розв'яжи : Варіант 1 (3x+4)(3x-4)= (2-5n)(5n+2)= (7с2+4x)(4x-7c2)= 81p2-16a2= 25-36b4d2= 0,49a6-1= (8х + 3)2 = ( у – 4а )2 = Варіант 2 9x2-16 4-25n2 16x2-49c2 (9p+4a)(9p-4a) (5-6b2d)(5+6b2d) (0,7a3-1)(0,7a3+1) (10х – 7у)2 = ( 10 – с )2 =

Обчислюємо швидко А я здогадався, як можна використати формулу різницю квадратів для того, щоб швидко обчислювати. Дивись та вчись. 292-282=(29-28)(29+28)=1*57=57 732-632=(73+63)(73-63)=136*10=1360 1332-1342=(133-134)(133+134)= -267

(а + b + с)2 = а2 + b2 + с2 + 2аb + 2ас + 2bс Геометричне доведення “ЕРУДИТ”

Знайдіть квадрат виразу: а) (а – х + у)2 б) (а – b – с)2

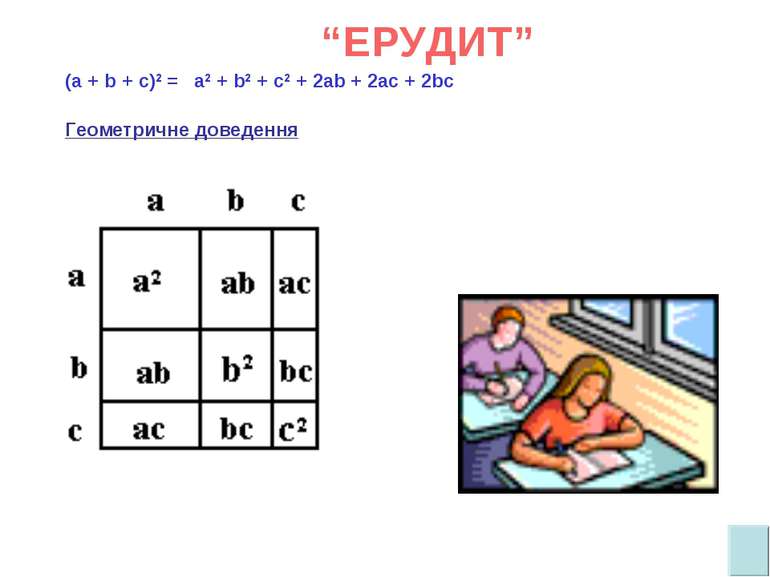
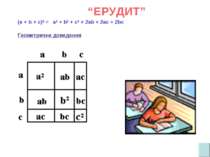
“ Ерудит ” Будь-яке натуральне число, яке закінчується цифрою 5, можна записати у вигляді 10а + 5. Наприклад, 25 = 2·10 + 5. Доведемо, для того, щоб обчислити квадрат такого числа можна до а(а + 1) дописати справа 25. Наприклад, 25² = 625, як 2 ·(2 + 1) = 6. Доведення: (10а + 5)² = 100a² + 100a + 25 = = 100a(a +1) + 25 = = a (a +1) ·100 + 25. За цим правилом знайдіть 45², 75², 115².

Приклади варіантів деяких формул: a2 + b2 = (a + b)2 – 2ab a2 + b2 = (a – b)2 + 2ab а2 = (a – b)(a + b) + b2

a2 = а2 – b2 + b2 = (a – b)(a + b) + b2, де b – доповнення числа а до круглого числа. Наприклад Обчислимо 9862 1. Кругле число 1000. а = 986, b = 14, а + b = 1000, a – b = 972. 2. 9862 = 972 1000 + 142 = 972000 + 196 = 972196.

ОБЧИСЛІТЬ САМОСТІЙНО 1) 1952 2) 4882

Математичний софізм Розглянемо дві різниці 16 – 36 та 25 – 45 Додамо число Маємо: 16 – 36 + = 25 – 45 + Запишемо ці вирази так: 42 – 2 * 4 * + = 52 – 2 * 5* + Використаємо формули: Отримаємо Доведемо, що 4=5

Ось і закінчився наш урок. На цьому уроці ви, діти, познайомились з формулами скороченого множення, розглянули способи їх доведення. Вам були запропоновані вправи і ви могли перевірити себе. Я тільки хочу вам нагадати, що при розв'язуванні завдань, задач, де є формули потрібно шукати різні способи, підходи. На все добре!