Презентація на тему:
Перетворення графіків тригонометричних функцій

Перетворення графіків тригонометричних функцій

Зміст Паралельне перенесення відносно осі OY Паралельне перенесення відносно осі ОХ Розтяг (стиск) в k раз відносно осі OY Розтяг (стиск) в k раз відносно осі OХ Симетричне відображення відносно осі OY Симетричне відображення відносно осі OX Побудова графіка y=|f(x)| Побудова графіка y=f(|x|)

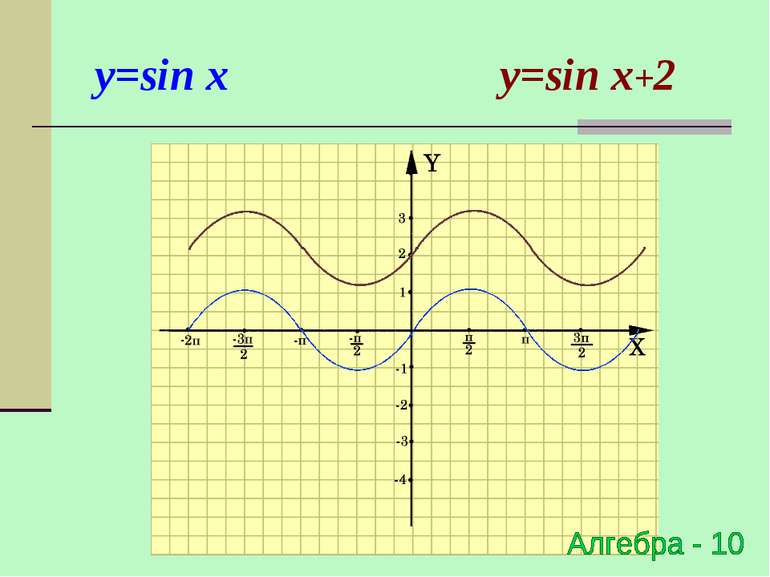
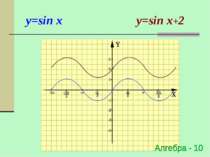
Паралельне перенесення відносно осі OY y=f(x) → y=f(x)+a (x0;y0) → (x0;y0+a) Для побудови графіка функції y=f(x)+a необхідно графік функції y=f(x) перенести відносно осі OY на вектор (0;а)

y=sin x y=sin x+2

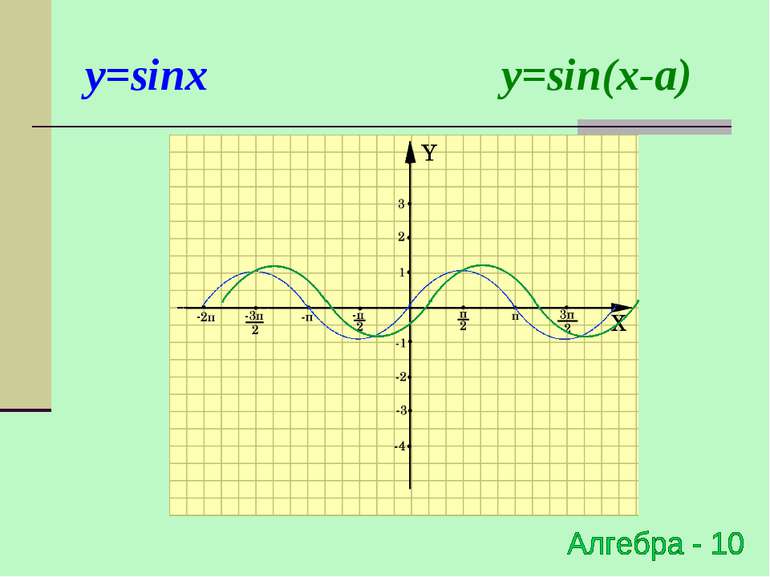
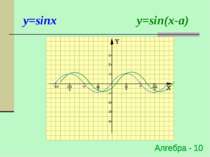
Паралельне перенесення відносно осі ОХ y=f(x) → y=f(x-a) (x0;y0) → (x0+a;y0) Для побудови графіка функції y=f(x-a) необхідно графік функції y=f(x) перенести відносно осі OX на вектор (0;а)

y=sinx y=sin(x-a)

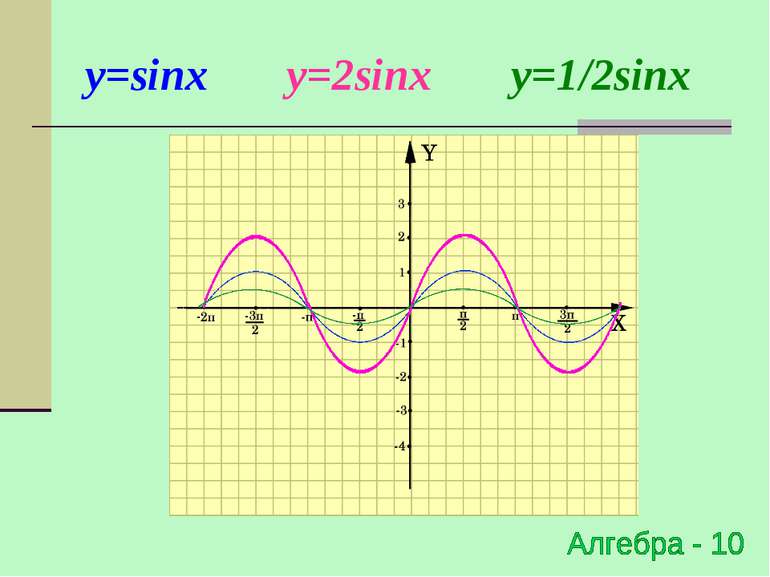
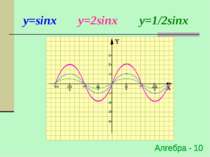
Розтяг (стиск) в k раз відносно осі OY y=f(x) → y=kf(x), де k>0 (x0;y0) → (x0;ky0) Для побудови графіка функції y=kf(x) необідно графік функції y=f(x) розтягнути в k раз відносно осі ОY для k >1 або стиснути в 1/k раз відносно осі OY для k

y=sinx y=2sinx y=1/2sinx

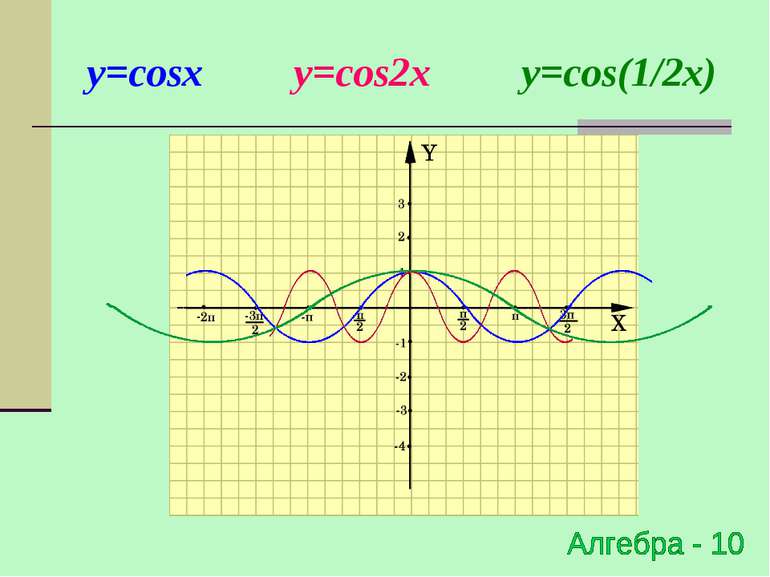
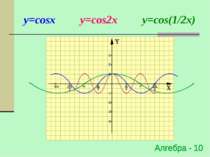
Розтяг (стиск) в k раз відносно осі OХ y=f(x) → y=f(kx), де k>0 (x0;y0) → ( x0;y0) Для побудови графіка функції y=f(kx) необхідно графік функції y=f(x) стиснути в k раз відносно осі ОХ для k >1 і розтягнути в 1/k раз відносно осі OХ для k

y=cosx y=cos2x y=cos(1/2x)

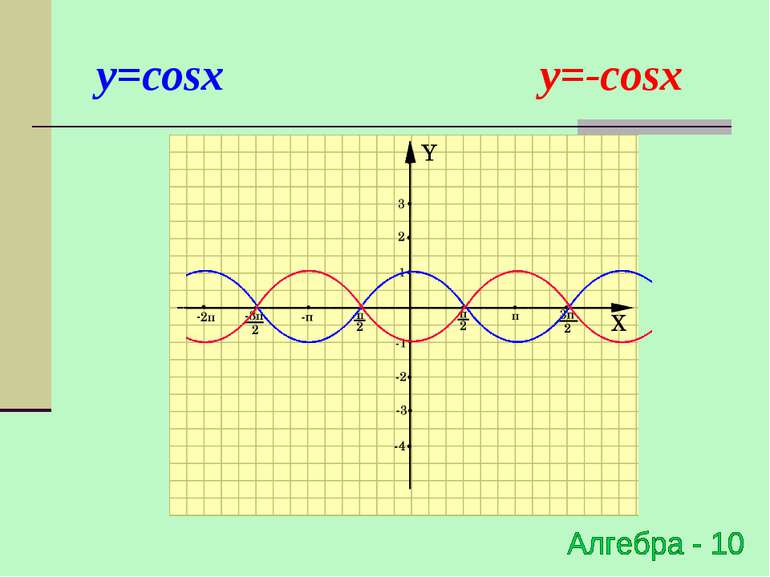
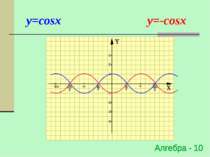
Симетричне відображення відносно осі OY y=f(x) → y=-f(x) (x0;y0) → (x0;-y0) Для побудови графіка функції y=-f(x) необхідно графік функції y=f(x) симетрично відобразити відносно осі ОХ

y=cosx y=-cosx

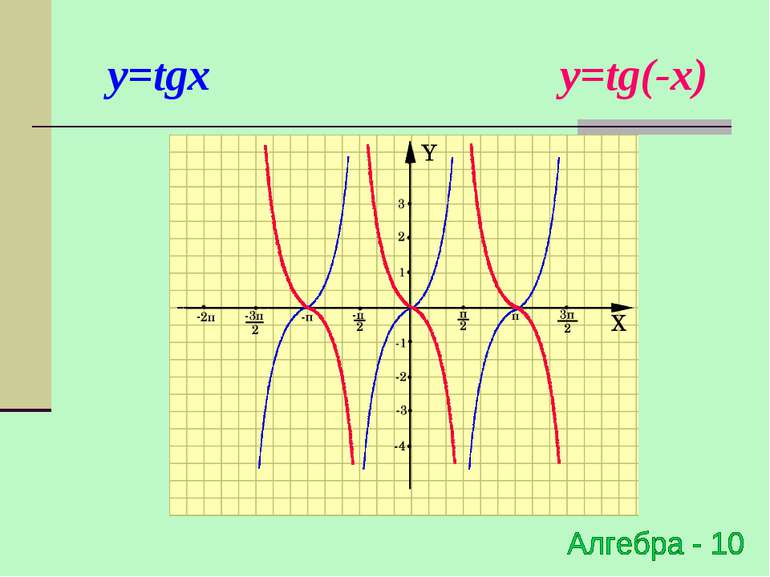
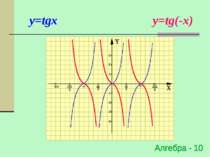
Симетричне відображення відносно осі OX y=f(x) → y=f(-x) (x0;y0) → (-x0;y0) Для побудови графіка функції y=f(-x) необхідно графік функції y=f(x) симетрично відобразити відносно осі ОY

y=tgx y=tg(-x)

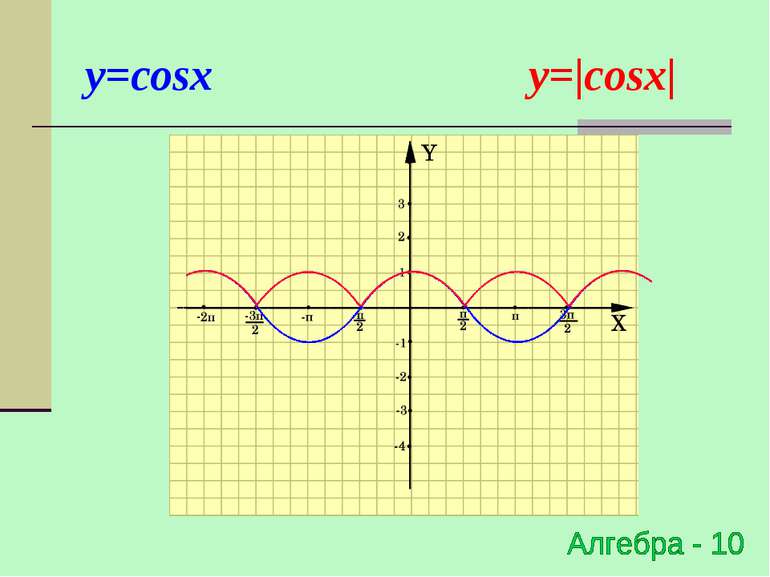
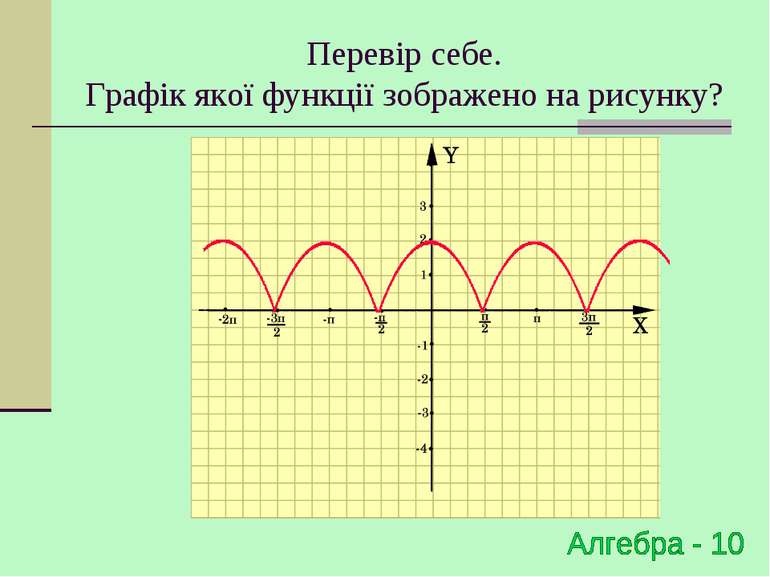
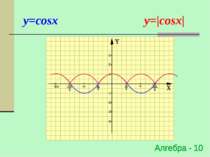
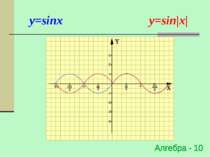
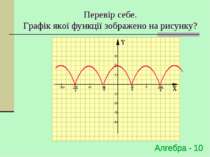
Побудова графіка y=|f(x)| Для побудови графіка функції y=|f(x)| необхідно частину графіка функції y=f(x), що знаходиться вище осі OX - залишити незмінною, а частину графіку y=f(x), що знаходиться нижче осі OХ - симетрично відобразити відносно осі ОХ f(x), якщо х 0 y=|f(x)|= -f(x), якщо х < 0

y=cosx y=|cosx|

Побудова графіка y=f(|x|) f (x), якщо х 0 y=f (|x|)= f (-x), якщо х

y=sinx y=sin|x|

Перевір себе. Графік якої функції зображено на рисунку?