Презентація на тему:
Обернена тригонометрична функція y=arcsin x

Підготували: Бушина Інна Борисівна, вчитель математики та інформатики ЗОШ № 5 м. Черкаси, вища категорія, вчитель-методист; Павліченко Світлана Петрівна, вчитель математики ЗОШ № 10 м. Черкаси , друга категорія

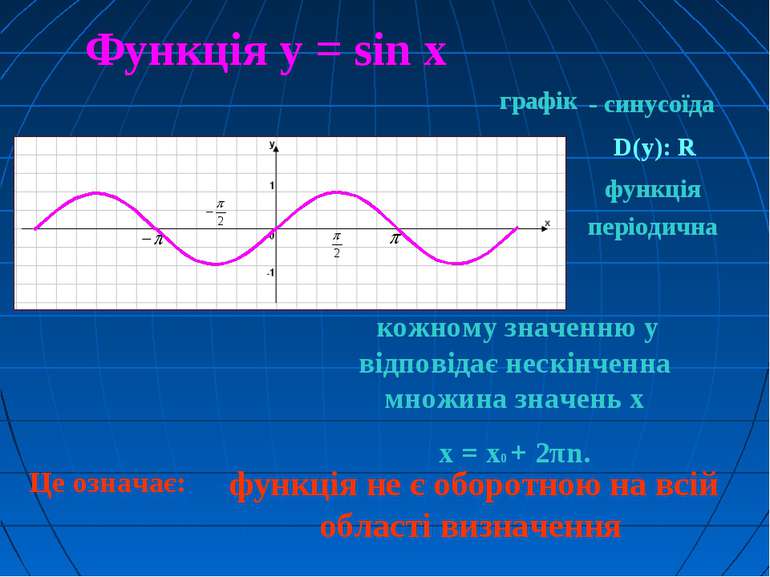
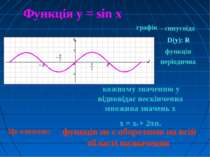
Це означає: Функція у = sin x кожному значенню у відповідає нескінченна множина значень х х = х0 + 2πn. графік - синусоїда функція не є оборотною на всій області визначення D(у): R функція періодична

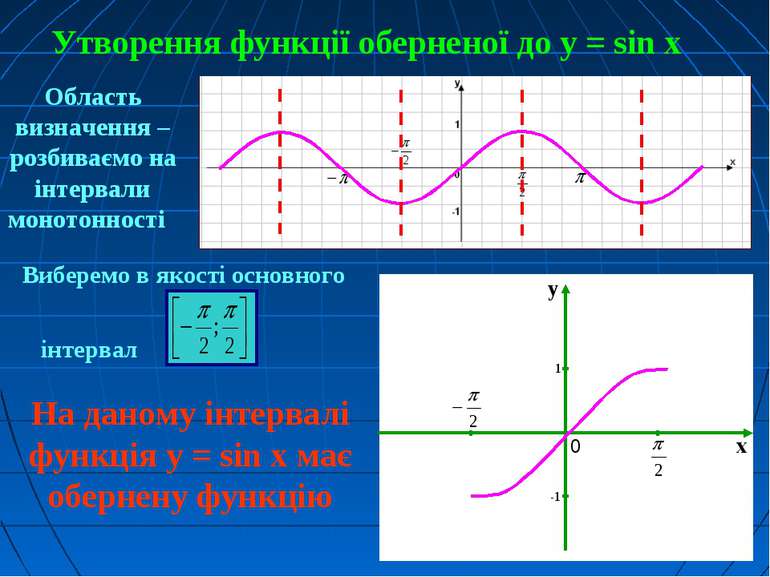
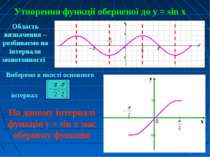
Утворення функції оберненої до у = sin x Виберемо в якості основного інтервал Область визначення – розбиваємо на інтервали монотонності На даному інтервалі функція у = sin x має обернену функцію                                                                                                                                                                                                                

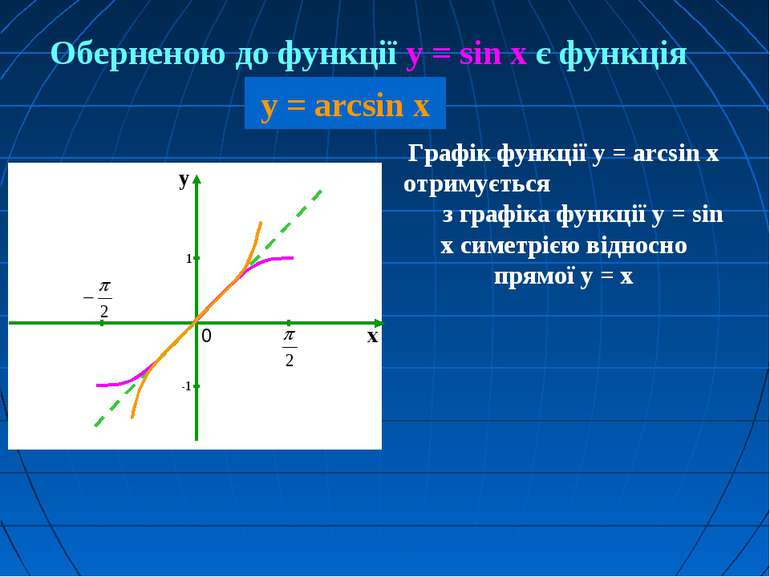
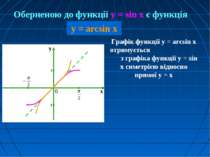
Графік функції у = arcsin x отримується з графіка функції у = sin x симетрією відносно прямої у = х Оберненою до функції y = sin x є функція у = arcsin x                                                                                                                                                                                                                

1. Область визначення у = sin x у = arcsin x [-1 ; 1] 2. Область значень 1 - 1 [-1 ; 1] 3. Функція непарна 4. Неперіодична 5. Нулі функції O(0;0) 6. Функція зростаюча 7. y > 0 при х є [0;1] y < 0 при х є [-1;0]                                                                                                                                                                                                                

arcsin x називається таке число з проміжку , y = arcsin x синус якого дорівнює х. Означення

1. Для яких значень змінної х визначений вираз arcsin х ? А) 0 < х < 1. Б) -1 ≤ х ≤ 1. В) - ∞ < х < ∞ . Г) -1 < х < 1. 2. Для яких значень змінної х визначений вираз arcsin (х – 2) ? А) -1 ≤ х ≤ -1. Б) - ∞ < х < ∞ . В) 1 ≤ х ≤ 3. Г) -3 ≤ х ≤ -1. Перевір себе

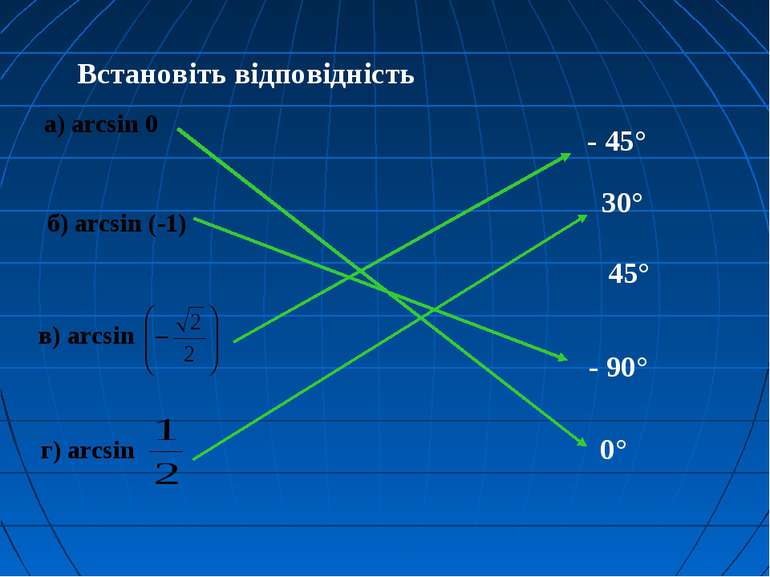
Встановіть відповідність а) arcsin 0 в) arcsin г) arcsin - 45° 45° 30° 0° - 90° б) arcsin (-1)

3. У якій чверті лежить кожен із кутів: 1) arcsin 0,7 2) arcsin (-0,35) А) І. Б) ІІ. Г) ІV. В) ІІІ. 4. Обчисліть : 1) arcsin 2) arcsin + arcsin А) . Б) 2π . В) . Г) π .

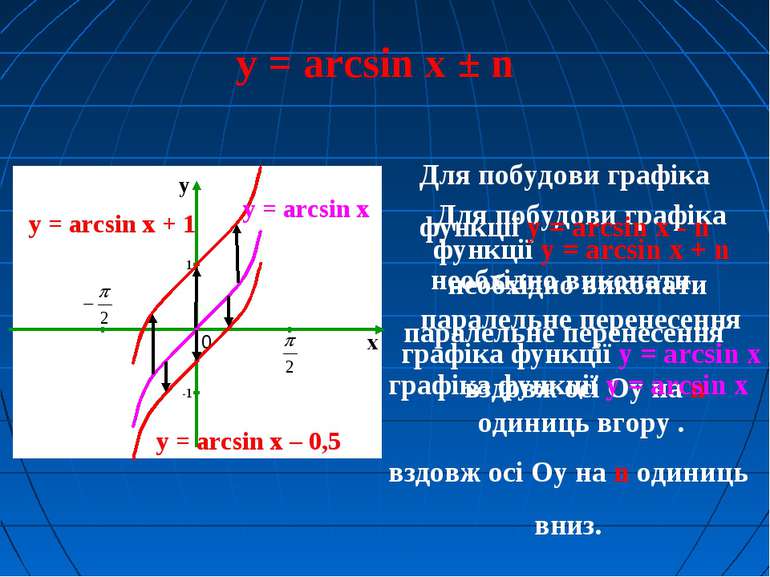
y = arcsin x ± n y = arcsin x Для побудови графіка функції y = arcsin x + n необхідно виконати паралельне перенесення графіка функції y = arcsin x вздовж осі Oy на n одиниць вгору . y = arcsin x + 1 Для побудови графіка функції y = arcsin x - n необхідно виконати паралельне перенесення графіка функції y = arcsin x вздовж осі Oy на n одиниць вниз. y = arcsin x – 0,5                                                                                                                                                                                                                

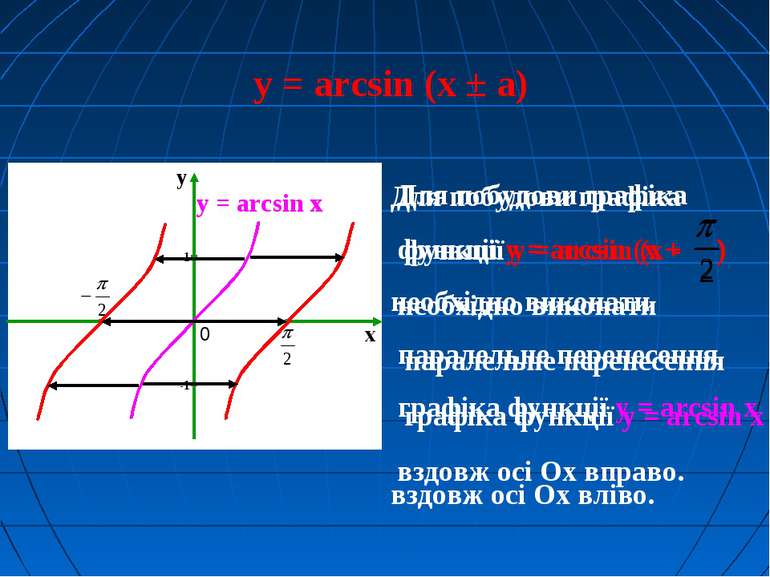
y = arcsin (x ± а) Для побудови графіка функції y = arcsin (x + ) необхідно виконати паралельне перенесення графіка функції y = arcsin x вздовж осі Oх вліво. y = arcsin x Для побудови графіка функції y = arcsin (x - ) необхідно виконати паралельне перенесення графіка функції y = arcsin x вздовж осі Oх вправо.                                                                                                                                                                                                                

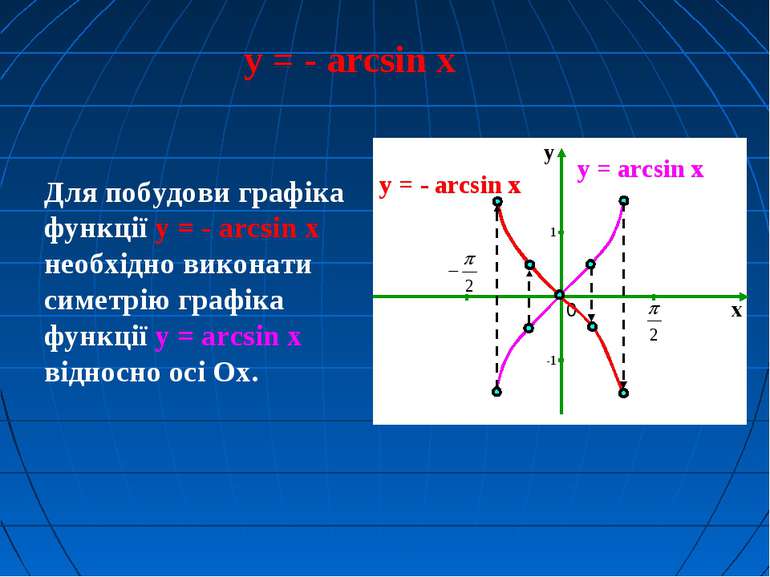
y = - arcsin x Для побудови графіка функції y = - arcsin x необхідно виконати симетрію графіка функції y = arcsin x відносно осі Ox. y = arcsin x y = - arcsin x                                                                                                                                                                                                                

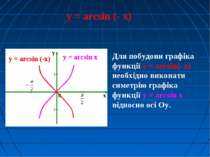
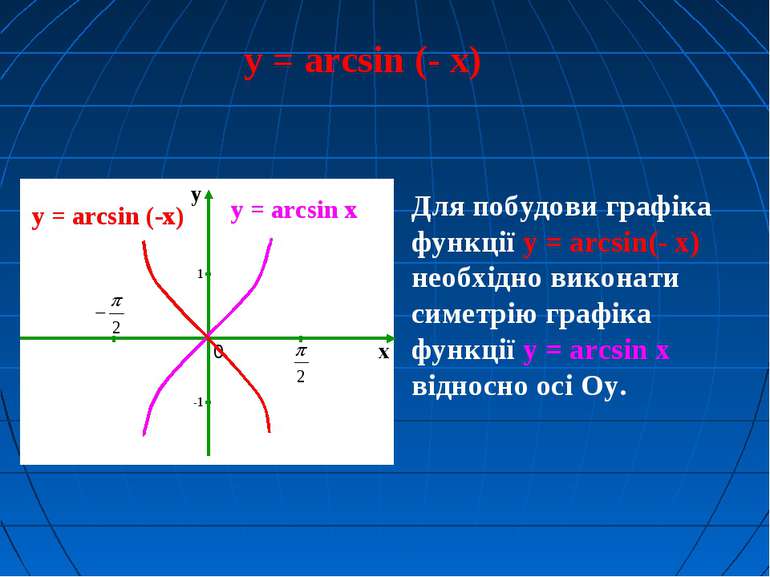
y = arcsin (- x) y = arcsin x Для побудови графіка функції y = arcsin(- x) необхідно виконати симетрію графіка функції y = arcsin x відносно осі Oу. y = arcsin (-x)                                                                                                                                                                                                                

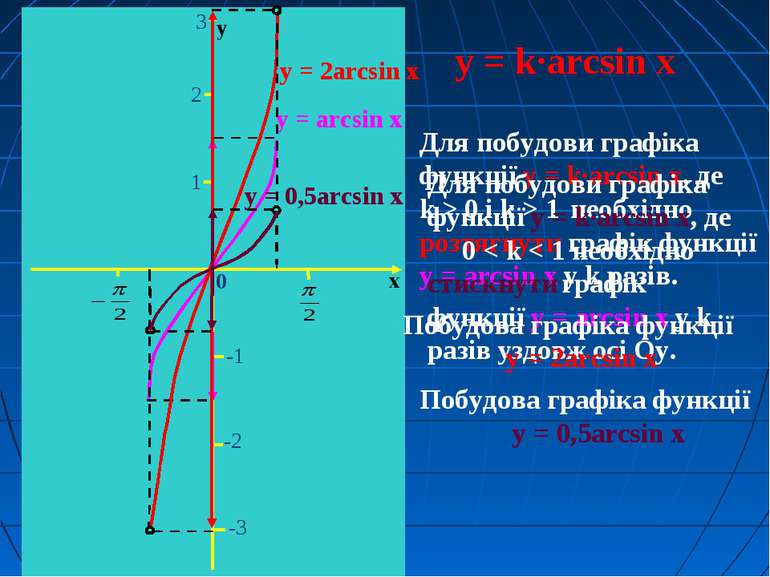
y = k·arcsin x Для побудови графіка функції y = k·arcsin x, де k > 0 і k > 1 необхідно розтягнути графік функції y = arcsin x у k разів. Для побудови графіка функції y = k·arcsin x, де 0 < k < 1 необхідно стискнути графік функції y = arcsin x у k разів уздовж осі Oу. 0 -1 1 2 -2 х у y = arcsin x y = 2arcsin x -3 3 Побудова графіка функції у = 2arcsin x Побудова графіка функції у = 0,5arcsin x у = 0,5arcsin x

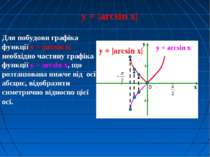
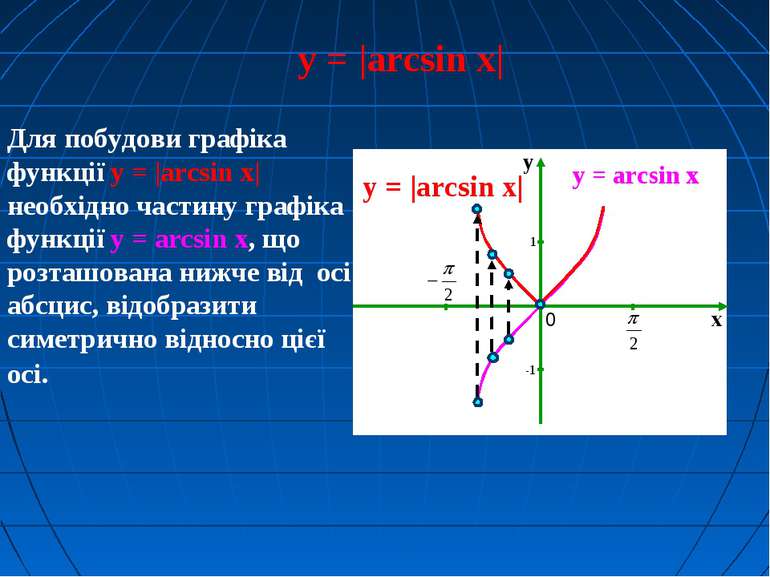
Для побудови графіка функції y = |arcsin x| необхідно частину графіка функції y = arcsin x, що розташована нижче від осі абсцис, відобразити симетрично відносно цієї осі. y = |arcsin x| y = arcsin x y = |arcsin x|                                                                                                                                                                                                                

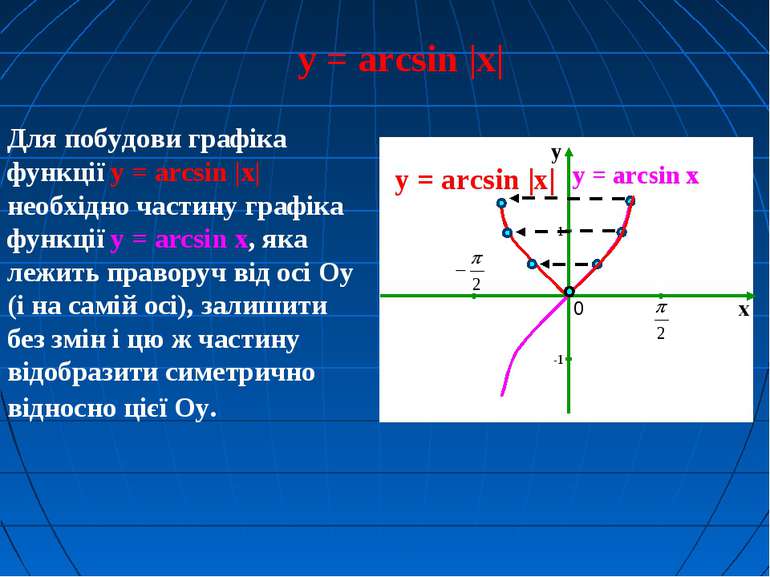
y = arcsin |x| Для побудови графіка функції y = arcsin |x| необхідно частину графіка функції y = arcsin x, яка лежить праворуч від осі Оу (і на самій осі), залишити без змін і цю ж частину відобразити симетрично відносно цієї Оу. y = arcsin x y = arcsin |x|                                                                                                                                                                                                                

Перевір себе 1. Серед наведених функцій вкажіть спадну: а) у = arcsin x + π б) у = arcsin (x + 2) в) у = - arcsin х г) у = |arcsin x| 2. Серед наведених вкажіть функцію, графік якої паралельно перенесли на 2 одиниці вниз вздовж осі Oy і на 7 одиниць вліво вздовж осі Ox. б) у = arcsin (x + 7) - 2 а) у = arcsin x + 2 в) у = arcsin (x - 7) - 2 г) у = arcsin (x - 2) - 7

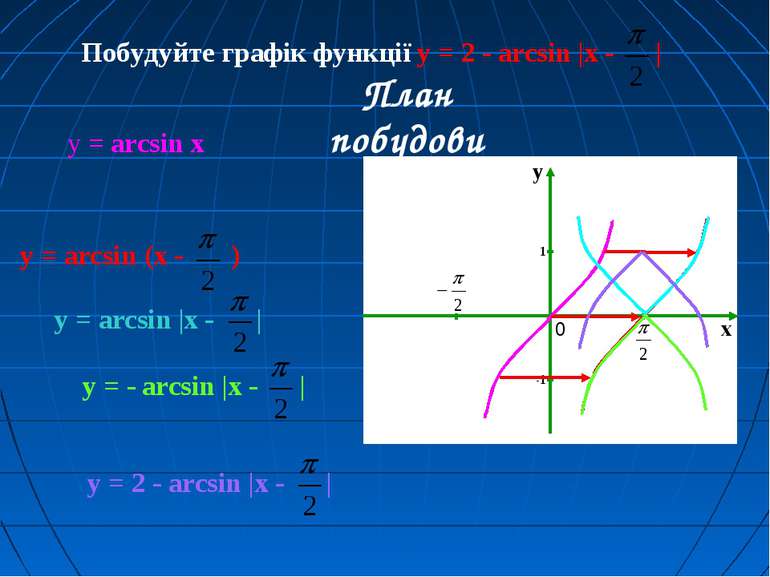
Побудуйте графік функції y = 2 - arcsin |x - | План побудови y = arcsin (x - ) y = arcsin |x - | y = - arcsin |x - | y = 2 - arcsin |x - | у = arcsin x