Презентація на тему:
Логарифми та їх властивості

на тему: «Логарифми та їх властивості» Презентація відкритого заняття з дисципліни “Математика” Підготовлено викладачем-методистом Дзержинського гірничого технікуму Козловою Г.В.

Перевірка домашнього завдання Поясніть правильну відповідь наступних завдань:

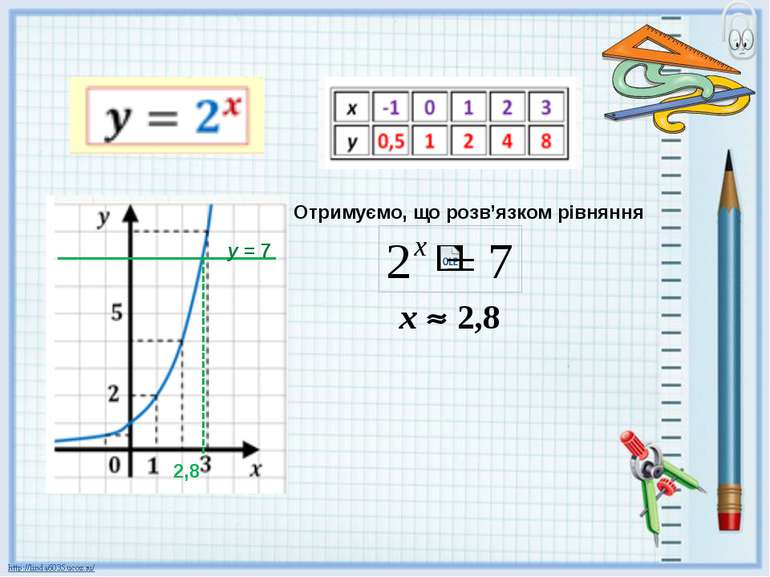
Розв’яжіть рівняння Який вид має рівняння? Чи можна його розв’язати за загальною схемою? Чому? Чи має рівняння корені? Як це аргументувати? Яким наближеним способом можна розв’язати це рівняння? 2х = 7

у = 7 2,8 х 2,8 Отримуємо, що розв’язком рівняння

Тема нашого заняття «Логарифм та його властивості» Логарифми важливі як зручний засіб при дослідженні показникових функцій і розв'язуванні пов'язаних з ними задач. На цьому занятті ми познайомимось з поняттям логарифма, його властивостями, основною логарифмічною тотожністю, будемо вчитися виконувати дії з логарифмами. Таким чином, необхідно вивчити дію, яка дозволяє за поданим значенням степеня додатного числа, що не дорівнює 1, знаходити показник цього степеня.

Слайд з творчого проекту на тему «Практичне застосування логарифмічної та показникової функцій в різних галузях природознавства і математики»

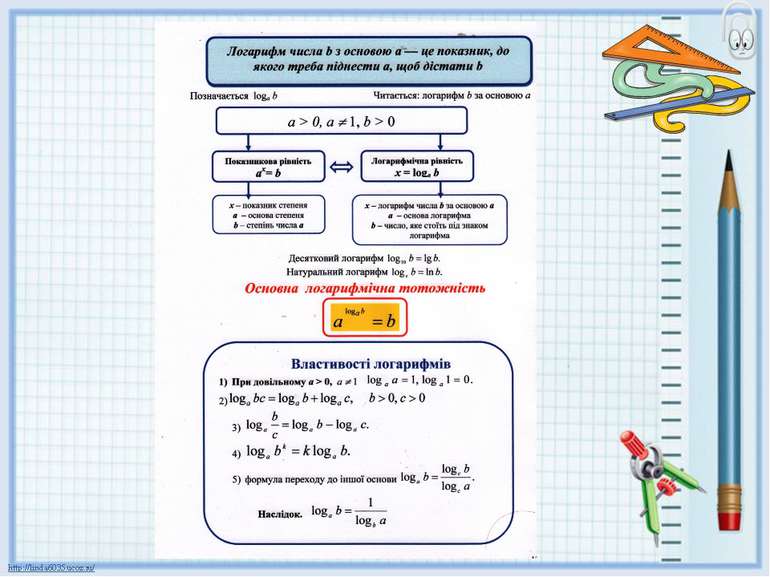
Логарифмом числа b > 0 з основою а, де а > 0, а 1, називається таке число с, що ас = b. Іншими словами, логарифм числа b за основою а — це показник, до якого треба піднести а, щоб дістати b. Символічно записують с = logа b. Таким чином, розв’язком рівняння є число х = log27 Можна сказати, що формули ас = b та с = logа b є рівносильними, оскільки подають одну й ту саму залежність між числами а, b і с.

Приклад. 1) log232 = 5, оскільки 25 = 32; logа b = с, оскільки ас = b Знайти: 1) log232; 2) log3 3) log4 2; 4) log10l.

Десятковий логарифм – це логарифм за основою 10. Наприклад, lg1000 = 3, оскільки 103 = 1000. Позначення Натуральний логарифм – це логарифм за основою е (е – ірраціональне число, )

Основна логарифмічна тотожність Оскільки логарифм числа b з основою а є розв'язком рівняння ах = b , то маємо рівність Приклад

Властивості логарифмів 1) При довільному a > 0, а 1, Ці рівності випливають із співвідношень: а1 = а, а0 = 1. Наприклад, 1) log91 = 0, оскільки 90 = 1; 2) log5x = 0, х = 50 , х = 1. 3) log99 = 1, оскільки 91 = 9.

2) Логарифм добутку двох або кількох чисел дорівнює сумі логарифмів співмножників: Властивості логарифмів Нехай b, с – додатні числа. За основною логарифмічною тотожністю маємо Перемноживши ці рівності, дістанемо з іншого боку що і треба було довести.

Властивості логарифмів Наприклад, 1) ln15 = ln(3 5) = ln3 + ln5; 2) lg20 + lg5 = lg(20 5) = lg100 = 2.

Властивості логарифмів 3) Логарифм частки дорівнює різниці логарифмів чисельника і знаменника: що і треба було довести.

Властивості логарифмів Наприклад,

4) Логарифм степеня дорівнює добутку показника степеня на логарифм основи: Властивості логарифмів що і треба було довести.

Властивості логарифмів Наприклад,

Властивості логарифмів справджується формула: (формула переходу до іншої основи) Наслідок. справджується формула: Для довільних додатних a, b, c, Для довільних додатних a, b,

Как не правы те друзья, что утверждают смело: логарифмы – ерунда, не нужны для дела. Логарифмы – это всё: музыка и звуки, и без них никак нельзя обойтись в науке. Фізика - інтенсивність звуку (децибели). Астрономія – шкала яскравості зірок. Хімія – активність водневих іонів. Сейсмологія – шкала Ріхтера. Теорія музики – нотна шкала по відношенню до частот нотних звуків. Історія – логарифмічна шкала часу.

Закріплення отриманих знань Вправа 1. Усно. Яка з наведених рівностей неправильна? Вправа 2. Усно. Який із наведених виразів не має змісту?

Розв’язок. Вправа 3. Знайдіть логарифми чисел, якщо

Вправа 4. Виразіть 1) lg 12 через lg3 та lg4; Розв’язок. 1) lg 12 = lg(3 4) = lg3 + lg 4; 3) lg8 = lg23=3lg2. 3) lg8 через lg2. через lg7 та lg8;

Вправа 5. Знайдіть значення виразів. 2) lg25 + lg4 = 2) lg25 + lg4=lg25 4=lg100=2;

Робота в парі Критерії оцінювання Кожне завдання оцінюється 1 балом. Якщо ви набираєте 1 - 4 бали, то рівень засвоєння низький, 5-6 – середній, 7-9 – достатній, 10-12 – високий.

Розв'язок завдань 1. Перевірте правильність рівності: 2. Обчисліть:

3. Користуючись основною логарифмічною тотожністю, спростіть вираз: Критерії оцінювання Кожне завдання оцінюється 1 балом. Якщо ви набираєте 1 - 4 бали, то рівень засвоєння низький, 5-6 – середній, 7-9 – достатній, 10-12 – високий.

Повідомлення домашнього завдання. вивчити ОК, [5], Гл.5, § 21, п.4, п.5, виконати вправи 5.12, 5.13 (5-8), 5.14 (3-6) с.207

Систематизація отриманих знань та вмінь Таким чином, після сьогоднішнього заняття ми повинні знати: означення логарифма та його запис; основну логарифмічну тотожність; основні властивості логарифмів; уміти: застосовувати отримані знання до розв’язання вправ

Дякую за заняття