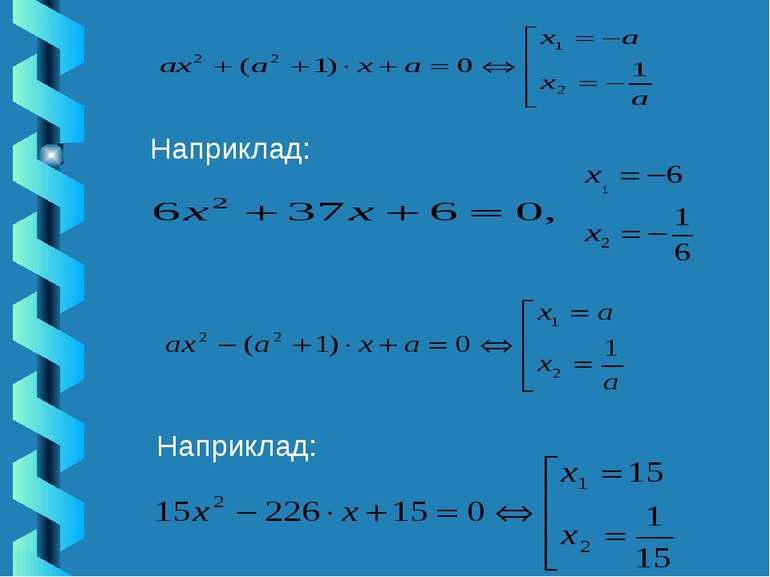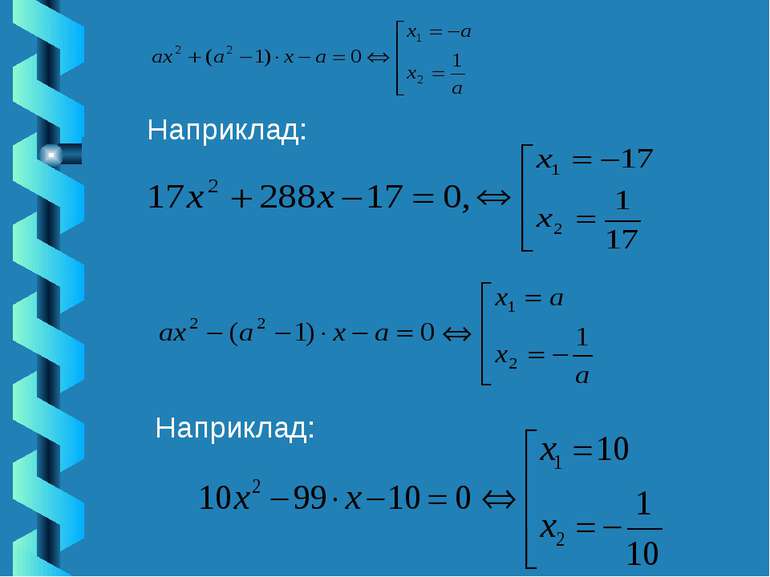Презентація на тему:
Квадратні рівняння. Прийоми усного розв’язування квадратних рівнянь

Прийоми усного розв’язування квадратних рівнянь Таценко А.Г., вчитель математики ЗОШ № 19 м. Черкаси

Квадратні рівняння – це фундамент, на якому зводиться велична будівля алгебри. Квадратні рівняння знаходять широке застосування при розв’язуванні тригонометричних, показникових, ірраціональних рівнянь і нерівностей. В шкільному курсі математики вивчаються формули коренів, за допомогою яких можна розв’язувати будь-яке квадратне рівняння. Однак існують і інші прийоми розв’язування квадратних рівнянь, які дозволяють дуже швидко і раціонально їх розв’язувати.

Прийоми усного розв’язування квадратних рівнянь: 1) 2 ) прийом «коефіцієнтів» 3) прийом «перекидки»

, то Якщо Прийом №1 Прийоми усного розв’язування квадратних рівнянь Наприклад:

Нехай дано квадратне рівняння де 1. Якщо a + b + c=0 ( сума коефіцієнтів рівна нулю), то Доведення: Розділимо обидві частини рівняння на отримаємо зведене квадратне рівняння По теоремі Вієта За умовою a + b +c =0, звідси b= - a – c. Значить, Отримаємо що і потрібно було довести. Доведення прийому №1

Якщо b = a + c, то Прийом №2 Наприклад:

Розв’яжіть рівняння

До якого типу відноситься рівняння Розв’яжіть його. Відповідь: І Р В Н Я Н Н Я

ЗАДАЧА Знайти найбільш раціональним способом корені рівняння

1. 2. 3. 4. Знайди корені

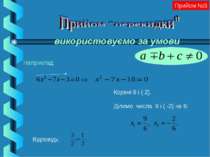
Корені 9 і (-2). Ділимо числа 9 і ( -2) на 6: Відповідь: Прийом №3 використовуємо за умови Наприклад:

Розв’язуємо усно Його корені 10 і 1, і ділимо на 2. Відповідь:

Використовуючи прийоми розв’язання 1) - 3), ви зможете скласти рівняння з раціональними коренями. Наприклад, розглянемо рівняння (Корені 2 і 3), 6 ділиться на 1, 2, 3, 6 6=1*6 6=6*1 6=2*3 6=3*2 Звідси рівняння: ________________ 1) 2) 3) 4) 5) 6) 7) Одне рівняння дало ще 7 рівнянь з раціональними коренями. -------------------------------------------------

Висновок: дані прийоми розв’язання заслуговують на увагу, тому що їх не вивчають в шкільних підручниках математики; потреба у швидкому розв’язуванні обумовлена застосуваннями тестової системи вступних іспитів; оволодіння даними прийомами допоможе економити час і ефективно розв’язувати рівняння;

Прийом «Коефіцієнтів»: 1) Якщо а+b+с=0, то 2) Якщо b = а + с, то 3) Якщо Використовуючи прийоми 1 - 3 можна скласти рівняння з раціональними коренями. , то прийом «Перекидки»

Наприклад: Наприклад:

Наприклад: Наприклад:

Отже: Коли рівняння розв'язуєш ти, Значення кореня слід перевірити. В рівняння його обережно підстав. Коли вірну рівність дістав, То значення кореня ти відшукав. Корінь у нього повинен знайти.