Презентація на тему:
Інтерактивна технологія «мікрофон»

Девіз : Математику не можна вивчати, спостерігаючи як це роблять інші А. Нівен

Лінгвістична гра “Закінчити речення” 1.Областю визначенняD(y)функціїУ=f(x)наз… ТзначенняаргументаХ, при яких функція У=0 2. Областю значень Е(У) функціїУ=f(x)наз… Імножина значень, яких набуває незалежна змінна х 3. Нулями функціїназ… Еквадратичною 4.Функцію де а,b,с -задані дійсні числа, а≠0, х – зміннаназ… Нмножина значень, яких набуває залежна змінна У 5. Лінія, що є графіком квадратичної функції,наз… Рпараболою 6. При а>0вітки параболи напрямлені … Лa(x-x1)(x-x2) 7. При а

Інтерактивна технологія «мікрофон»

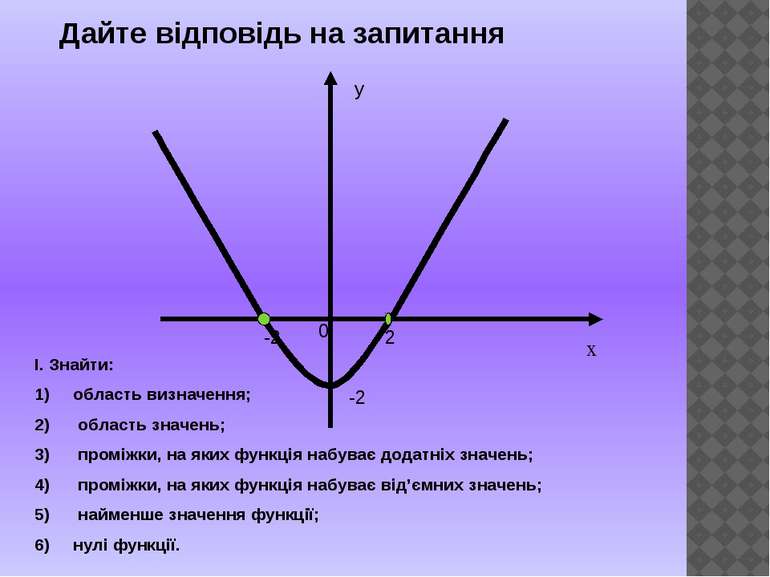
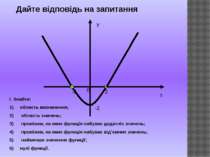
х у 0 -2 2 -2 І. Знайти: область визначення; область значень; проміжки, на яких функція набуває додатніх значень; проміжки, на яких функція набуває від’ємних значень; найменше значення функції; нулі функції. Дайте відповідь на запитання

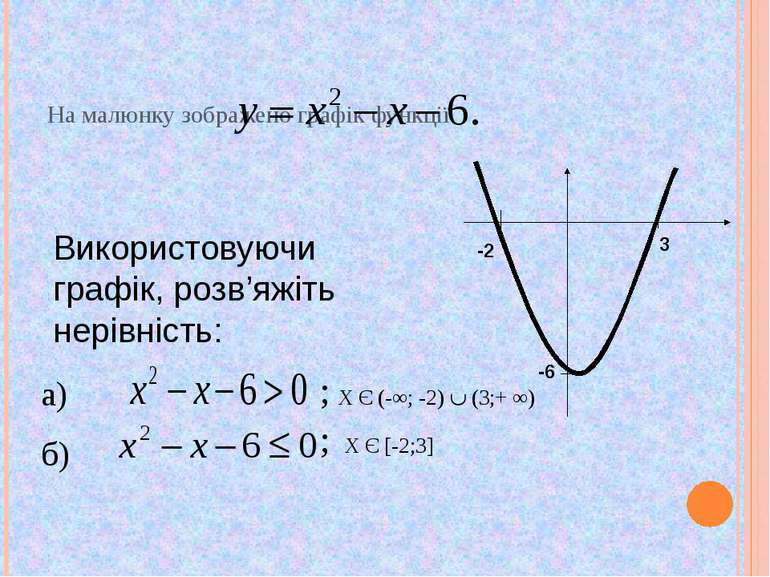
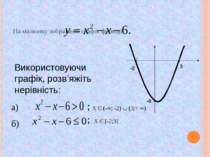
На малюнку зображено графік функції Використовуючи графік, розв’яжіть нерівність: а) б) Х Є (-∞; -2) (3;+ ∞) Х Є [-2;3] ; ;

Тема: «Розв’язування нерівностей методом інтервалів»

Коли квадратний тричлен має два корені, то нерівності ax2+bx+c>0 ax2+bx+c

Алгоритм розв’язування квадратичних нерівностей методом інтервалів 1. Знайти корені квадратного тричлена, розв’язавши рівняння ax2+bx+c=0. 2. Розкласти квадратний тричлен на множники ax2+bx+c=а(х-х1)(х-х2), де х1, х2 - корені . Розглянемо функцію Y = а(х-х1)(х-х2). Знайти D(y). Нанести нулі на область визначення. Визначити знаки функції в кожному інтервалі, на які розбивається область визначення нулями функції. Записати відповідь.

Первинне закріпленням вивченого матеріалу Розв'язати нерівність графічним способом та методом інтервалів Цей підхід можна застосувати для розв’язання нерівностей з будь-якою кількістю множників

Алгоритм розв’язування нерівностей методом інтервалів (x-x1)(x-x2)(x-x3)…(x-xn)

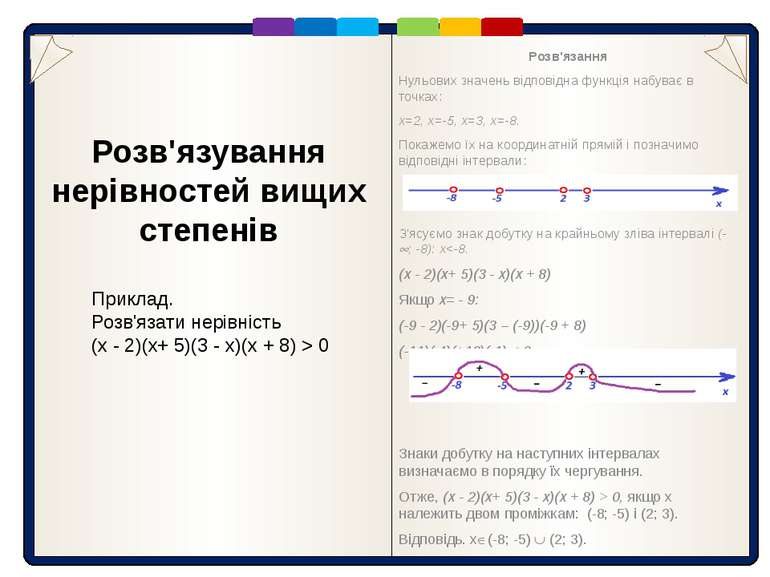
Розв'язання Нульових значень відповідна функція набуває в точках: х=2, х=-5, х=3, х=-8. Покажемо їх на координатній прямій і позначимо відповідні інтервали: З'ясуємо знак добутку на крайньому зліва інтервалі (- ; -8): х 0, якщо х належить двом проміжкам: (-8; -5) і (2; 3). Відповідь. х (-8; -5) (2; 3). Розв'язування нерівностей вищих степенів Приклад. Розв'язати нерівність (x - 2)(x+ 5)(3 - x)(x + 8) > 0

(х+4)(х-2)(х-3)

Розв’язати нерівність: (10х+3)(17-х)(х-5)≥0

Розв’язати

При яких значеннях Х має зміст вираз? (2х-5)(х-3)(х-4)≥0 Відповідь: [2,5;3] [4;+ ).

Гра «Аукціон» 1 команда 2 команда 3 команда 1. 1. 1. 2. 2. 2. 3. 3. 3.

Розуму не позичати Будь найкращим, набувай багатства, але залишайся скромним. Поспішайте творити добро

Домашнє завдання П.5.3 № 283(а, д,е) №285(а)

Запитання для самоперевірки Які квадратні нерівності можна розв'язати методом інтервалів? У чому суть методу інтервалів? Які ще нерівності, крім квадратних, можна розв'язати методом інтервалів?

10