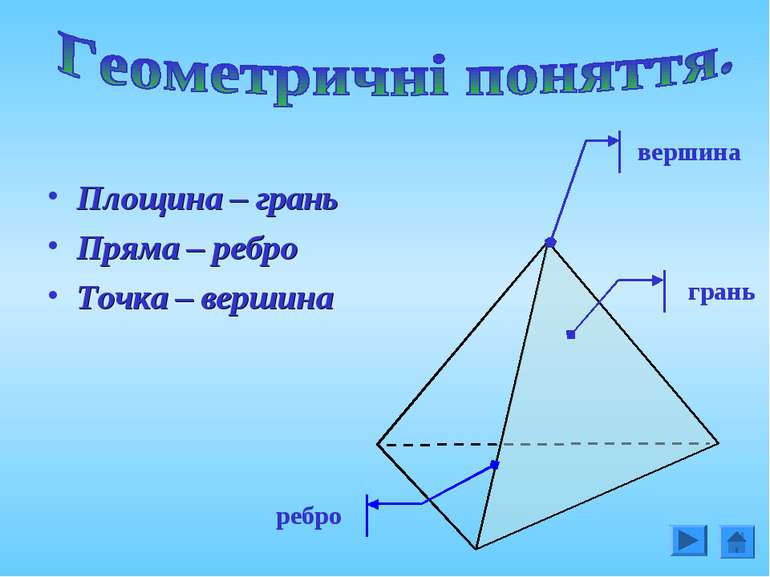
Презентація на тему:
і

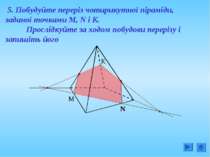
Мета: Повторити геометричні поняття і твердження; навчитися будувати перерізи різними способами; розвивати просторове уявлення та вміння логічно вибудовувати своє пояснення. Виховувати інтерес до технічних знань.

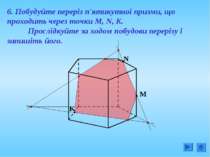
Геометричні поняття; Геометричні твердження; Методи побудови перерізів; Довідковий матеріал; Література; Основні поняття; Побудови перерізів;

грань ребро вершина Площина – грань Пряма – ребро Точка – вершина

Многогранники Тетраедр Паралелепіпед

Якщо дві точки прямої лежать на одній площині, то і вся пряма належить даній площині.

Якщо дві паралельних площини перетинаються третьою площиною, то лінії їх перетину паралельні.

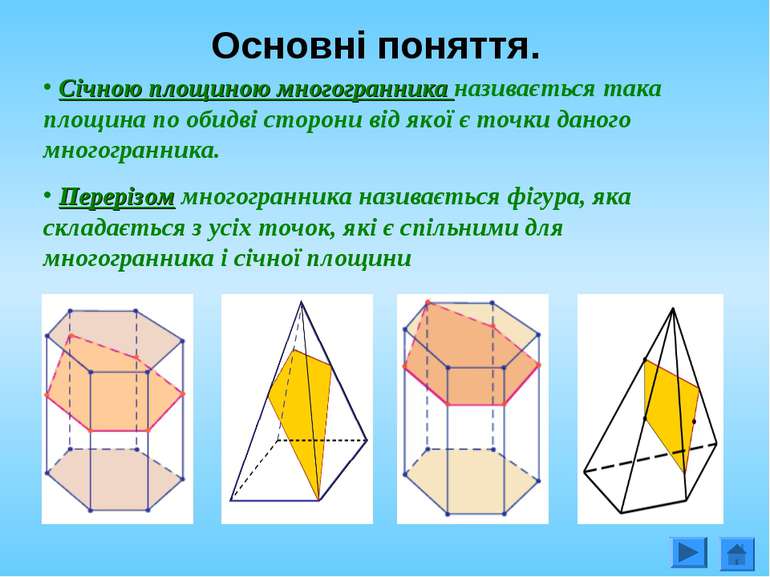
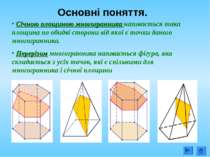
Січною площиною многогранника називається така площина по обидві сторони від якої є точки даного многогранника. Перерізом многогранника називається фігура, яка складається з усіх точок, які є спільними для многогранника і січної площини

Вид перерізу залежить від розміщення площини.

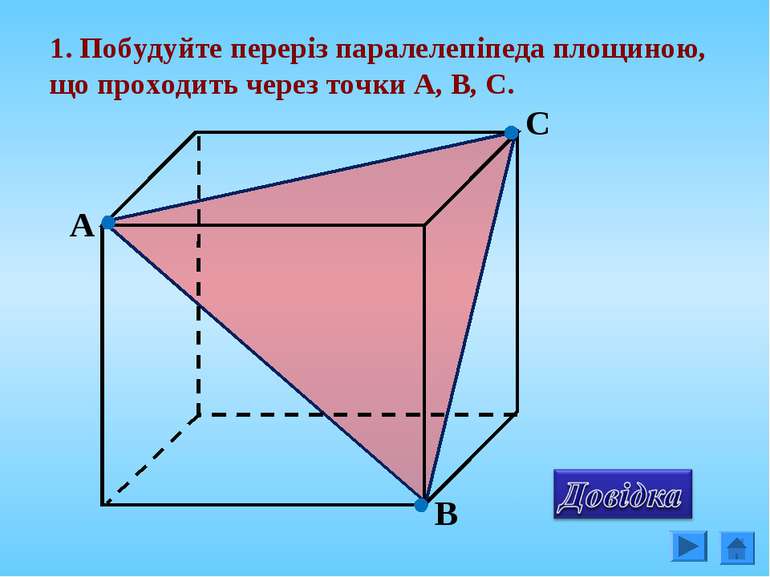
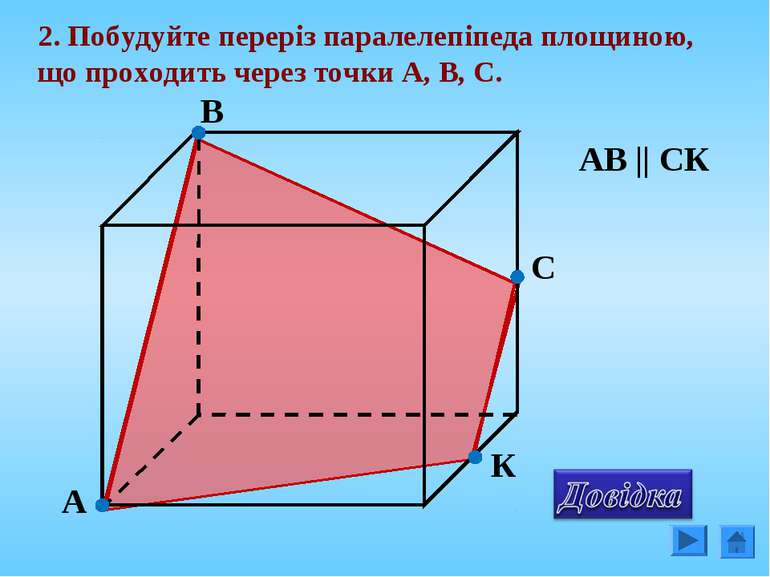
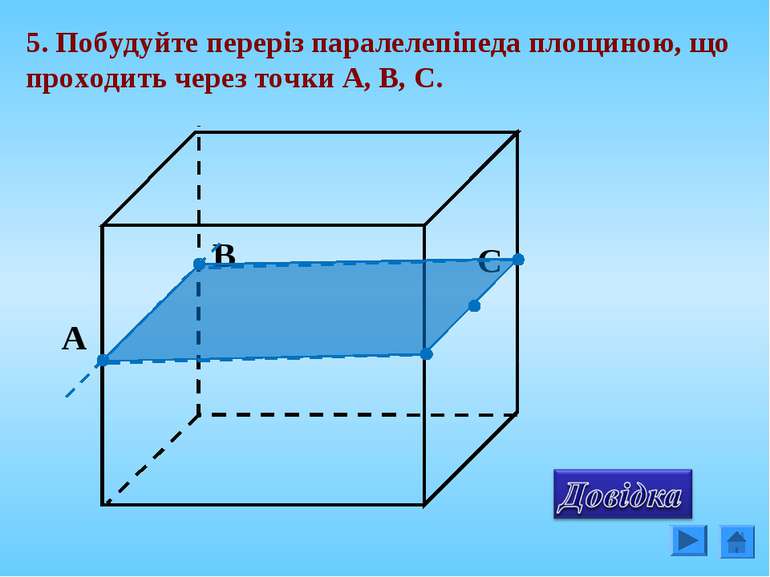
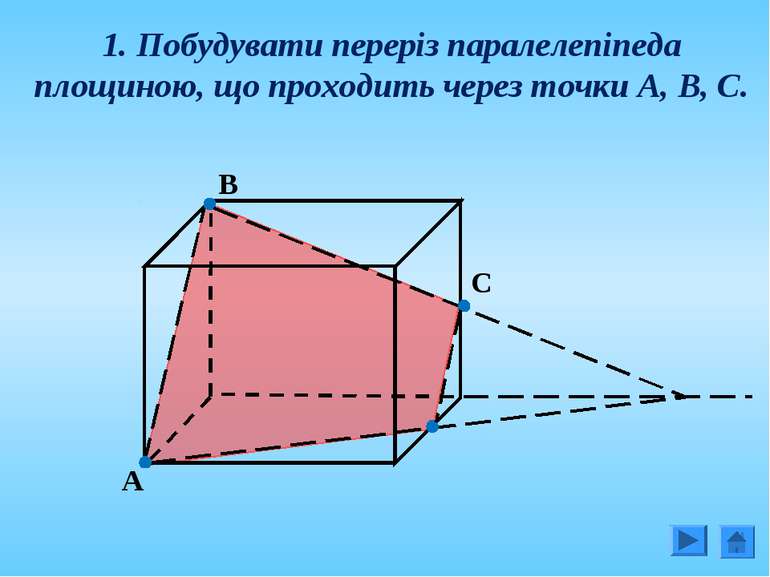
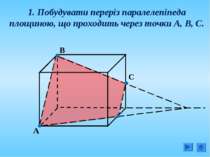
Площину перерізу можна задати: 1. Трьома точками, що не лежать на одній прямій; 2. Прямою і точкою, що не лежить на ній; 3. Двома прямими, що перетинаються; 4. Двома паралельними прямими;

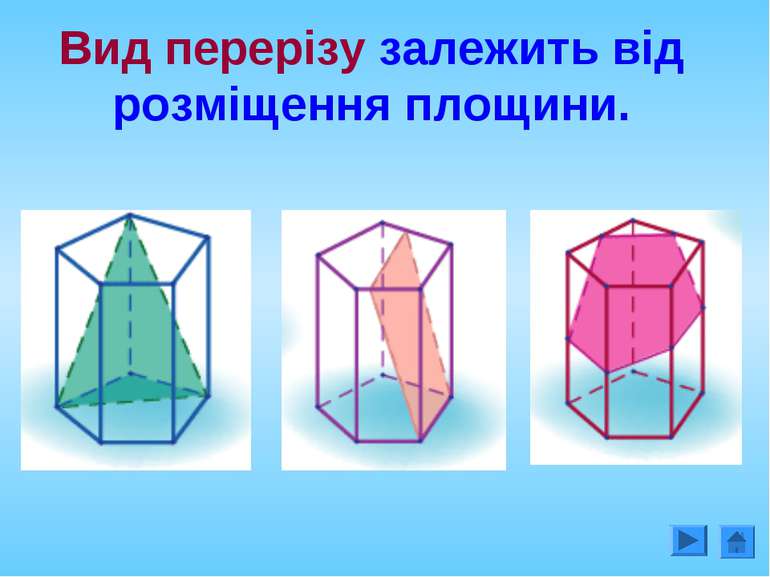
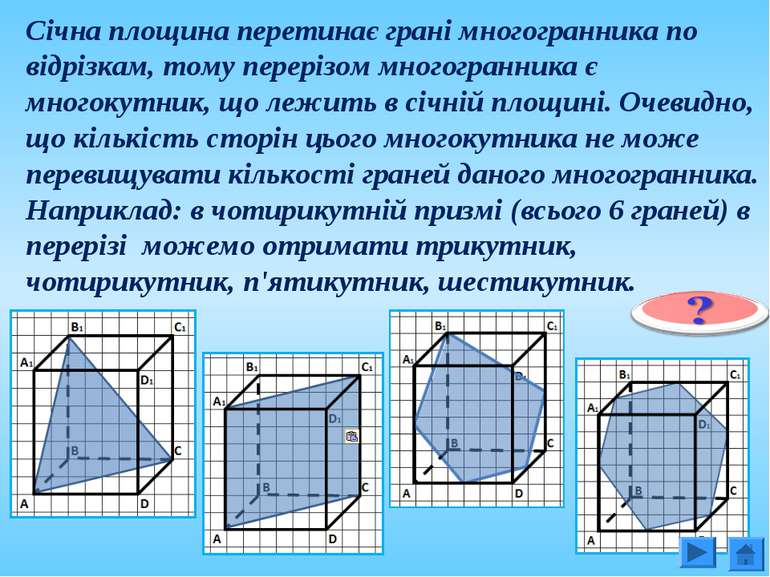
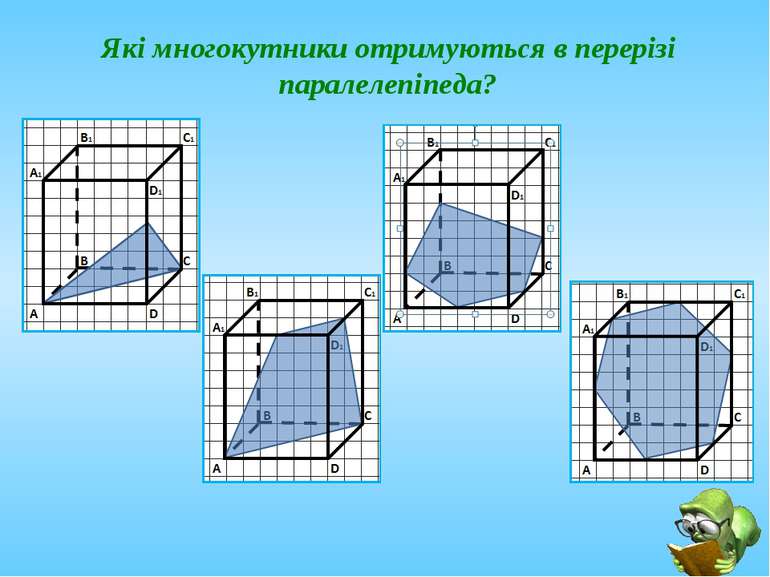
Січна площина перетинає грані многогранника по відрізкам, тому перерізом многогранника є многокутник, що лежить в січній площині. Очевидно, що кількість сторін цього многокутника не може перевищувати кількості граней даного многогранника. Наприклад: в чотирикутній призмі (всього 6 граней) в перерізі можемо отримати трикутник, чотирикутник, п'ятикутник, шестикутник.

Які многокутники отримаємо в перерізі п'ятикутної призми площиною?

Які многокутники отримуються в перерізі паралелепіпеда?

Скільки площин можна провести через виділені елементи?

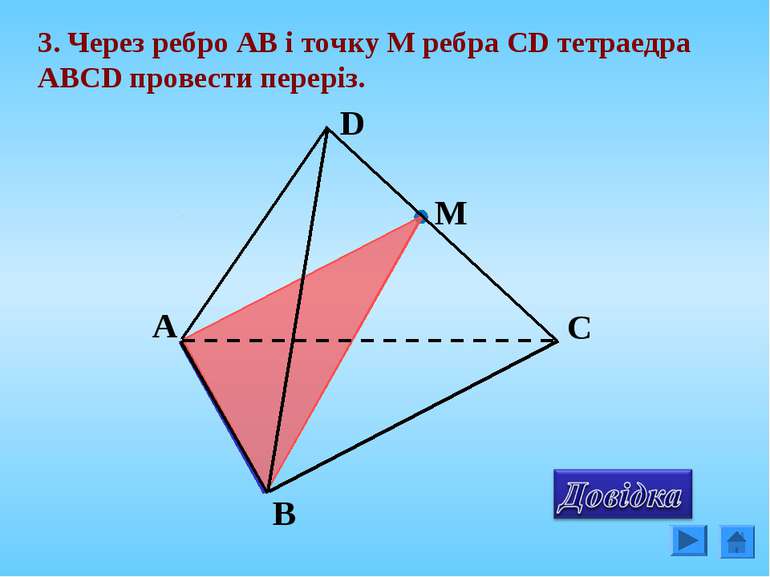
Що означає побудувати переріз? Побудувати переріз многогранника площиною – означає: в площині кожної перетнутої грані вказати дві точки, що належать перерізу; з'єднати ці точки прямою; знайти точки перетину прямої з ребрами многогранника.

1. Побудуйте переріз паралелепіпеда площиною, що проходить через точки А, В, С.

2. Побудуйте переріз паралелепіпеда площиною, що проходить через точки А, В, С. К АВ || СК

3. Через ребро АВ і точку М ребра СD тетраедра АВСD провести переріз. М

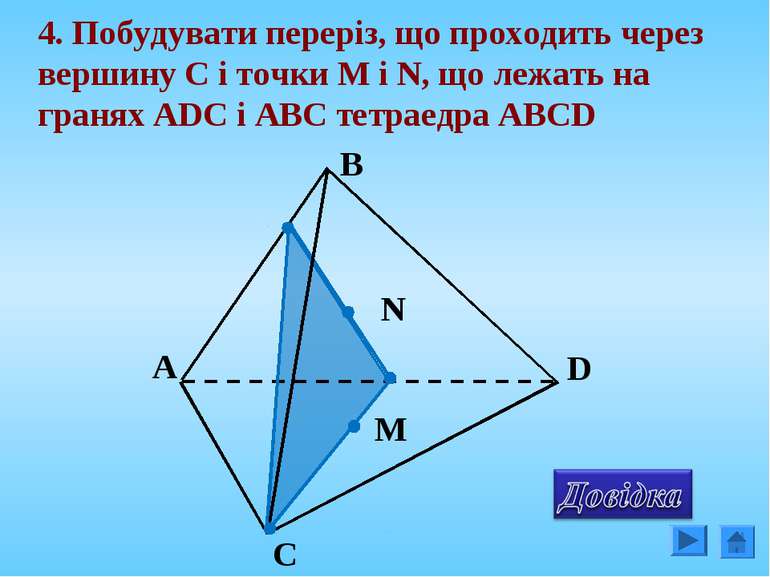
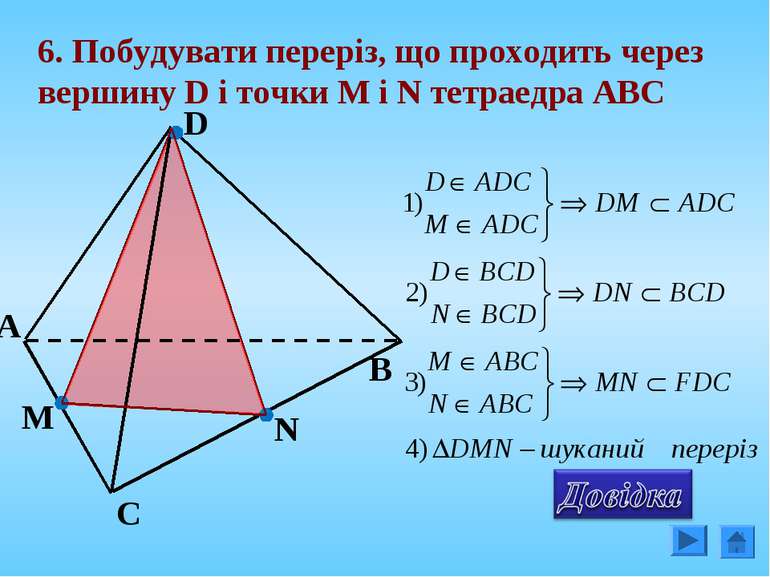
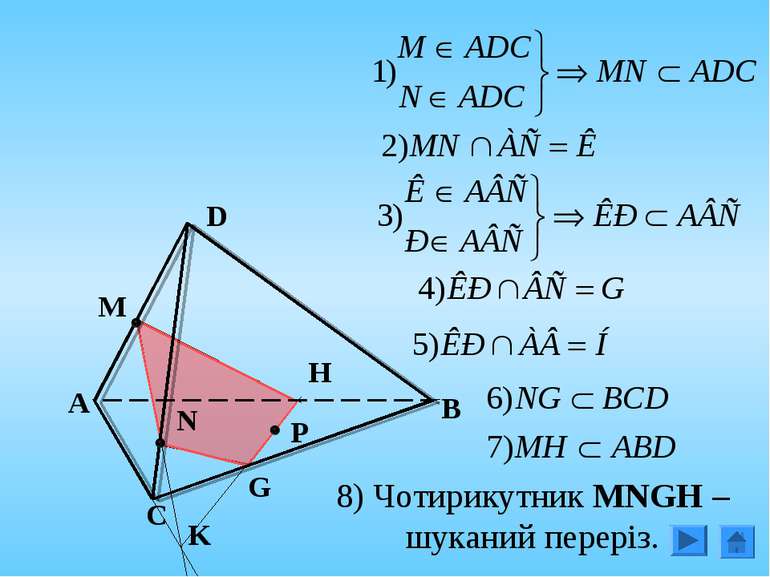
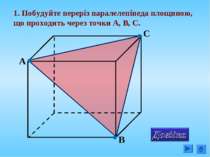
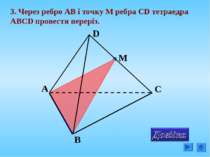
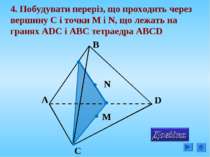
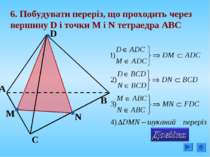
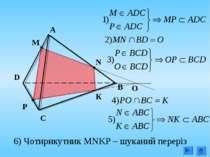
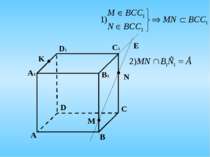
4. Побудувати переріз, що проходить через вершину C і точки М і N, що лежать на гранях ADC і АВС тетраедра АВCD N M

5. Побудуйте переріз паралелепіпеда площиною, що проходить через точки А, В, С.

6. Побудувати переріз, що проходить через вершину D і точки М і N тетраедра АВС N M

Методи побудови перерізів многогранників. Метод слідів. Метод внутрішнього проектування або метод допоміжних перерізів Комбінований метод

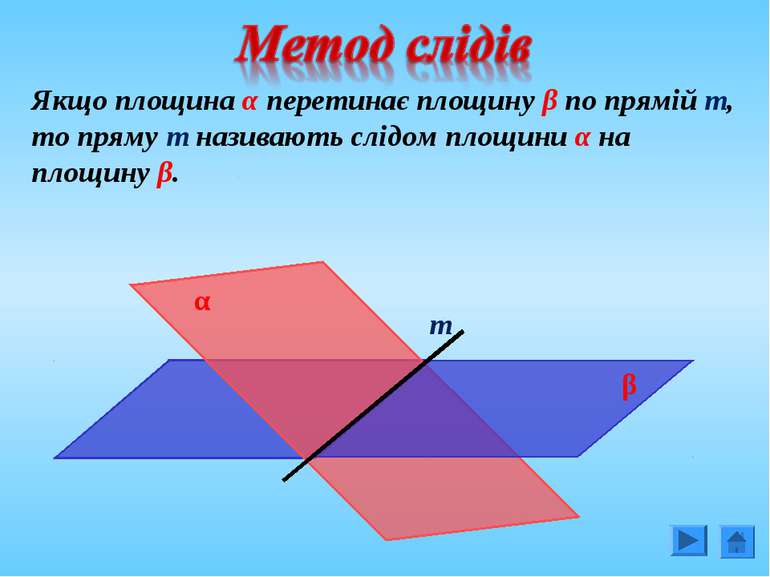
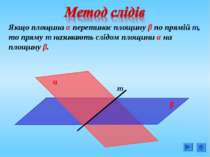
Якщо площина α перетинає площину β по прямій т, то пряму т називають слідом площини α на площину β. α β т

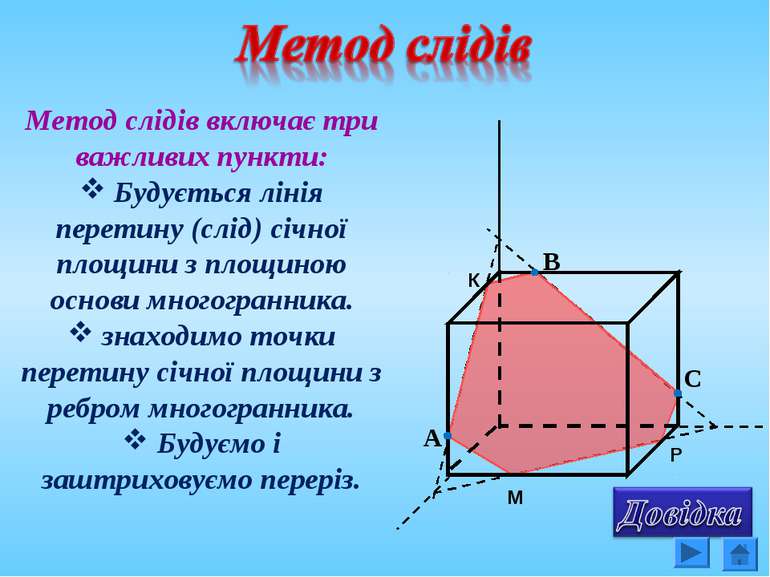
Метод слідів включає три важливих пункти: Будується лінія перетину (слід) січної площини з площиною основи многогранника. знаходимо точки перетину січної площини з ребром многогранника. Будуємо і заштриховуємо переріз. М К Р

Задачі на побудову перерізів методом сліду. Поетапна побудова перерізів; По заданій побудові записати етапи; Складні приклади перерізів;

1. Побудувати переріз паралелепіпеда площиною, що проходить через точки А, В, С. А С В

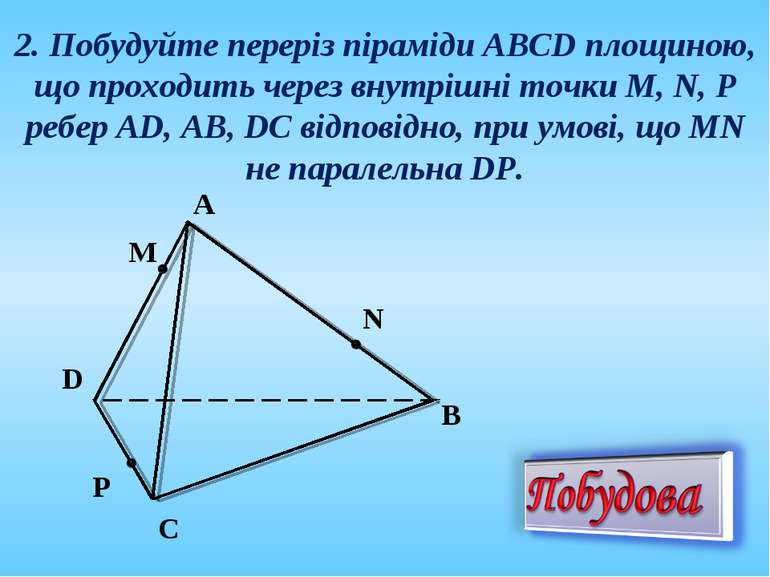
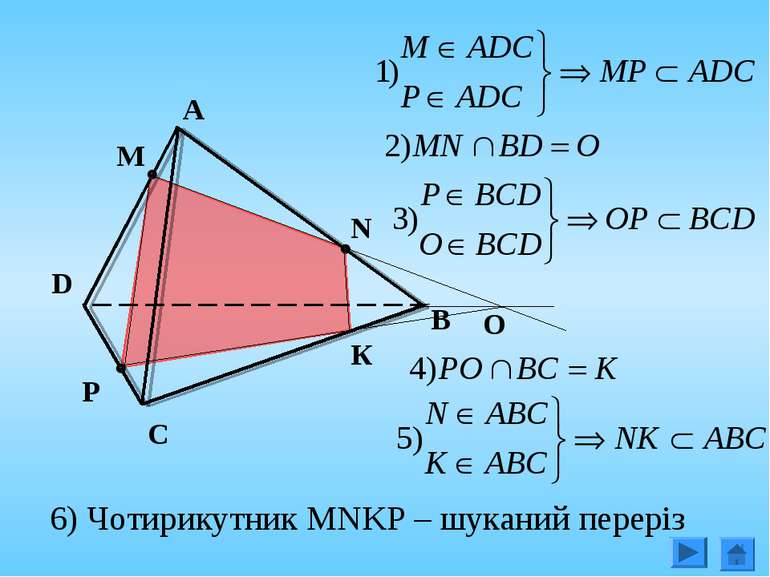
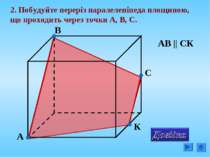
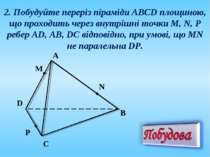
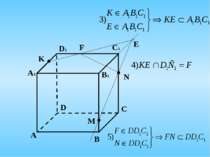
2. Побудуйте переріз піраміди АВСD площиною, що проходить через внутрішні точки M, N, P ребер AD, AB, DC відповідно, при умові, що MN не паралельна DP. A P C N M D B

A P C N M D B О К 6) Чотирикутник MNKP – шуканий переріз

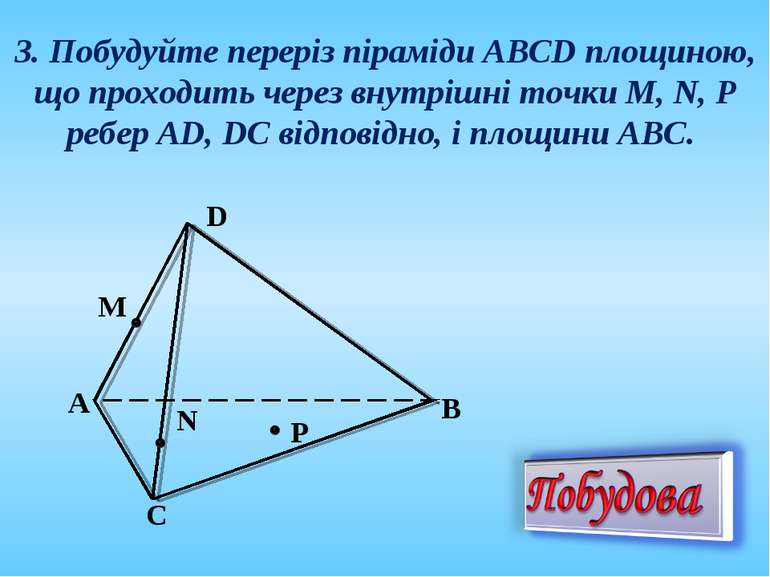
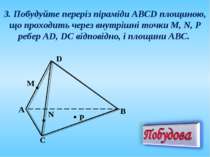
3. Побудуйте переріз піраміди АВСD площиною, що проходить через внутрішні точки M, N, P ребер AD, DC відповідно, і площини АВС.

K H G 8) Чотирикутник MNGH – шуканий переріз.

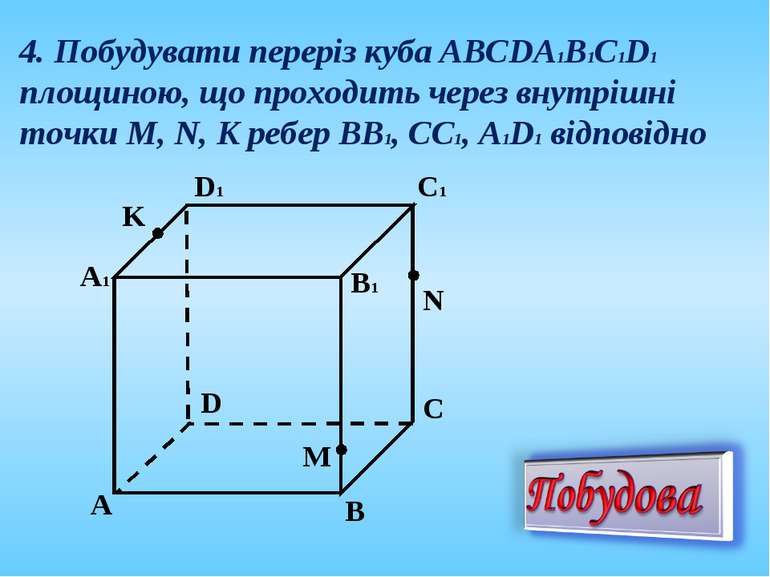
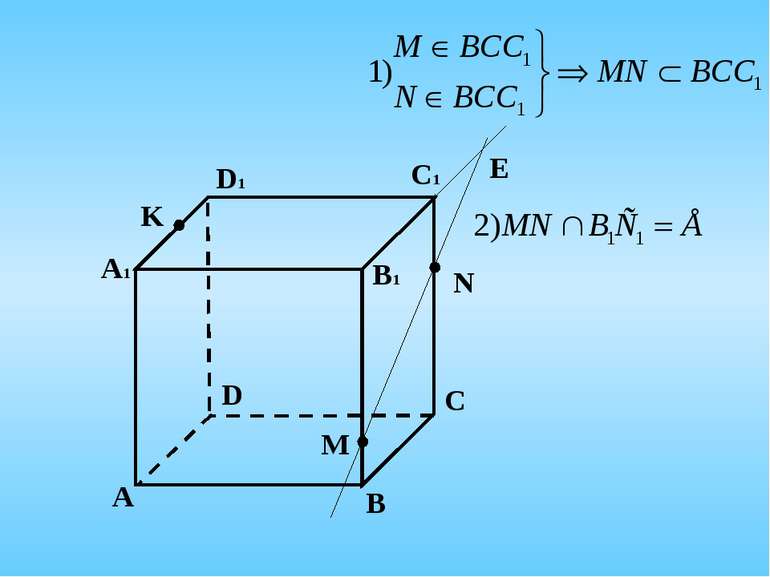
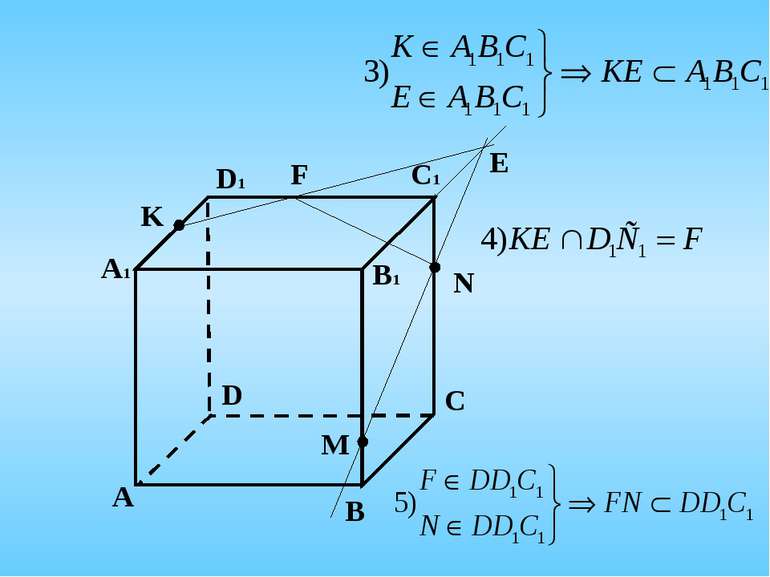
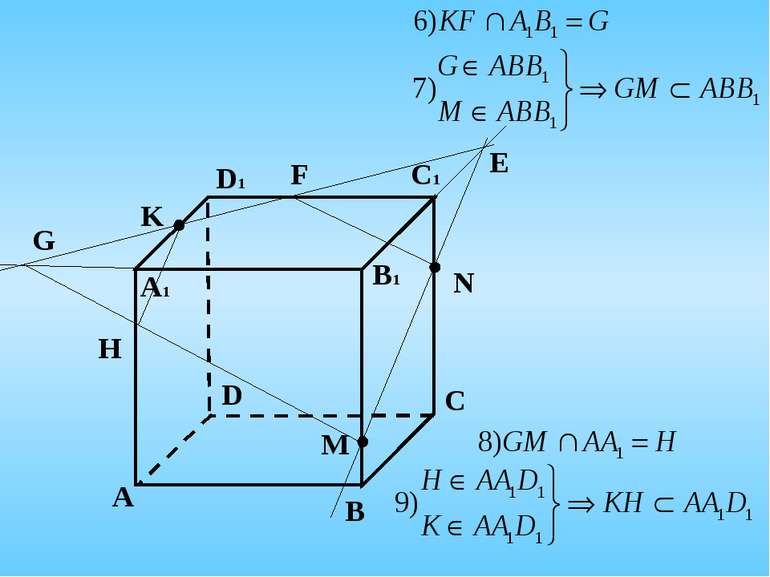
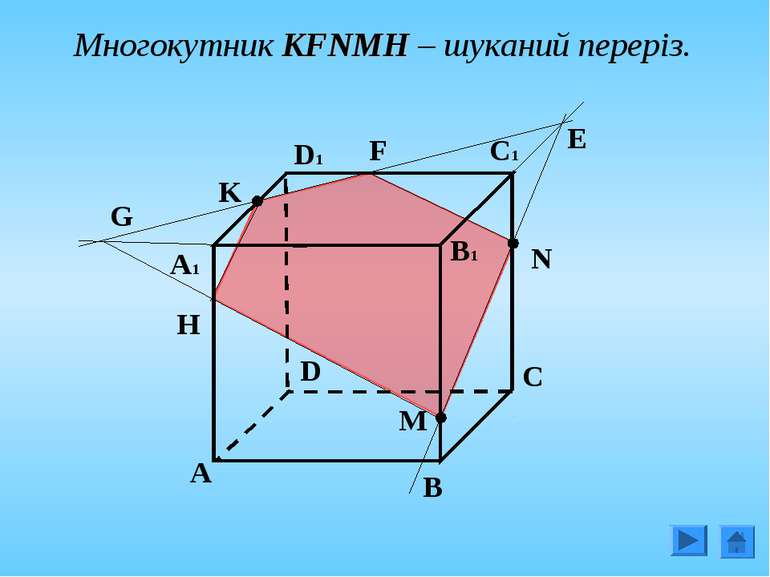
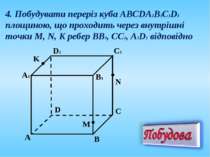
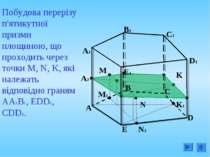
4. Побудувати переріз куба АВСDА1В1С1D1 площиною, що проходить через внутрішні точки M, N, K ребер BB1, CC1, A1D1 відповідно А C B D А1 D1 C1 B1 K N M

А C B D А1 D1 C1 B1 K N M Е

F

G H

F G H Многокутник KFNMH – шуканий переріз.

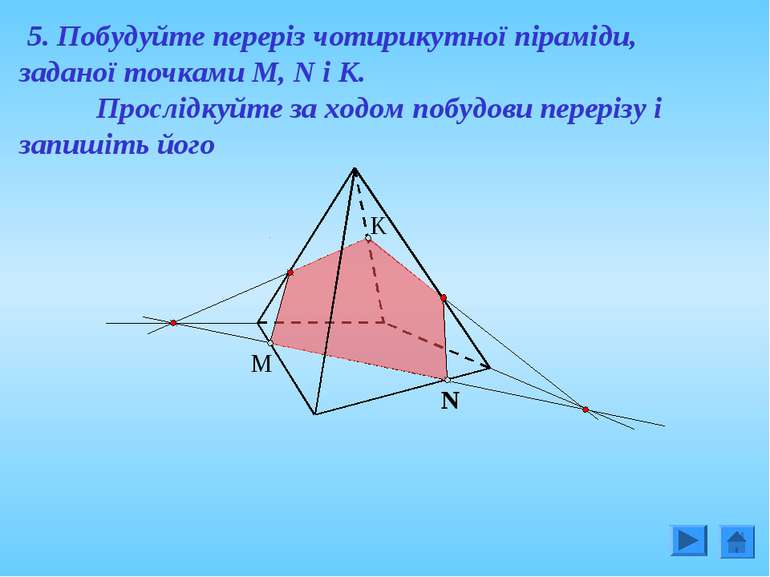
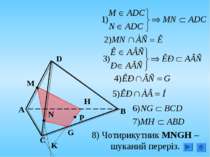
M N K 5. Побудуйте переріз чотирикутної піраміди, заданої точками М, N і К. Прослідкуйте за ходом побудови перерізу і запишіть його

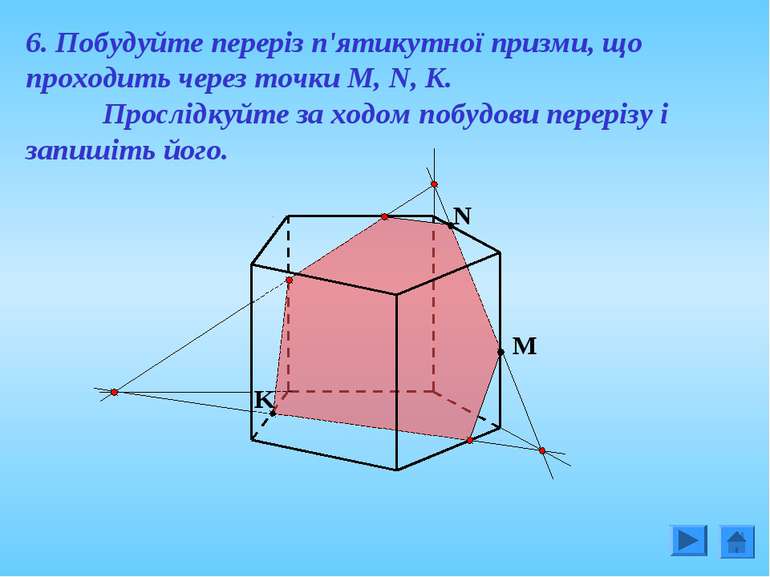
M N K 6. Побудуйте переріз п'ятикутної призми, що проходить через точки M, N, K. Прослідкуйте за ходом побудови перерізу і запишіть його.

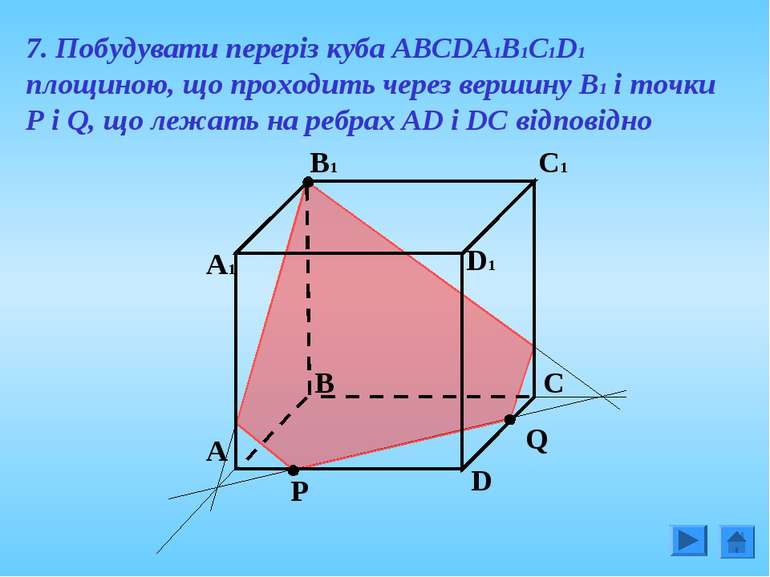
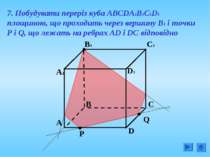
7. Побудувати переріз куба АВСDА1В1С1D1 площиною, що проходить через вершину В1 і точки Р і Q, що лежать на ребрах AD і DC відповідно А Q В P D С А1 В1 D1 С1

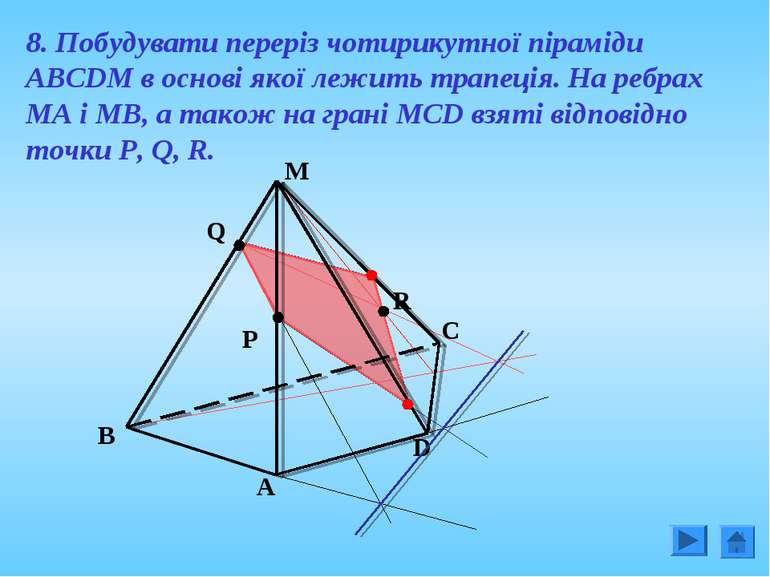
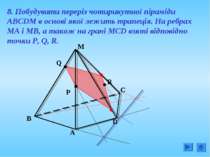
8. Побудувати переріз чотирикутної піраміди АВСDM в основі якої лежить трапеція. На ребрах МА і МВ, а також на грані МСD взяті відповідно точки Р, Q, R.

M N K Розглянемо більш складні приклади.

M N K Пам'ятаємо про те, що вершина піраміди – спільна точка для всіх бічних граней Розглянемо більш складні приклади.

K M N Розглянемо більш складні приклади.

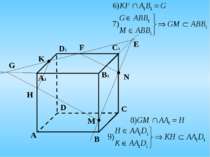
M Метод внутрішнього проектування X Y A A1 N M1 N1 T D1=T1 B C D E E1 C1 B1 Це метод використовується при побудові перерізів в тих випадках, коли незручно знаходити слід січної площини, наприклад, слід знаходиться дуже далеко від заданої фігури

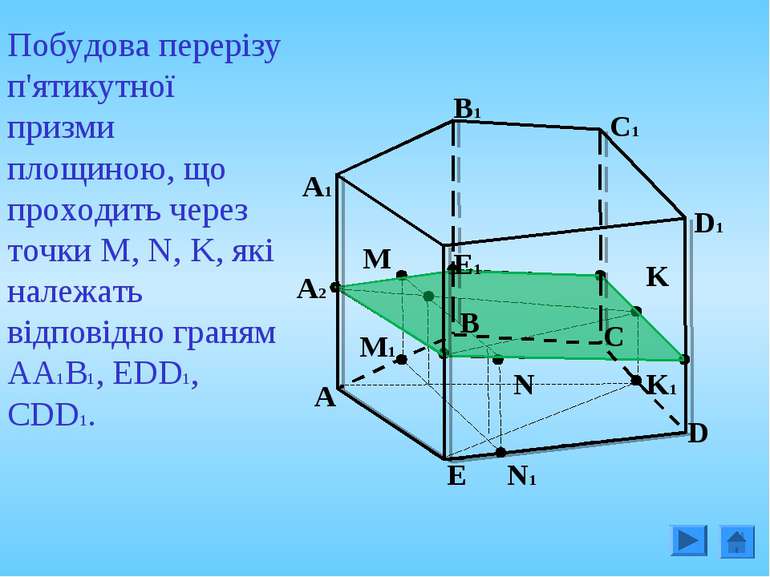
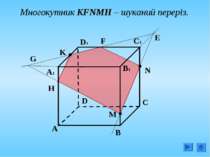
Побудова перерізу п'ятикутної призми площиною, що проходить через точки M, N, K, які належать відповідно граням АА1В1, ЕDD1, CDD1. A C B M D E A1 C1 B1 D1 E1 K N M1 N1 K1 A2

Комбінований метод. При побудові перерізу цим методом на яких етапах побудови використовуються прийоми методі слідів або метода внутрішнього проектування, а на інших етапах використовуються теореми вивченні в розділі “Паралельність прямих і площин!”

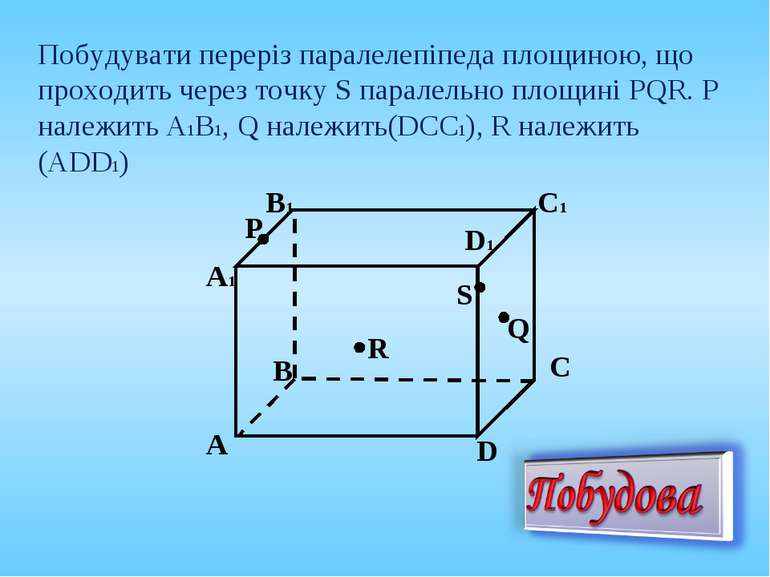
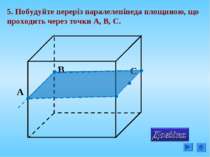
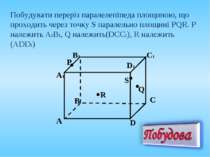
Побудувати переріз паралелепіпеда площиною, що проходить через точку S паралельно площині PQR. P належить А1В1, Q належить(DCC1), R належить (АDD1) Q P R S

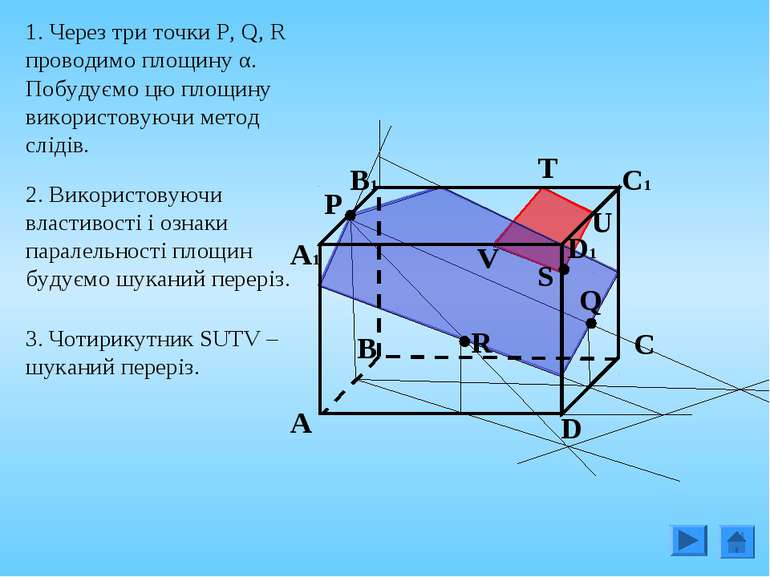
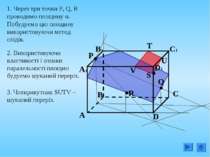
1. Через три точки P, Q, R проводимо площину α. Побудуємо цю площину використовуючи метод слідів. Q P R S 2. Використовуючи властивості і ознаки паралельності площин будуємо шуканий переріз. V T U 3. Чотирикутник SUTV – шуканий переріз.

Довідковий матеріал. Аксіома 1. Через будь-які три точки, що не лежать на одній прямій можна провести площину і до того ж тільки одну; Аксіома 2. Якщо дві точки прямої належать площині, то всі точки даної прямої належать площині; Аксіома 3. Якщо дві площини мають спільну точку, то вони мають спільну пряму на якій лежать спільні точки цих площин; Наслідки з аксіом: Через пряму і точку, що не належить даній прямій можна провести площину і до того ж тільки одну; Через дві прямі, що перетинаються можна провести площину і до того ж тільки одну. Теорема (ознака паралельності двох площин). Якщо дві прямі, що перетинаються однієї площини відповідно паралельні двом прямим, що перетинаються іншої площини, то ці площини паралельні; Теорема (властивість паралельних площин). Якщо дві паралельні площини перетнуто третьою, то лінії їх перетину паралельні; Теорема (ознака паралельності прямої і площини). Якщо пряма, що не належить даній площині, паралельна будь-які прямій цієї площини, то вона паралельна і даній площині.

Література. Е.К.Лейнартас “Математика. Перерізи многогранників”, Красноярск, 2006 http://www.freeware.ru/program_prog_id_1536.html (програма, для побудови перерізів основних просторових фігур) http://mail.spb.fio.ru/archive/group14/c4wu5/tityl.html