Презентація на тему:
Функція

Тема 3 Функція. Квадратична функція Поняття квадратичної функції. Графік функції y=x2+n. Графік функції y=(x+m)2 Графік функції y=(x+m)2+n. Графік функції y=ax2 Графік функції y=a(x+m)2+n Графік функції y=ax2+bx+c Властивості квадратичної функції Найпростіші перетворення графіків функцій Розв’язування вправ. Самостійна робота Розв'язування вправ

Пункт 3.6. Графік функції y=a(x+m)2+n

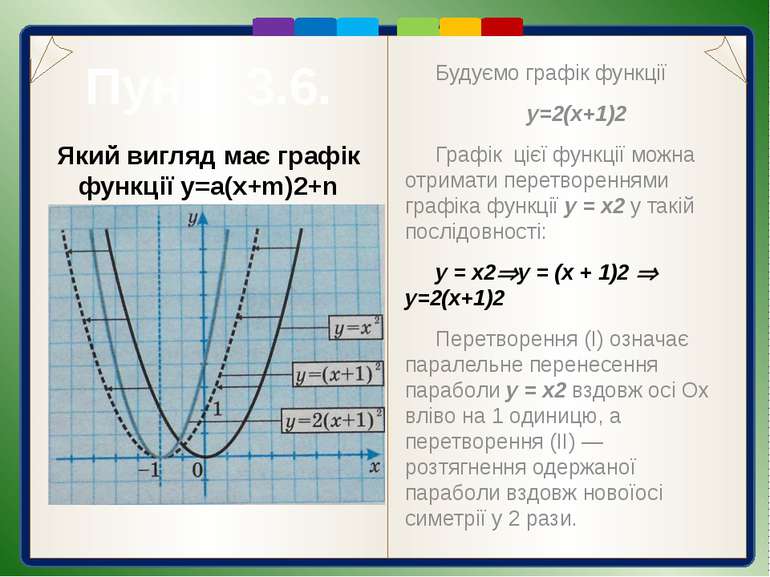
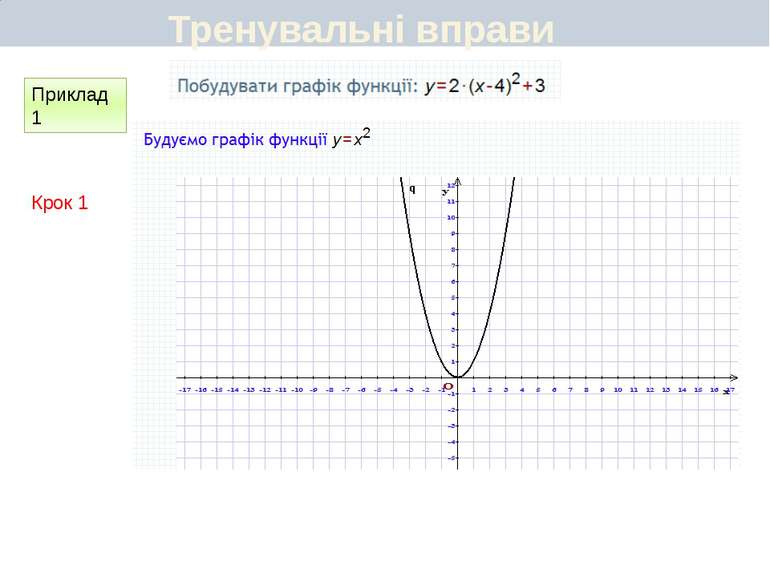
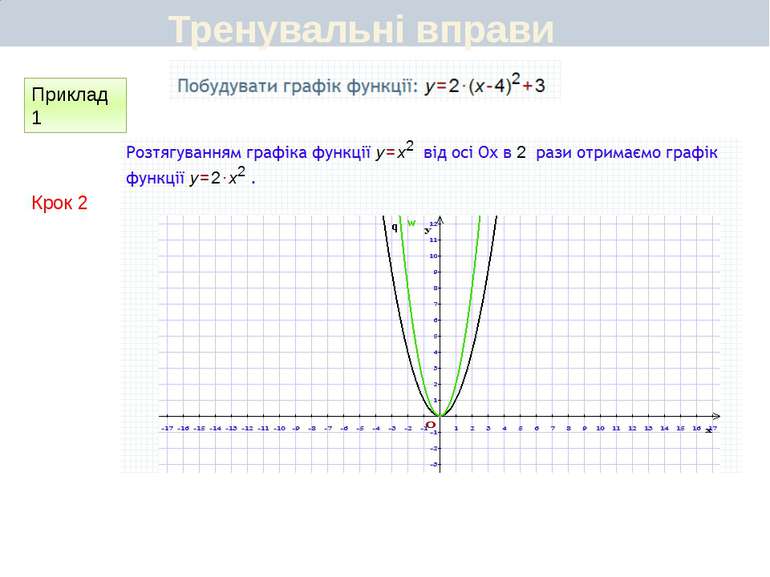
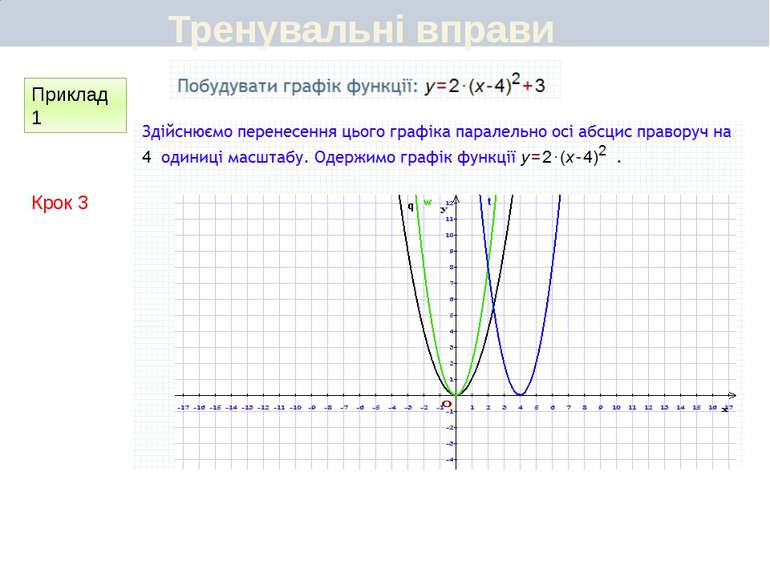
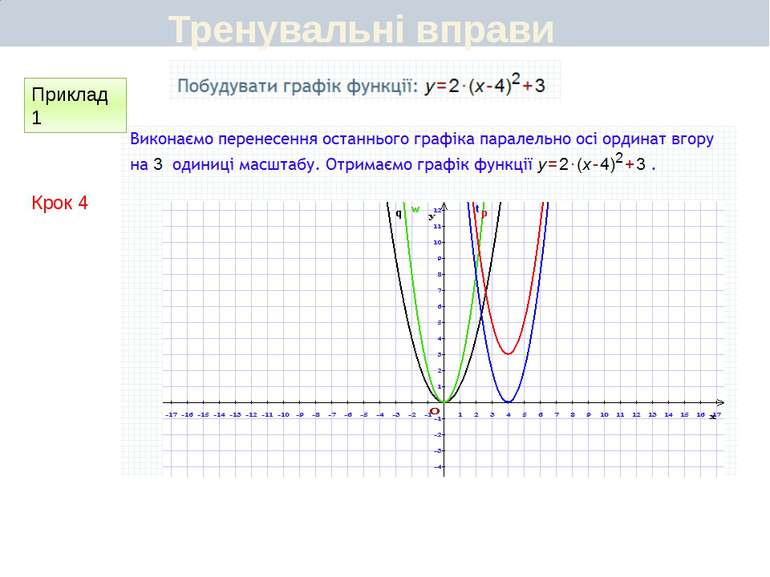
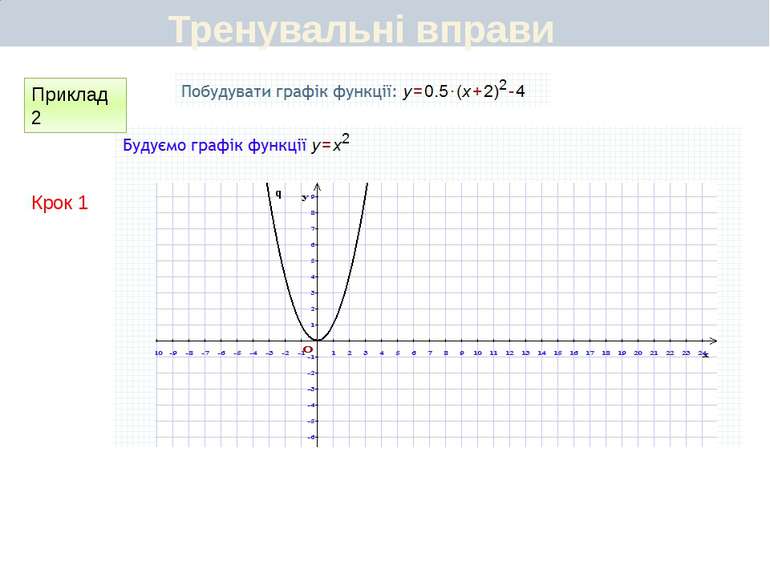
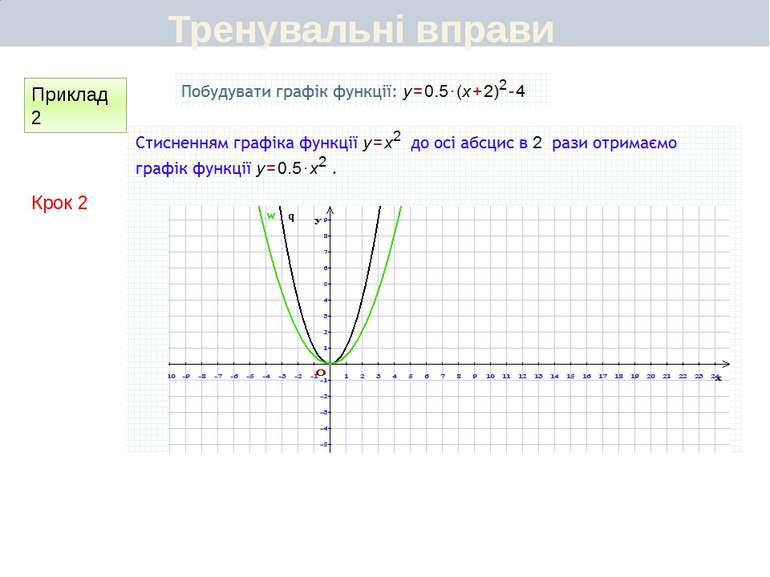
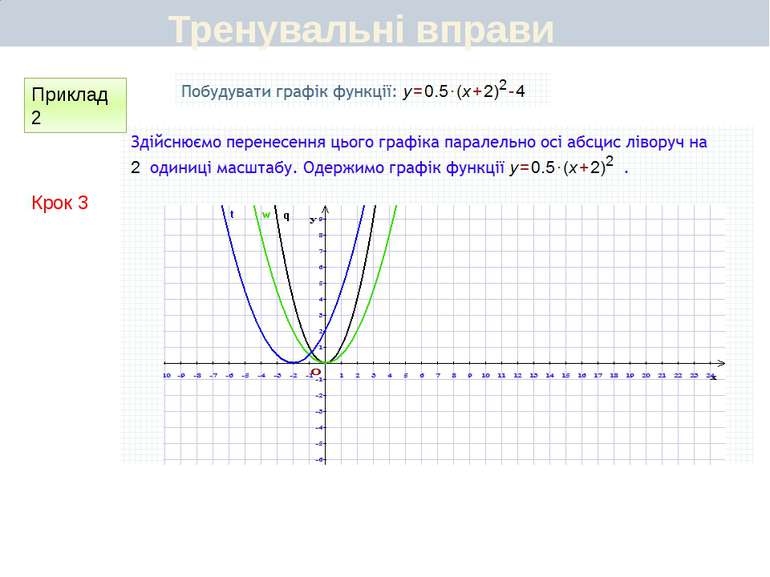
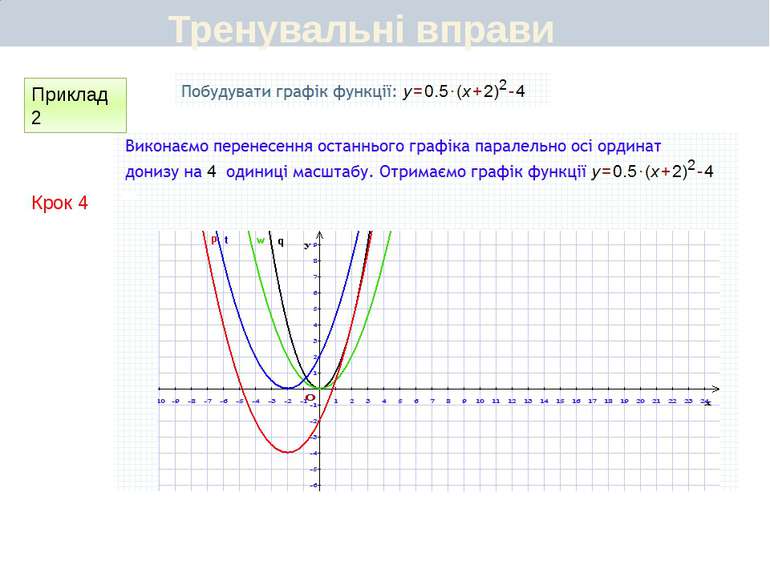
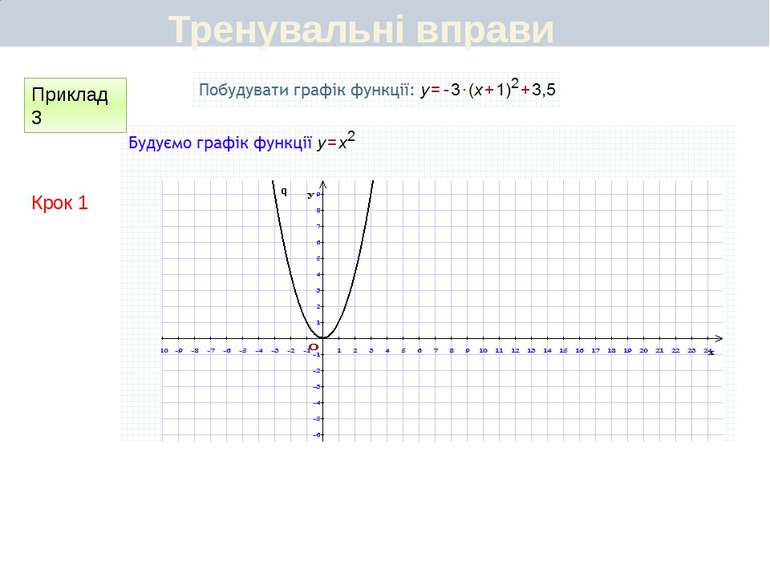
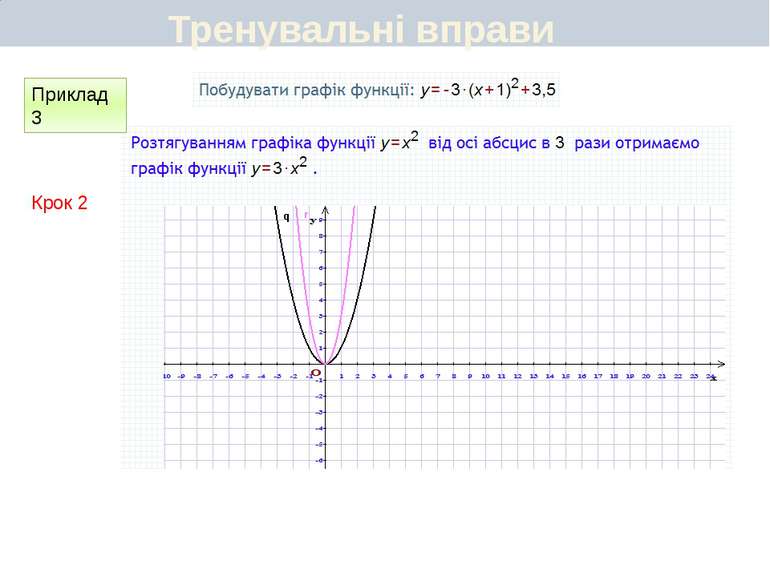
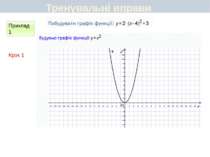
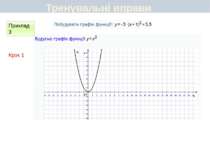
Пункт 3.6. Будуємо графік функції y=2(x+1)2 Графік цієї функції можна отримати перетвореннями графіка функції у = х2 у такій послідовності: у = х2 у = (х + 1)2 y=2(x+1)2 Перетворення (І) означає паралельне перенесення параболи у = х2 вздовж осі Oх вліво на 1 одиницю, а перетворення (ІІ) — розтягнення одержаної параболи вздовж новоїосі симетрії у 2 рази. Який вигляд має графік функції y=a(x+m)2+n

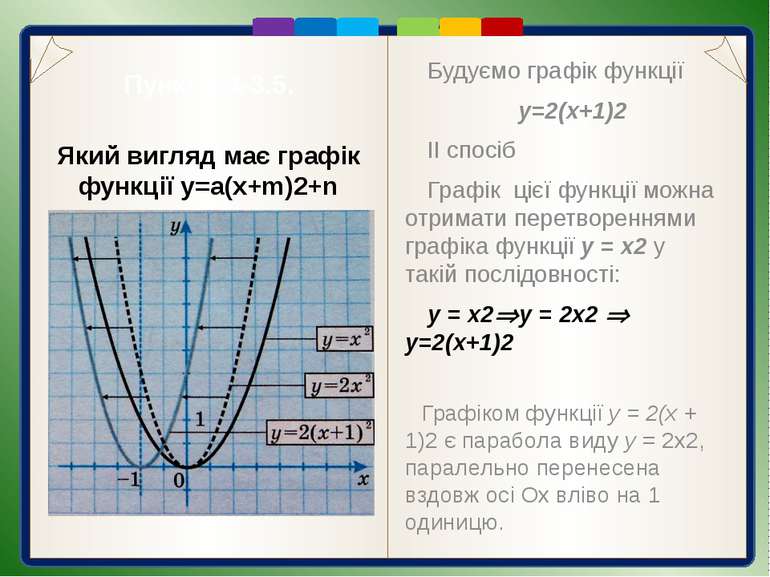
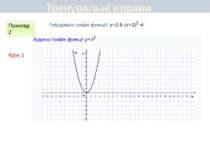
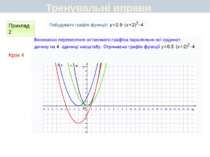
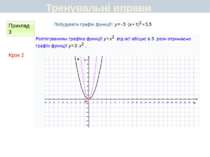
Пункт 3.4-3.5. Будуємо графік функції y=2(x+1)2 ІІ спосіб Графік цієї функції можна отримати перетвореннями графіка функції у = х2 у такій послідовності: у = х2 у = 2х2 y=2(x+1)2 Графіком функції у = 2(х + 1)2 є парабола виду у = 2х2, паралельно перенесена вздовж осі Ох вліво на 1 одиницю. Який вигляд має графік функції y=a(x+m)2+n

Пункт 3.4-3.5. Висновок: Графіком функції у=а(х+т)2 є парабола виду у = ах2 з координатами вершини (0; -т). Який вигляд має графік функції y=a(x+m)2

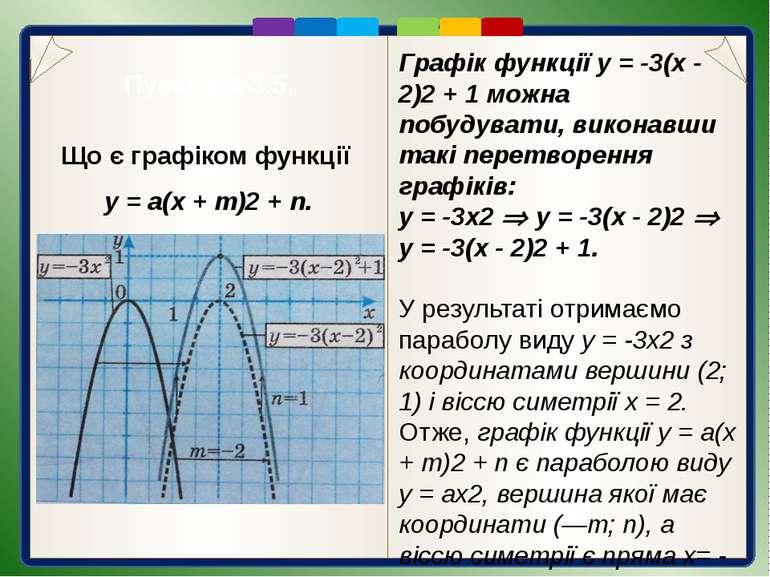
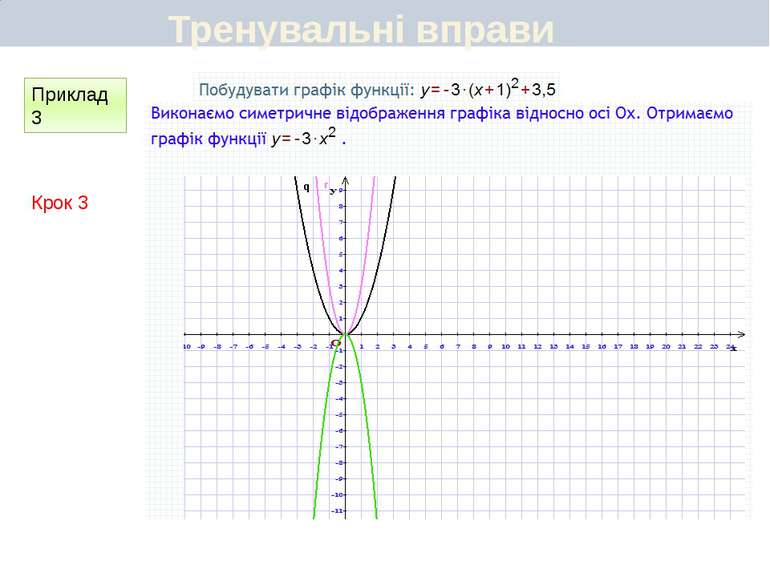
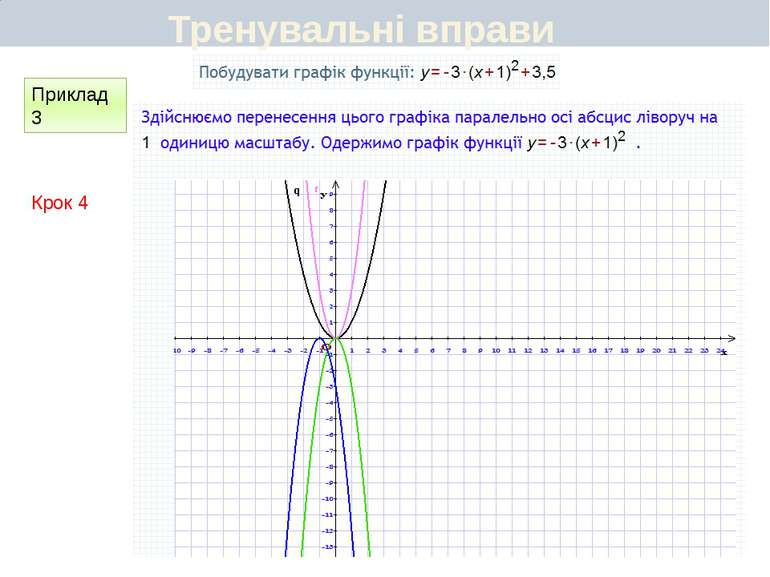
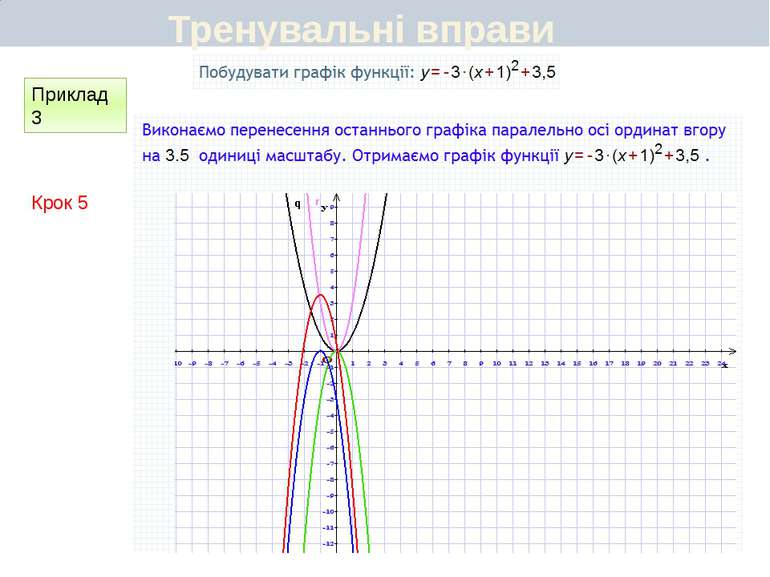
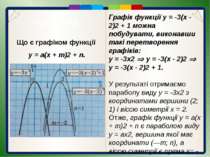
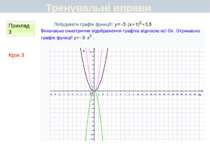
Пункт 3.4-3.5. Що є графіком функції у = а(х + т)2 + n. Графік функції у = -3(х - 2)2 + 1 можна побудувати, виконавши такі перетворення графіків: у = -3х2 у = -3(х - 2)2 у = -3(х - 2)2 + 1. У результаті отримаємо параболу виду у = -3х2 з координатами вершини (2; 1) і віссю симетрії х = 2. Отже, графік функції у = а(х + т)2 + n є параболою виду у = ах2, вершина якої має координати (—т; n), а віссю симетрії є пряма х= - т.

Тренувальні вправи Крок 1 Приклад 1

Тренувальні вправи Крок 2 Приклад 1

Тренувальні вправи Крок 3 Приклад 1

Тренувальні вправи Крок 4 Приклад 1

Тренувальні вправи Крок 1 Приклад 2

Тренувальні вправи Крок 2 Приклад 2

Тренувальні вправи Крок 3 Приклад 2

Тренувальні вправи Крок 4 Приклад 2

Тренувальні вправи Крок 1 Приклад 3

Тренувальні вправи Крок 2 Приклад 3

Тренувальні вправи Крок 3 Приклад 3

Тренувальні вправи Крок 4 Приклад 3

Тренувальні вправи Крок 5 Приклад 3

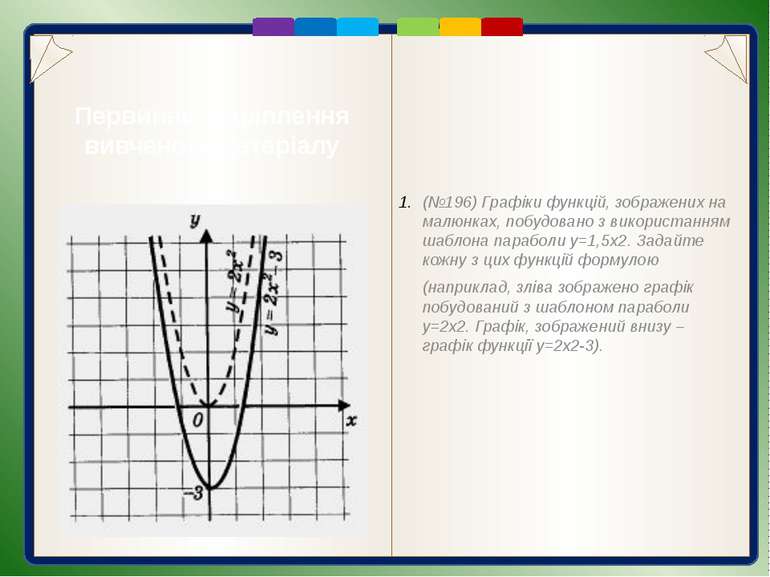
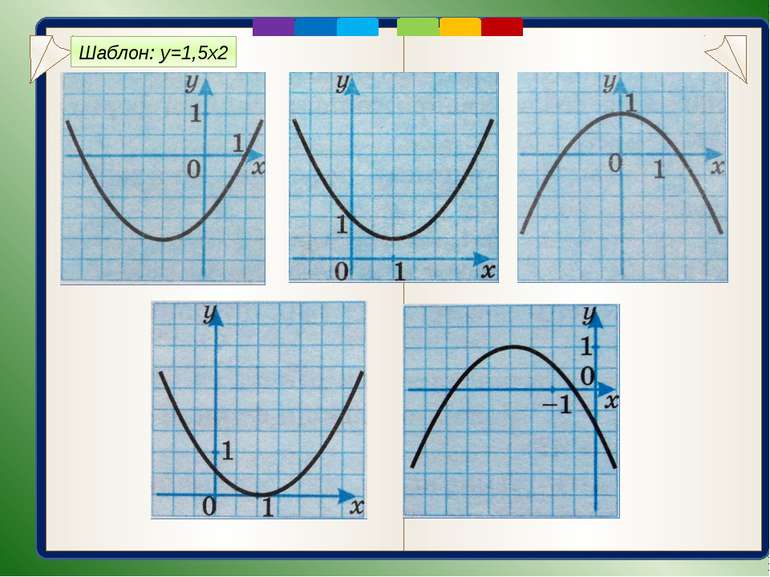
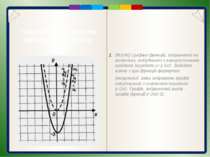
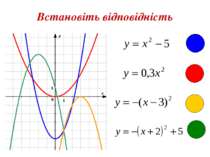
Первинне закріплення вивченого матеріалу (№196) Графіки функцій, зображених на малюнках, побудовано з використанням шаблона параболи у=1,5х2. Задайте кожну з цих функцій формулою (наприклад, зліва зображено графік побудований з шаблоном параболи у=2х2. Графік, зображений внизу – графік функції у=2х2-3).

Шаблон: у=1,5х2

Встановіть відповідність

Завдання для самоконтролю Який вигляд має графік функції у = а(х+т)2+т? Яка пара чисел позначає координати вершини параболи, що є графіком функції у = а(х+т)2+т: а) (т;n); б) (m; -n); в) (-т; n); г) (-т; -n)? 3. Як побудувати графік функції у = а(х+т)2+n?

Шаблон

Встановіть відповідність

Завдання для