Презентація на тему:
Диференціальне та інтегральне числення. Диференціальні рівняння.

Диференціальне та інтегральне числення. Диференціальні рівняння.

ПЛАН Похідна функції. Диференціал функції. Застосування диференціала. Функція багатьох змінних. Частинна похідна. Частинні і повний диференціали. Застосування повного диференціала. Невизначений інтеграл. Властивості невизначеного інтеграла. Визначений інтеграл. Формула Ньютона-Лейбніца. Властивості визначеного інтеграла. Основні поняття теорії диференціальних рівнянь.

Похідна та диференційованість функції Функція f має в точці x похідну: Фізичний зміст похідної: Геометричний зміст похідної: Функція f диференційована в точці x: Функція f неперервна в точці x Арифметичні операції над диференційованими функціями u I v: Похідна складеної функції y=f(u), u=ф(x): Похідна оберненої функції x=ф(y): Таблиця похідних Похідні вищого порядку:

В чому полягає суть фізичного та геометричного змісту похідної та як його використовувати в математичних задачах?

І.Ньютон сформулював дві основні проблеми математичного аналізу: 1). Довжина шляху, який долається, є постійною(тобто в будь-який момент часу); необхідно знайти швидкість руху у пропонований час; 2). Швидкість руху постійно дана; необхідно знайти довжину пройденого у запропонований час шляху.

1). Задача про миттєву швидкість: 2). Задача про знаходження змінного струму, який проходить по провіднику:

3). Друга похідна: (t)

4). Приклад:

Висновок:

N дотична січна M Дотичною до кривої в даній точці M, називається граничне положення січної MN, коли точка N прямує вздовж кривої до точкиM.

y x k-кутовий коефіцієнт рівняння дотичної до графіка функції в точці з абсцисою .

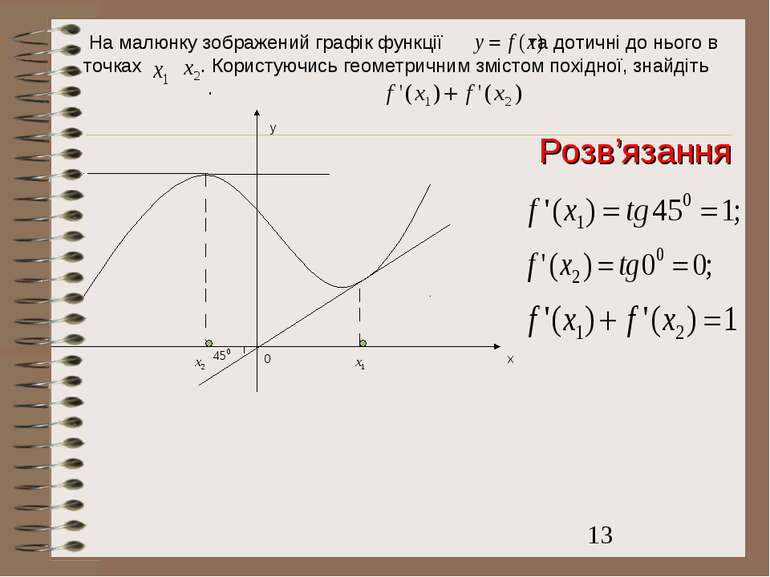
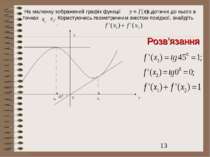
На малюнку зображений графік функції та дотичні до нього в точках . Користуючись геометричним змістом похідної, знайдіть . y x 0 Розв’язання

Знайдіть, при яких значеннях параметра а дотична до графіка функції у точці з абсцисою проходить через точку N(3;4). Розв’язання

Повне перетворення функції 2-х змінних Якщо обом змінним дати приріст, то функція отримає повне перетворення.

Означення фиференційованої функції. Функція називаєтся дифференційованою в точці М(х,у), якщо її повне перетворення можна представити у вигляді , де Δx и Δy -похідні аргументів х і у в де М(х,у), А і В –сталі, незалежні від Δx і Δy , -відстань між М(х,у) і

Означення диференціалу Головна лінійність відносно Δx и Δy частина повного перетворення функції називається повним диференціалом цієї функції і позначається dz або df(x,y) . Таким чином, .

Формула для обчислення дифференціала Якщо функція дифференційована в точці М(х,у),то вона має в цій точці частинні похідні , і причому =А, а =В . Таким чином, . Якщо , то

Диференціали вищих порядків Дифференціалом другого порядку функції z=f(x,y) називаєтся Вагалом: Якщо х і у незалежні зімінні, то

Достатня умова диференційованості функцій Нехай функція в деякому околі точки М(х,у) має частинні похідні, і , які неперервні в точці М. Тоді функція дифференційована в цій точці.

Достатня умова диференційованості функцій Озн. Функція, котра має в деякій точці неперервні частинні похідні, називається неперервно диференційованою в цій точці

Екстремуми функцій двох змінних Означення. Говорять, що в точці функція f (x,y) має максимум, якщо існує такий окіл цієї точки, що для всіх точок P(x,y) цього околу, відміннихх від , виконується нерівність Аналогічно визначається мінімум функції. Мінімум і максимум функції називаються її екстремумами. .

Екстремуми функцій двох змінних Теорема (необхідна умова екстремума). В точці екстремума функції декількох змінних кожна іі частинна похідна або рівна нулю, або не існує. Точки, в яких виконуються ці умови, називаются критичними.

Достатня умова екстремума функції двох змінних Теорема. Нехай функція z=f(x,y) визначена і має неперервні частинні похідні другого порядку в деякому околі точки , в якої . Якщо при цьому в цій точці виконується умова , то точка являється точкою екстремума функції, причому точкою максимума, якщо , і точкою мінімума, якщо . Якщо в цій точці , то екстремума в точці немає. У випадку, якщо в точке , теорема відповіді не дає.

Найбільше і найменше значення функції Означення. Найменше або найбільше значення функції в даній області називається абсолютним екстремумом функції (абсолютним мінімумом або абсолютним максимумом відповідно) в цій

Відповідно теоремі Вейєрштрасса неперервна в замкнутій області функція дясягає в ній свого найбільшого і найменшого значення. Абсолютний екстремум досягається функцією або в критичних точках, або га границі області.

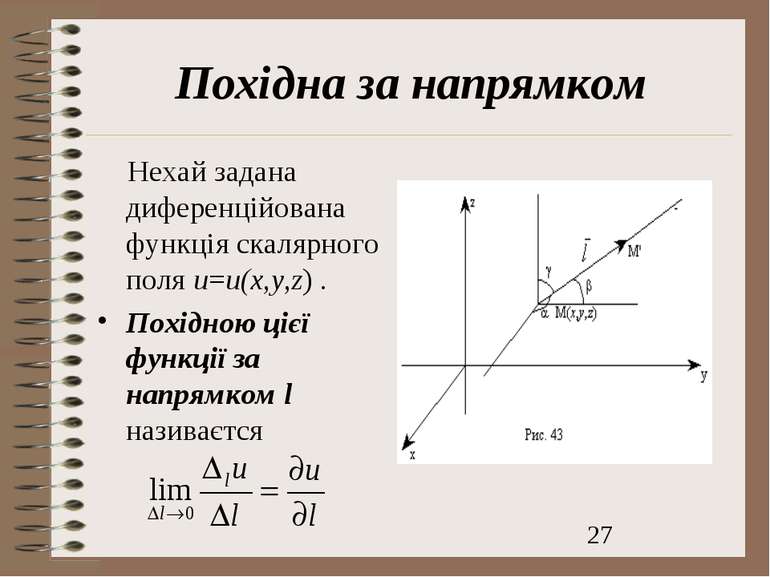
Похідна за напрямком Нехай задана диференційована функція скалярного поля u=u(x,y,z) . Похідною цієї функції за напрямком l називаєтся

Обчислення похідної за напрямком Похідну за напрямком обчислюють за формулою де cosα, cosβ , cosγ-напрямлюючі вектори. Для плоского скалярного поля

Градієнт скалярного поля Градієнтом скалярного поля u=u(x,y,z), де u=u(x,y,z)-дифференційована функція, називаєтся вектор з координатами . Таким чином, або .

Приклад: Найти градієнт функции u= в точці M(6,2,3). Розвязок . Обчислимо градієнт функції. Тоді grad u = + +

Напрямок градієнта Теорема. Похідна функції за напрямком рівна проекції градієнта цієї функції на даний напрямок (у відповідній точці).

Напрямок градієнта Так як похідна за напрямком представляє собою швидкість зміни функції в даному напрямку, а проекція вектора на інший вектор має максимальне значення, якщо оба вектори співпадають за напрямком, то градієнт функції в даній точці вказує напрямок найбільшого зростання функції.

Величина градієнта плоского скалярного поля Величина градієнта плоского скалярного поля: grad u = позначається tg і визначає кривизну найбільшого спуску або підйому поверхні u = f (x, y).

Продовження Градієнт скалярного поля в даній точці по величині і напрямку рівний максимальній швидкості зміни поля в цій точке, тобто. , де .

Напрямок градієнта Точка Р, в якої gradu(P)=0, називається явною точкою скалярного поля. У протилежному випадку цю точку називають неявною або звичайною точкою поля. Теорема. У всякій неявній точці плоского скалярного поля градієнт поля напрямлений по нормалі до лінії рівня, проходячи через цю точку, у сторону зростання поля

Інтегральне числення. Диференціальні рівняння.

Невизначений інтеграл, його властивості і обчислення Означення. Функція F(x) називається первісною функції f(x) на деякому проміжку, якщо для кожного х з цього проміжку Наприклад функція cosx являється первісною для функції – sinx, тому що

Первісна та невизначений інтеграл Очевидно, якщо F(x) – первісна функції f(x), то , де С –деяка постійна, також являється первісною для функції f(x). Якщо F(x) є будь – яка первісна для функції f(x), то всяка функція виду Ф(х)= також являється первісною для функції f(x)

Первісна та невизначений інтеграл Означення. Сукупність всіх первісних функції f(x),визначених на деякому проміжку, називається невизначеним інтегралом від функції f(x) на цьому проміжку і позначається

Первісна та невизначений інтеграл Якщо F(x) – деяка первісна для функції f(x), то пишуть = , хоча логічніше писати = . Ми по існуючих правилах будемо писати = . Таким чином один і той же символ буде визначати як всю сукупність первісних функції f(x), так і будь – який елемент цієї множини

Властивості інтеграла, котрі випливають з означення Первісна невизначеного інтегралу рівна підінтегральній функції, а його диференціал – його підінтегральному виразу. Тобто:

Властивості інтеграла, котрі випливають з означення Невизначений інтеграл від неперервно диференційованої функції дорівнює самій цій функції з точністю до постійної. Так як являється первісною для

Властивості інтегралу

Таблиця невизначених інтегралів

Таблиця невизначених інтегралів

Методи інтегрування Метод інтегрування заміни змінної. Метод інтегрування по частинах. Метод безпосереднього інтегрування

Метод інтегрування заміни змінної. Нехай потрібно знайти , причому безпосередньо підібрати первісну для ми не можемо, але нам відомо, що вона існує. Часто вдається найти первісну, ввівши нову змінну, по формулі: де , а - нова змінна

Метод інтегрування по частинах. Цей метод заснований на формулі:

Метод безпосереднього інтегрування Приклад. Обчислити

Визначений інтеграл. Означення. Вираз , де , називається інтегральною сумою функції на відрізку

Визначений інтеграл. Означення. Якщо існує , яка не залежить ні від способу розбиття відрізку на частини, ні від вибору точок , то така границя називається визначеним інтегралом функції на відрізку і позначається

Властивості визначеного інтегралу

Властивості визначеного інтегралу

Обчислення визначеного інтегралу Теорема. Нехай - первісна функції Тоді Цю формулу називають формулою Ньютона – Лейбніца, з якої випливає, що для обчислення визначеного інтегралу необхідно знайти первісну від підінтегральної функції.

Визначення диференціального рівняння Означення.

Диференціальні рівняння

Загальний розв'язок диференціяльного рівняння Означення. Загальним розв'язком диференціального рівняння називається функція, яка після підстановки у диференціальне рівняння перетворює його в тотожність.

Частковий розв'язок диференціального рівняння

Запишимо це рівняння у такому вигляді: Загальний розвязок має такий вигляд:

Диференціальні рівняння типу: Називається диференціальне рівняння з розділеними змінними. Загальний розв'язок такого рівняння знаходиться за допомогою методу інтегрування:

Диференціальні рівняння типу: Це рівняння можна привести до рівняння типу поділивши на отримуємо