Презентація на тему:
"Відстань між мимобіжними прямими"

Відстань між мимобіжними прямими  

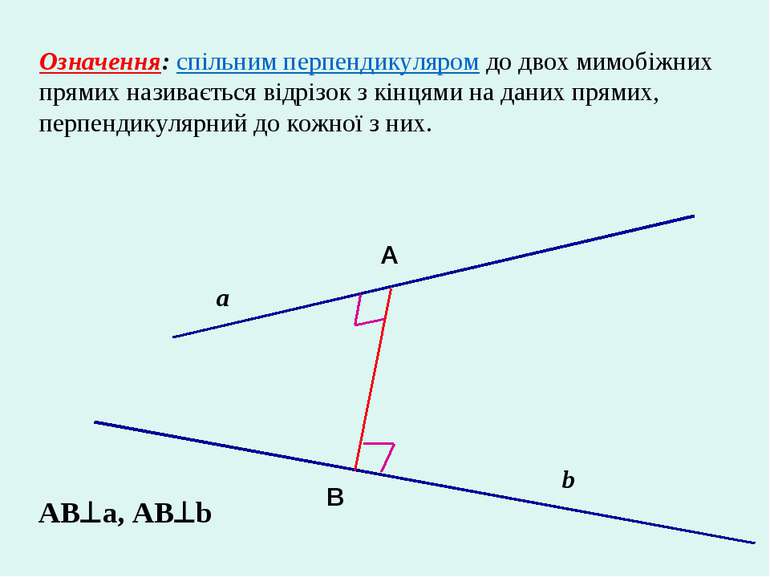
Означення: спільним перпендикуляром до двох мимобіжних прямих називається відрізок з кінцями на даних прямих, перпендикулярний до кожної з них. a b A B AB a, AB b

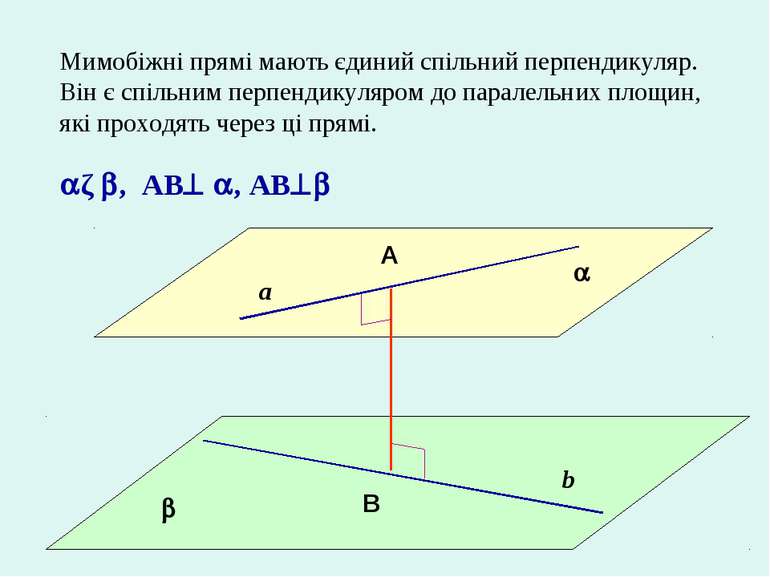
Мимобіжні прямі мають єдиний спільний перпендикуляр. Він є спільним перпендикуляром до паралельних площин, які проходять через ці прямі. a b A B ǁ , AB , AB

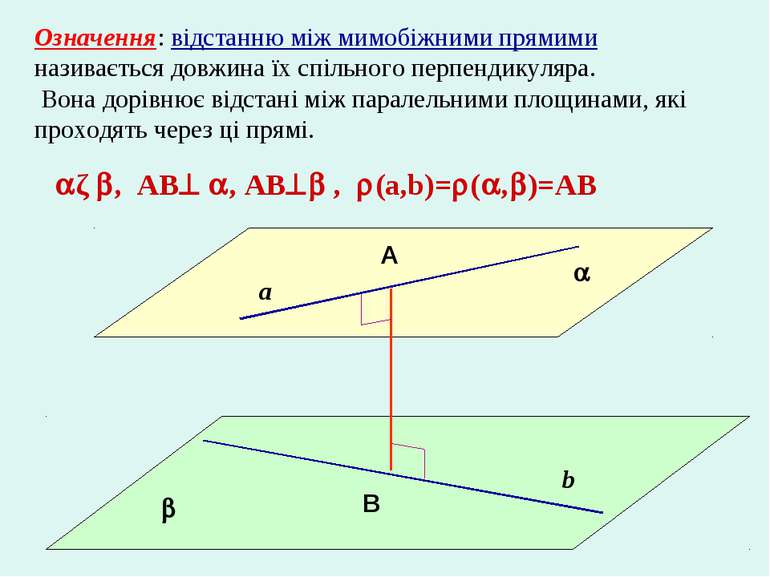
Означення: відстанню між мимобіжними прямими називається довжина їх спільного перпендикуляра. Вона дорівнює відстані між паралельними площинами, які проходять через ці прямі. a b A B ǁ , AB , AB , (a,b)= ( , )=AB

Основні способи знаходження відстані між двома мимобіжними прямими 1)Будують спільний перпендикуляр до даних мимобіжних прямих і обчислюють його довжину; 2) Проводять через дані мимобіжні прямі паралельні площини і обчислюють відстань між ними; 3) Проводять через одну з мимобіжних прямих площину, паралельну другій прямій і обчислюють відстань до цієї площини від паралельної до неї прямої; 4) Проводять площину, перпендикулярну до однієї з даних прямих і ортогонально проектують на неї обидві прямі. Шукана відстань дорівнює відстані між проекціями цих прямих.

Спосіб 1. Знаходження спільного перпендикуляра В ході розв’язання відшукують або будують спільний перпендикуляр до даних мимобіжних прямих і обчислюють його довжину Задача 1. Ребро куба дорівнює а. Знайти відстань між прямими ВC і DD1 CD BC, CD DD1 як суміжні сторони квадратів – граней куба CD – спільний перпендикуляр для прямих BC та DD1 (BC, DD1)=DC=a

Спосіб 1. Знаходження спільного перпендикуляра Задача 2. Ребро куба дорівнює а. Знайти відстань між прямими AA1 і CB1 AA1 A1B1 , BC BB1 , BB1 A1B1 як суміжні сторони квадратів – граней куба За теоремою про три перпендикуляри CB1 A1B1 A1B1 – спільний перпендикуляр для прямих B1C та AA1 (B1C, AA1)= A1B1 = a

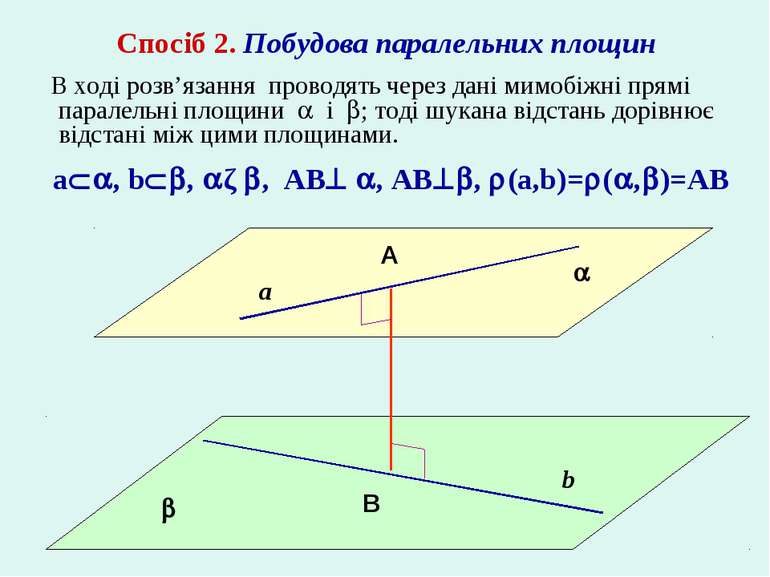
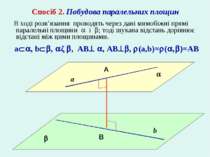
a b A B a , b , ǁ , AB , AB , (a,b)= ( , )=AB Спосіб 2. Побудова паралельних площин В ході розв’язання проводять через дані мимобіжні прямі паралельні площини і ; тоді шукана відстань дорівнює відстані між цими площинами.

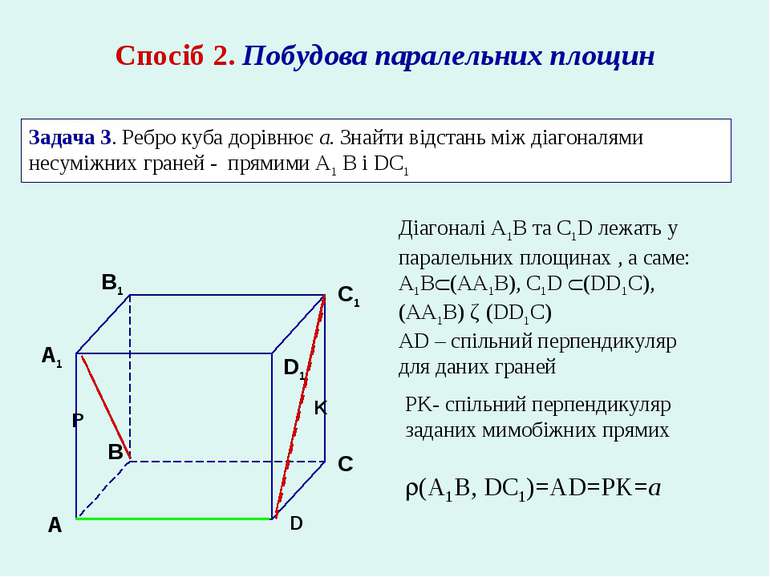
Спосіб 2. Побудова паралельних площин Задача 3. Ребро куба дорівнює а. Знайти відстань між діагоналями несуміжних граней - прямими A1 В і DC1 Діагоналі A1B та C1D лежать у паралельних площинах , а саме: A1B (AA1B), C1D (DD1C), (AA1B) ǁ (DD1C) AD – спільний перпендикуляр для даних граней P K PK- спільний перпендикуляр заданих мимобіжних прямих (A1B, DC1)=AD=PK=a

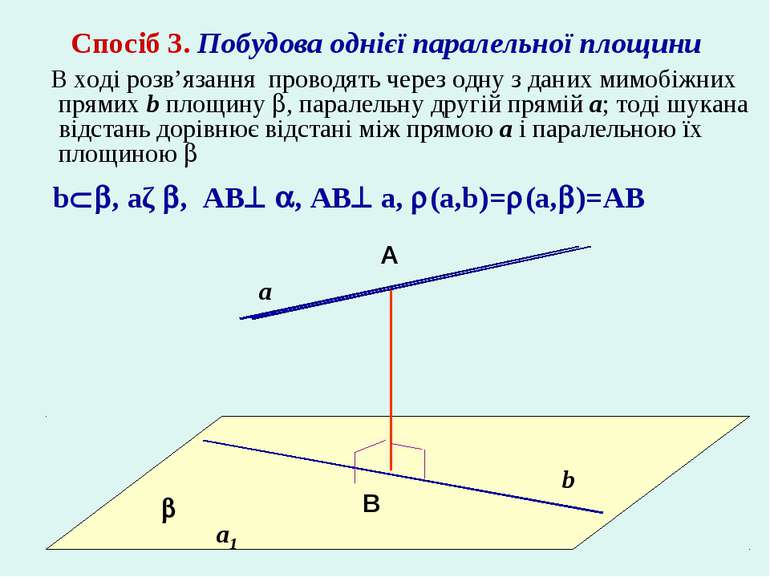
a b A B b , aǁ , AB , AB a, (a,b)= (a, )=AB Спосіб 3. Побудова однієї паралельної площини В ході розв’язання проводять через одну з даних мимобіжних прямих b площину , паралельну другій прямій a; тоді шукана відстань дорівнює відстані між прямою a і паралельною їх площиною a1

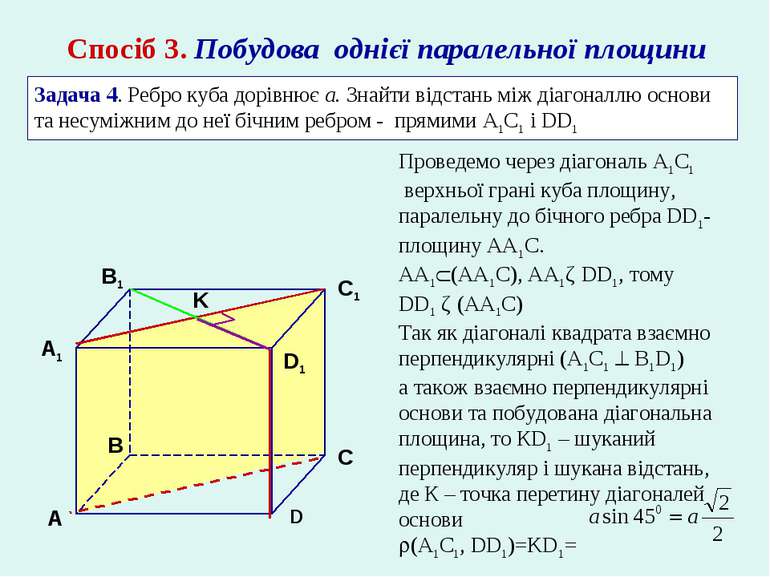
Спосіб 3. Побудова однієї паралельної площини Задача 4. Ребро куба дорівнює а. Знайти відстань між діагоналлю основи та несуміжним до неї бічним ребром - прямими A1С1 і DD1 Проведемо через діагональ A1C1 верхньої грані куба площину, паралельну до бічного ребра DD1- площину AA1C. AA1 (AA1C), AA1ǁ DD1, тому DD1 ǁ (AA1C) Так як діагоналі квадрата взаємно перпендикулярні (A1C1 B1D1) а також взаємно перпендикулярні основи та побудована діагональна площина, то КD1 – шуканий перпендикуляр і шукана відстань, де К – точка перетину діагоналей основи (A1С1, DD1)=KD1= K

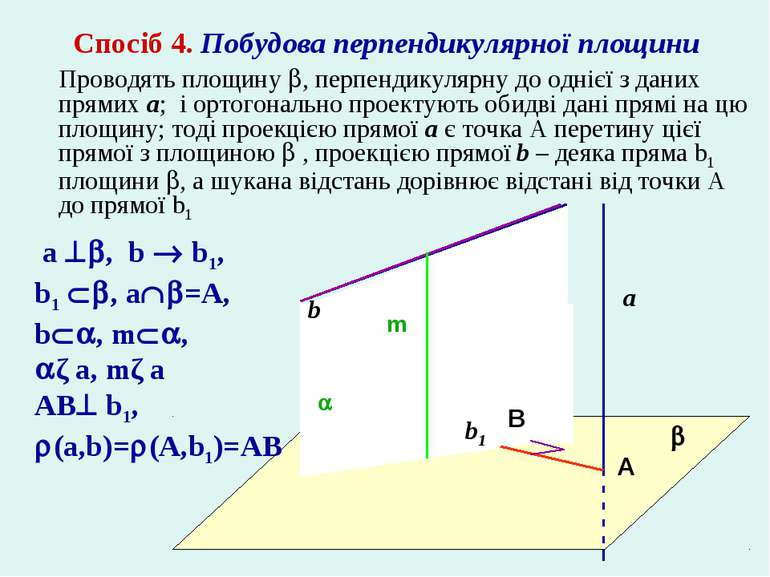
a b A B Спосіб 4. Побудова перпендикулярної площини Проводять площину , перпендикулярну до однієї з даних прямих a; і ортогонально проектують обидві дані прямі на цю площину; тоді проекцією прямої a є точка А перетину цієї прямої з площиною , проекцією прямої b – деяка пряма b1 площини , а шукана відстань дорівнює відстані від точки А до прямої b1 b1 m a , b b1, b1 , a =A, b , m , ǁa, mǁa AB b1, (a,b)= (A,b1)=AB

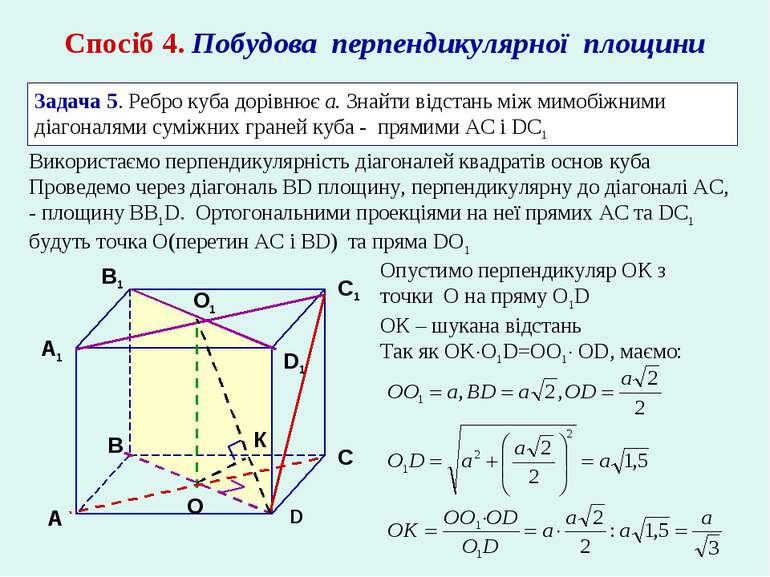
Спосіб 4. Побудова перпендикулярної площини Задача 5. Ребро куба дорівнює а. Знайти відстань між мимобіжними діагоналями суміжних граней куба - прямими AС і DС1 Опустимо перпендикуляр ОК з точки О на пряму О1D ОК – шукана відстань Так як OK O1D=OO1 OD, маємо: О1 О К Використаємо перпендикулярність діагоналей квадратів основ куба Проведемо через діагональ BD площину, перпендикулярну до діагоналі АС, - площину BB1D. Ортогональними проекціями на неї прямих AС та DC1 будуть точка О(перетин АС і BD) та пряма DO1

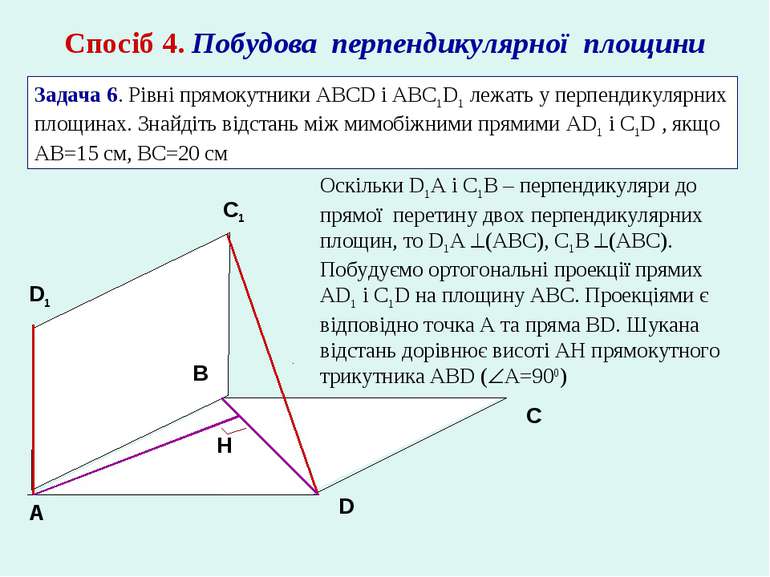
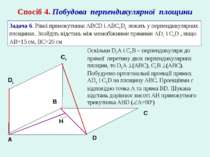
Спосіб 4. Побудова перпендикулярної площини Задача 6. Рівні прямокутники ABCD і ABC1D1 лежать у перпендикулярних площинах. Знайдіть відстань між мимобіжними прямими AD1 і С1D , якщо АВ=15 см, ВС=20 см C1 А B C D D1 H Оскільки D1A і C1В – перпендикуляри до прямої перетину двох перпендикулярних площин, то D1A (АВС), С1В (АВС). Побудуємо ортогональні проекції прямих AD1 і С1D на площину АВС. Проекціями є відповідно точка А та пряма BD. Шукана відстань дорівнює висоті АН прямокутного трикутника ABD ( A=900)

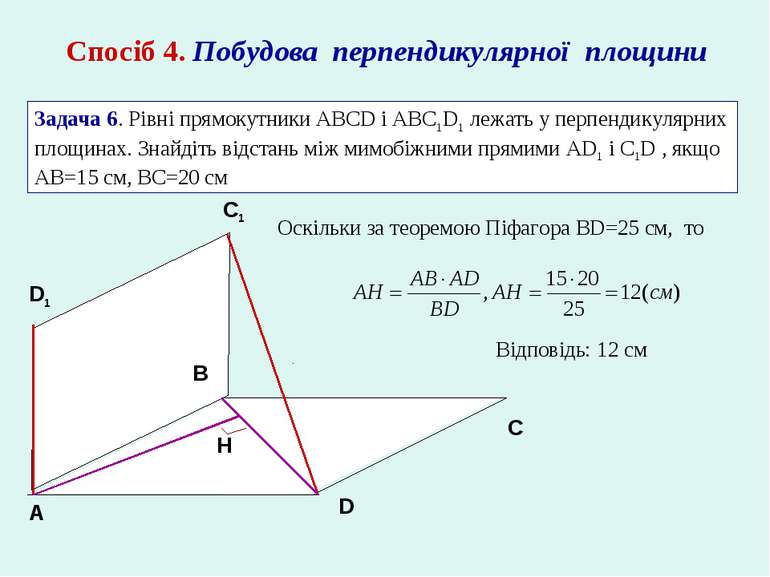
Спосіб 4. Побудова перпендикулярної площини Задача 6. Рівні прямокутники ABCD і ABC1D1 лежать у перпендикулярних площинах. Знайдіть відстань між мимобіжними прямими AD1 і С1D , якщо АВ=15 см, ВС=20 см C1 А B C D D1 H Оскільки за теоремою Піфагора ВD=25 см, то Відповідь: 12 см