Презентація на тему:
Велика теорема Ферма

Велика теорема Ферма Підготували: студентки гр. Б 3-1 Третяк Катя Сидоренко Анна LOGO

“Велика” або “Остання” теорема Ферма та її пояснення Великою теоремою Ферма називається той висновок, який було зроблено Фермою при читанні виданої Мезіріаком «Арифметики» Діофанту. На полях цієї книги, проти того місця, де йде мова про вирішення рівняння виду x2 + y2 = z2, він написав: «Тим часом, абсолютно неможливо розкласти повний куб на суму кубів, четвертую ступінь – на суму четвертих ступенів, взагалі який-небудь ступінь – на суму ступенів з тим же показником. Я знайшов справді дивовижний доказ цього припущення, але тут дуже мало місце, щоб його помістити». Це положення Ферма тепер формулюється як теорема в наступному вигляді: «Рівняння xn + yn = zn не може бути вирішене в раціональних числах відносно x, у і z при цілих значеннях показника n, великих 2».

Дослідники Справедливість цієї теореми підтверджується для багатьох окремих випадків (при цьому ще не знайдено жодного спростування), проте до цих пір вона не доведена в загальному вигляді, хоча їй цікавилися і її намагалися довести багато крупних математиків.

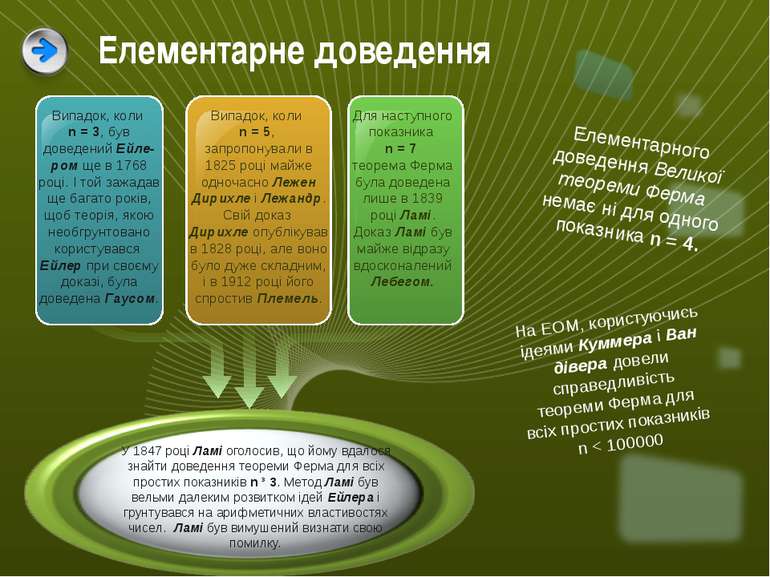
Елементарне доведення Елементарного доведення Великої теореми Ферма  немає ні для одного показника n = 4. Випадок, коли  n = 3, був доведений Ейле-ром ще в 1768 році. І той зажадав ще багато років, щоб теорія, якою необгрунтовано користувався  Ейлер при своєму доказі, була доведена Гаусом. Випадок, коли  n = 5, запропонували в 1825 році майже одночасно Лежен Дирихле і Лежандр. Свій доказ  Дирихле опублікував в 1828 році, але воно було дуже складним, і в 1912 році його спростив Племель. Для наступного показника  n = 7  теорема Ферма була доведена лише в 1839 році Ламі. Доказ Ламі був майже відразу вдосконаленийЛебегом. У 1847 році Ламі оголосив, що йому вдалося знайти доведення теореми Ферма для всіх простих показників n ³ 3. Метод Ламі був вельми далеким розвитком ідей Ейлера і грунтувався на арифметичних властивостях чисел.  Ламі був вимушений визнати свою помилку. На ЕОМ, користуючись ідеями Куммера і Вандівера довели справедливість теореми Ферма для всіх простих показників n < 100000

Доказ: Якщо розкласти cn на прості множники, то: cn = d1 *. * d1 * d2 *. * d2 *. * dm *. * dm, де кожного множника по n. Якщо ж розкласти на прості множники числа а і b, то якісь з чисел d1. dm підуть до а, якісь – до b, причому однакові піти і туди, і туди не можуть внаслідок того, що НОД (а; b)= 1, тобто а є твір n-х ступенів якихось простих чисел, і b також – твір n-х ступенів якихось чисел, отже: а = xn; b = yn Доказ Леми 1 (Жермен) Якщо твір два взаємно простих натуральних чисел є n-ой ступенем, то кожен із співмножників також буде  n-им ступенем: ab = cn; НОД (а; b)= 1; а, b Î N Довести:  а = xn; b = yn

x2 + y2 = z2 (1) Доказ Леми 2 (допоміжною) Якщо (x; у; z) – рішення, то (у; x; z) також буде рішенням, тому що x і у симетричні в даному рівнянні. Припустимо, що z = 2k, тоді z2 = 4k, якщо ж z = 2k – 1, то z2 = (2k – 1)2 = 4k2 – 4k + 1 = 4 (k2 – до)+ 1, отже, хоч би одне з чисел x і у парно, оскільки якби обидва вони були непарними, то x2 + y2 = (2k – 1) 2 + (2d – 1) 2 = 4k2 – 4k + 1 + 4d2 – 4d + 1 = 4 (k2 + d2 – до – d)+ 2, чого бути не може, оскільки x2 + y2 =z2. Крім того (x;± у; z) також є вирішенням рівняння, оскільки x2 = (-х) 2; y2 = (-у) 2; z2 = (-z) 2. З цих зауважень безпосередньо виходить, що нам досить знайти примітивні вирішення (x; у; z) рівняння (1), що лише складаються з позитивних чисел, тобто виключимо всі наступні рішення: (x±; у±; z), окрім (x; у; z), (у, x, z), для яких x = 2a

Лема 2 «Будь-яке примітивне вирішення (x, у, z) рівняння (1), що складається з позитивних чисел, для якого x = 2a, виражається формулами: x = 2mn; у = m2 – n2; z = m2 + n2 де n < m, НОД (m; n)= 1, m і n – числа різної парності» Доказ: Хай (x; у; z) – довільне примітивне вирішення рівняння (1), що складається з позитивних чисел, де x = 2a. З рівняння 4a2 + y2 = z2слідує (z – у) (z + у) = 4k2. Парність чисел z – у і z + у співпадають і твір їх рівне 4k2, отже, z – у і z + у парні. Хай z + у = 2b; z – у =2c, де b і з позитивні, оскільки у < z, виходячи з рівняння (1). Кожен загальний дільник lчисел b і з є також загальним дільником z = b + з і у= b – с НОД (у; z)= 1, оскільки (x; у; z) – примітивне вирішення рівняння (1), отже, НОД (b; з) = 1. З другого боку 4a2 = x2 = z2 – y2 = (z – у) (z + у) = 4bc, тобто a2 = bc. Отже, згідно лемі 1, застосованою до випадку, коли n = 2, існують такі взаємно прості позитивні числа різної парності m іn, що b = m2; з = n2. Тоді a2 = (mn) 2, тобто а = mn і x = 2a = 2mn; у = b – з = m2 – n2; z = b + з = m2 + n2 Для завершення доказу залишається лише додати, що n < m, оскільки x, у > 0

«x4 + y4 = z2    не має рішень в цілих відмінних від нуля числах» Доведення для показника 4 х4+y4=z4 Доказ: Припустимо, що існує вирішення рівняння (2) в цілих відмінних від нуля числах. Ясно, що, не втрачаючи спільності, ми можемо вважати, що воно складається з попарно взаємно простих позитивних чисел (якщо (x; у; z) є вирішенням рівняння (2), то, відразу ж видно, що (lx; lу; lz)також є його рішенням). Оскільки в будь-якій безлічі натуральних чисел існує найменше з них, то серед всіх таких рішень знайдеться рішення (x; у; z) з найменшим z. Розглянемо саме це рішення: Так само, як і при доказі леми 2 негайно доводиться, що одне з чисел x і у повинно бути парним. Припустимо, що парне число x. Це припущення також спільності не обмежує. Оскільки числа x2, y2 і z позитивні і взаємно прості, а число x2 парно, то, згідно лемі 2, існують такі взаємно прості числа m і n < m різної парності, що x2 = 2mn; y2 = m2 – n2; z2 = m2 + n2. Якщо m = 2k і n = 2f +1, то у = 4 (k2 – f2 – f – 1)+ 3, що неможливе, бо, як вище було вже відмічено, будь-який квадрат повинен мати вид 4k + 1, або 4k. Отже, m – непарно, а n – парно. Таким чином, припущення про існування у записаного вище рівняння (2) цілочисельних рішень приводить до суперечності. Отже, це рівняння не має рішень в цілих відмінних від нуля числах.

Примітки до доказів Теорема Ферма для показника 4 – це єдина теорема, доведена тут, оскільки доказ її вважається елементарним, тобто заснованим на простих перетвореннях алгебри чисел, відомим ще індусам. Доказ же цей був тут необхідний, оскільки ще навіть у Ферма воно було, тільки в декілька іншій формі. У Франції не так давно з'явилася книга, що є, ніби як, повним доведенням Великої теореми Ферма, але в ній використано стільки нових в математиці абстрактних понять, що перевірити ці праці, окрім автора, ніхто не може.

Дякуємо за увагу! LOGO