Презентація на тему:
Розв’язування алгебраїчних рівнянь вищих степенів методом заміни змінної

Урок з алгебри для 8 класу Тема: «Розв’язування алгебраїчних рівнянь вищих степенів методом заміни змінної»

Для поглибленого вивчення математики ФМГ №17 м. Вінниця 2012р. Автор: Дідик Валерія

Тема уроку: «Розв’язування алгебраїчних рівнянь вищих степенів методом заміни змінної» Мета уроку: - повторити функціональні методи розв’язування рівнянь; - розвивати вміння і навички розв’язування рівнянь різними методами.

Загальний підхід розв’язування рівнянь такого виду: Якщо в рівнянні (х+а)(х+b)(x+c)(x+d)=A і a+b=c+d, то виконуємо об’єднання співмножників (x2+(a+b)x+ab)(x2+(c+d)x+cd) 2. Виконуємо заміну: x2+(a+d)x=t 3.Далі рівняння зводиться до квадратного Розв’яжемо конкретний приклад:

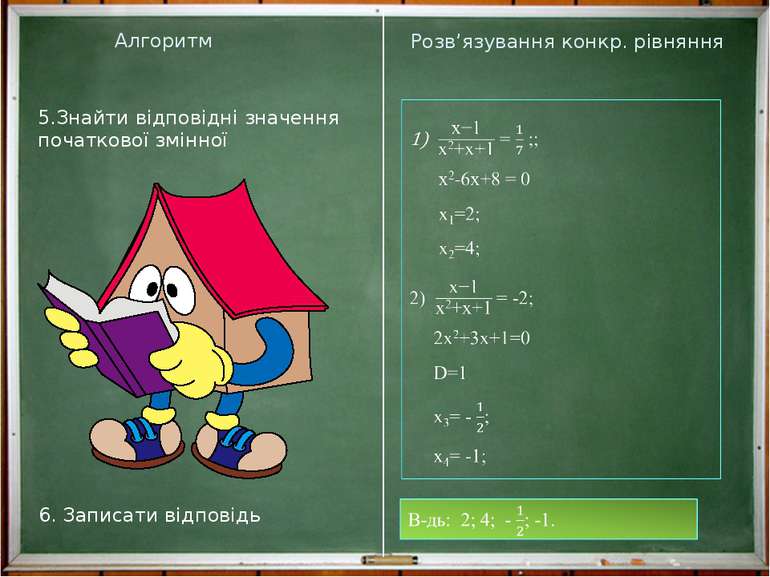
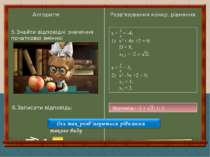
Алгоритм Розв’язування конкр. рівняння 1.Виконати групування по сумі вільних членів 2.Ввести заміну 3.Розв’язати нове рівняння відносно нової змінної 4.Знайти відповідні значення початкової змінної 5.Записати відповідь

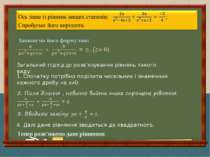
Спочатку запишемо його формулою: (х+а)(х+b)(x+c)(x+d)=Ax2 (a,b,c,d,A R) Загальний підхід до розв’язування рівнянь такого виду: Якщо в рівнянні (х+а)(х+b)(x+c)(x+d)=Ax2 і ab=cd, то виконуємо групуванн співмножників (x2+(a+b)x+ab)(x2+(c+d)x+cd)=Ax2 2. Ділимо обидві частини рівняння на х2 0 4.Далі рівняння зводиться до квадратного Тепер розв’яжемо дане рівняння:

Алгоритм Розв’язування конкр. рівняння 1.Перевірти чи х=0 не є коренем даного рівняння 576 0 2.Виконати групування по добутках вільних членів 3.Поділити обидві частини 4.Ввести заміну ((x+2)(x+12)((x+3)(x+8))=4x2; (x2+14x+24)(x2+11x+24)=4x2;

Алгоритм Розв’язування конкр. рівняння 7.Записати відповідь 6.Знайти відповідні значення початкової змінної (t+14)(t+11) = 4; t2+25t +154 = 0; t2+25t +150 = 0; t1 = -15; t2 = -10 5.Розв’язати отримане рівняння відносно нової змінної

Загальний підхід до розв’язування рівнянь такого виду: Рівняння такого виду називаються однорідними. 3. Далі дане рівняння зводиться до квадратного Тепер розв’яжемо даний приклад:

Алгоритм Розв’язування конкр. рівняння 1.Привести дане рівняння до загального вигляду 3. Ввести заміну 2(x2+x+1)2 – 7(x-1)2 = 13(x3-1) 2(x2+x+1)2 – 7(x-1)2 = 13(x-1)(x2+х+1) 4.Розв’язати отримане рівняння відносно нової змінної

6. Записати відповідь Алгоритм Розв’язування конкр. рівняння 5.Знайти відповідні значення початкової змінної

Спочатку запишемо його формулою: ax4+bx3+cx2+dx+e=0; (a,b,c,d R, e 0) Загальний підхід до розв’язування рівнянь такого виду: 2. Якщо умова виконується , то поділимо обидві частини рівняння на х2 0.

Алгоритм Розв’язування конкр. рівняння 2.Поділити обидві частини р-ня на x2 0. 3.Погрупувати доданки по степеням змінної х. 4.Ввести заміну.

Алгоритм Розв’язування конкр. рівняння t2+t-2- 4 = 0; t2+t – 6 = 0; t1= -3; t2= 2. 7.Записати відповідь: 6. Знайти відповідні значення початкової змінної. 5. Розв’язати отримане рівняння відносно нової змінної.

Загальний підхід до розв’язування рівнянь такого виду: 1. Спочатку потрібно поділити чисельник і знаменник кожного дробу на x 0. 4. Далі дане рівняння зводиться до квадратного. Тепер розв’яжемо дане рівняння:

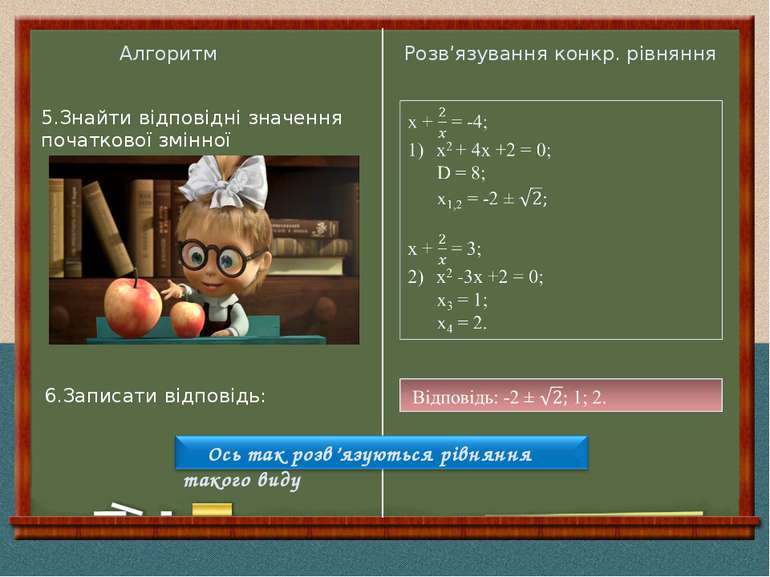
Алгоритм Розв’язування конкр. рівняння 1.Перевірти чи х=0 не є коренем даного рівняння. 2.Поділити чисельник і знаменник кожного дробу на х. 3. Ввести заміну. 4.Розв’язати отримане рівняння відносно нової змінної

Алгоритм Розв’язування конкр. рівняння 5.Знайти відповідні значення початкової змінної 6.Записати відповідь:

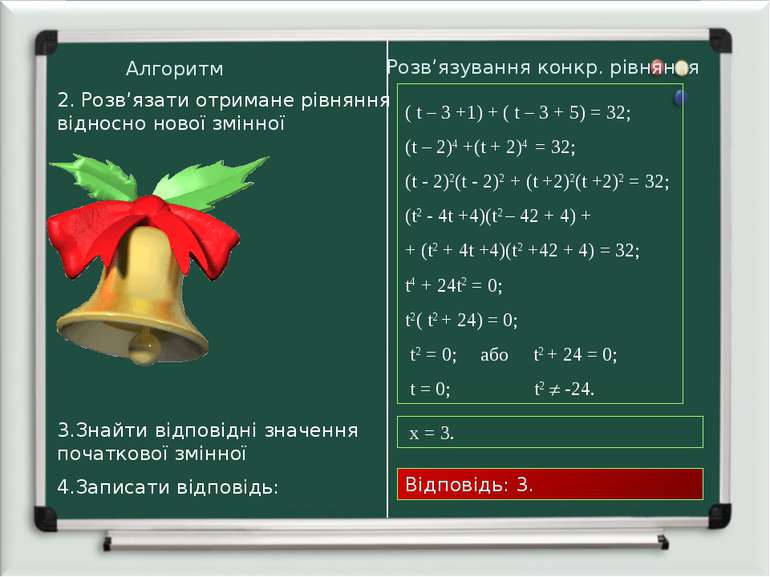
Загальний підхід до розв’язування рівнянь такого виду: Запишемо його формулою: ( ax + b1 )4 + (ax + b2 ) = 0, (a,b1,b2 R) 2. Далі рівняння такого типу зводяться до біквадратного. Алгоритм Розв’язування конкр. рівняння (x + 1)4 + (x + 5)4 = 32;

Алгоритм Розв’язування конкр. рівняння 2. Розв’язати отримане рівняння відносно нової змінної ( t – 3 +1) + ( t – 3 + 5) = 32; (t – 2)4 +(t + 2)4 = 32; (t - 2)2(t - 2)2 + (t +2)2(t +2)2 = 32; (t2 - 4t +4)(t2 – 42 + 4) + + (t2 + 4t +4)(t2 +42 + 4) = 32; t4 + 24t2 = 0; t2( t2 + 24) = 0; t2 = 0; або t2 + 24 = 0; t = 0; t2 -24. 3.Знайти відповідні значення початкової змінної x = 3. 4.Записати відповідь: Відповідь: 3.

Алгоритм Розв’язування конкр. рівняння 1. Виділити квадрат суми або різниці в лівій частині рівняння. 2. Ввести заміну. 3. Розв’язати отримане рівняння відносно нової змінної t2 = 40 – 18t; t2 +18t – 40 = 0; t1 = - 20; t2 = 2.

Алгоритм Розв’язування конкр. рівняння 4. Знайти відповідні значення початкової змінної 5. Записати відповідь:

Бажаю успіхів! Дідик Валерія.