Презентація на тему:
Проектна робота з теми: “ Зустріч з параметрами ”

Проектна робота з теми: “ Зустріч з параметрами ” Керівники проекту: Вчителі математики Комсомольської ЗОШ І-ІІІ ступенів №6. Вчитель вищої категорії звання “Старший учитель”Пазиненко С.В. і вчитель вищої категорії звання “Старший учитель” Єрмачкова В.О.

Мета проекту: Домогтися засвоєння учнями поняття “параметр” в різних видах задач; сформувати навички розв’язування задач з параметрами на різних етапах вивчення математики; розвивати творчу активність учнів, створювати умови для вияву ініціативи учнів під час вибору завдань; розвивати інтерес, творчі здібності та інтуїцію учнів, вміння застосовувати набуті знання в нових ситуаціях, виховувати зібраність, працьовитість, охайність, організованість, графічну та математичну культуру. виховувати в учнів прагнення до самовдосконалення, задоволення пізнавальних потреб, залучення учнів до позаурочної роботи.

Обладнання: Плакати із схемами; прикладами розв’язаних задач. Змістові питання: Знання методів дослідження лінійних та квадратних рівнянь. Уміння виділяти в задачах сталі та змінні величини та наводити у відповіді сімейство розв’язків відносно невідомої величини для всіх можливих значень сталих величин (параметрів). Навички роботи з навчальною, довідковою літературою; досвід роботи з комп’ютером.

Актуальність: Підготовка до державної підсумкової атестації як за курс основної ,так і за курс старшої школи а також зовнішнього незалежного оцінювання . Залучення учнів до дослідницької діяльності при вивченні математики. Розвиток навичок самостійної роботи з навчальною та довідковою літературою. Формування навичок нестандартного підходу до розв’язання проблемних завдань.

Навчальні предмети з якими пов’язаний проект: креслення, українська мова та література. Класи, яких стосується навчальний проект: 7, 9, 10. Термін, необхідний для реалізації навчального проекту: до завершення навчання в середній школі.

Державні освітні стандарти та навчальні програми Освітня галузь “Математика” Уміння розв’язувати лінійні, квадратні рівняння аналітичним та графічним способом. Уміння знаходити кількість коренів рівняння в залежності від значення параметра. Уміння будувати графіки функцій, що містять модуль та графіки рівняння з двома змінними. Застосування набутих знань при розв’язуванні задач з параметрами.

2. Освітня галузь “Технологія” Знання про проектний пошук як основу творчого процесу. Уміння здійснювати проектну діяльність за даними умовами. Давати творчу оцінку досконалості результатів проектної діяльності. 3. Освітня галузь “Українська мова та література” Формування комунікативності та літературної компетенції, що базується на знаннях, уміннях пізнавального і творчого типу, соціальних навичках, світоглядних переконаннях.

Навчальні цілі та очікувані результати навчання: Поглибити знання про задачі з параметрами, про дослідження лінійних та квадратних рівнянь. Практичне використання знань про рівняння при розв’язуванні задач з параметрами. Залучити учнів до використання дослідницьких методів під час вивчення курсу математики.

Учні під час проекту виробляють навички: Планування своєї навчальної діяльності, співпраці з однокласниками. Обговорення результатів науково-дослідницької діяльності та діяльності товаришів. Аналізу та систематизації одержаного матеріалу під час роботи над проектом.

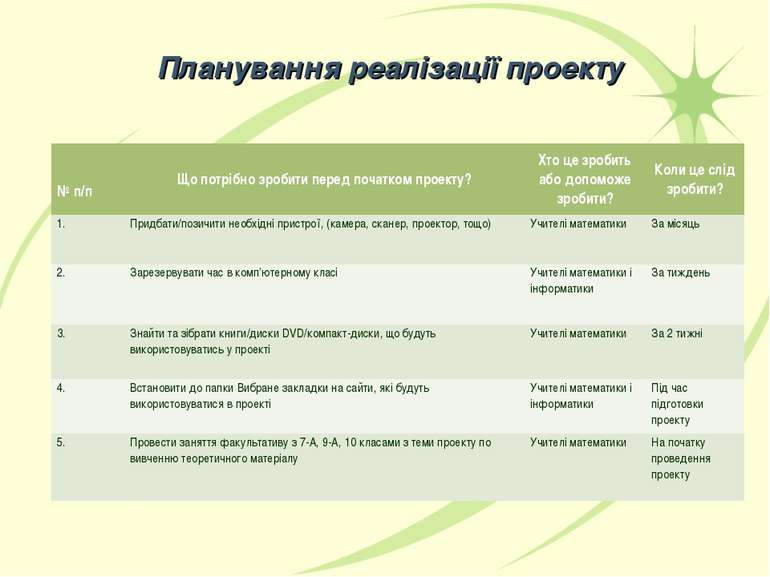
Планування реалізації проекту № п/п Що потрібно зробити перед початком проекту? Хто це зробить або допоможе зробити? Коли це слід зробити? 1.        Придбати/позичити необхідні пристрої, (камера, сканер, проектор, тощо) Учителі математики За місяць 2.        Зарезервувати час в комп’ютерному класі Учителі математики і інформатики За тиждень 3.        Знайти та зібрати книги/диски DVD/компакт-диски, що будуть використовуватись у проекті Учителі математики За 2 тижні 4.        Встановити до папки Вибране закладки на сайти, які будуть використовуватися в проекті Учителі математики і інформатики Під час підготовки проекту 5.        Провести заняття факультативу з 7-А, 9-А, 10 класами з теми проекту по вивченню теоретичного матеріалу Учителі математики На початку проведення проекту

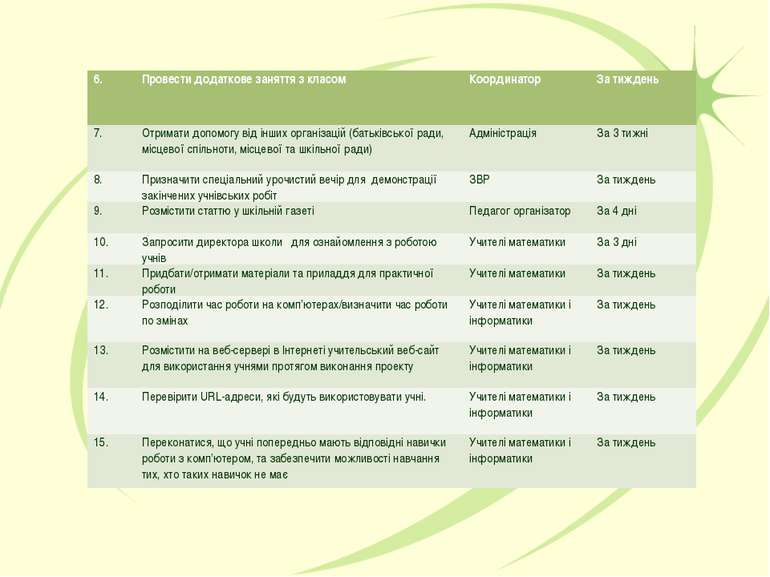
6.        Провести додаткове заняття з класом Координатор За тиждень 7.        Отримати допомогу від інших організацій (батьківської ради, місцевої спільноти, місцевої та шкільної ради) Адміністрація За 3 тижні 8.        Призначити спеціальний урочистий вечір для  демонстрації закінчених учнівських робіт ЗВР За тиждень 9.        Розмістити статтю у шкільній газеті Педагог організатор За 4 дні 10.    Запросити директора школи для ознайомлення з роботою учнів Учителі математики За 3 дні 11.    Придбати/отримати матеріали та приладдя для практичної роботи Учителі математики За тиждень 12.    Розподілити час роботи на комп’ютерах/визначити час роботи по змінах Учителі математики і інформатики За тиждень 13.    Розмістити на веб-сервері в Інтернеті учительський веб-сайт для використання учнями протягом виконання проекту Учителі математики і інформатики За тиждень 14.    Перевірити URL-адреси, які будуть використовувати учні. Учителі математики і інформатики За тиждень 15.    Переконатися, що учні попередньо мають відповідні навички роботи з комп’ютером, та забезпечити можливості навчання тих, хто таких навичок не має Учителі математики і інформатики За тиждень

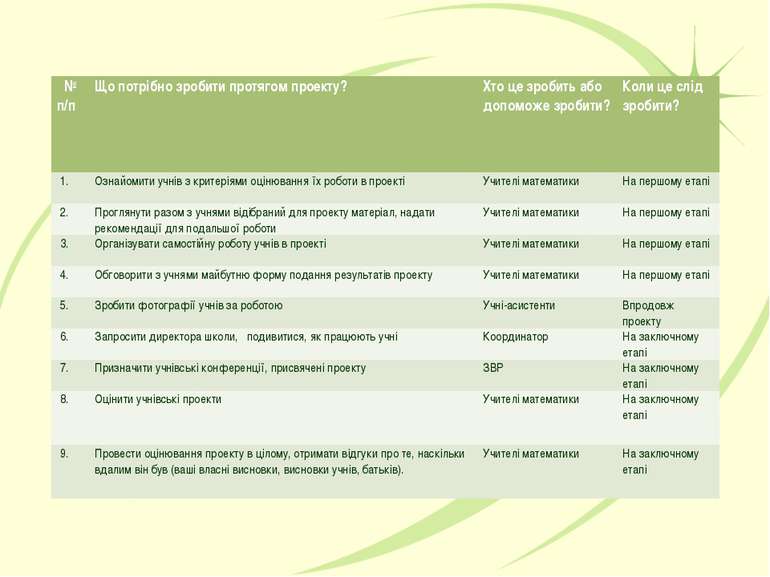
 № п/п Що потрібно зробити протягом проекту? Хто це зробить або допоможе зробити? Коли це слід зробити? 1.    Ознайомити учнів з критеріями оцінювання їх роботи в проекті Учителі математики На першому етапі 2.    Проглянути разом з учнями відібраний для проекту матеріал, надати рекомендації для подальшої роботи Учителі математики На першому етапі 3.    Організувати самостійну роботу учнів в проекті Учителі математики На першому етапі 4.    Обговорити з учнями майбутню форму подання результатів проекту Учителі математики На першому етапі 5.    Зробити фотографії учнів за роботою Учні-асистенти Впродовж проекту 6.    Запросити директора школи, подивитися, як працюють учні Координатор На заключному етапі 7.    Призначити учнівські конференції, присвячені проекту ЗВР На заключному етапі 8.    Оцінити учнівські проекти Учителі математики На заключному етапі 9.    Провести оцінювання проекту в цілому, отримати відгуки про те, наскільки вдалим він був (ваші власні висновки, висновки учнів, батьків). Учителі математики На заключному етапі

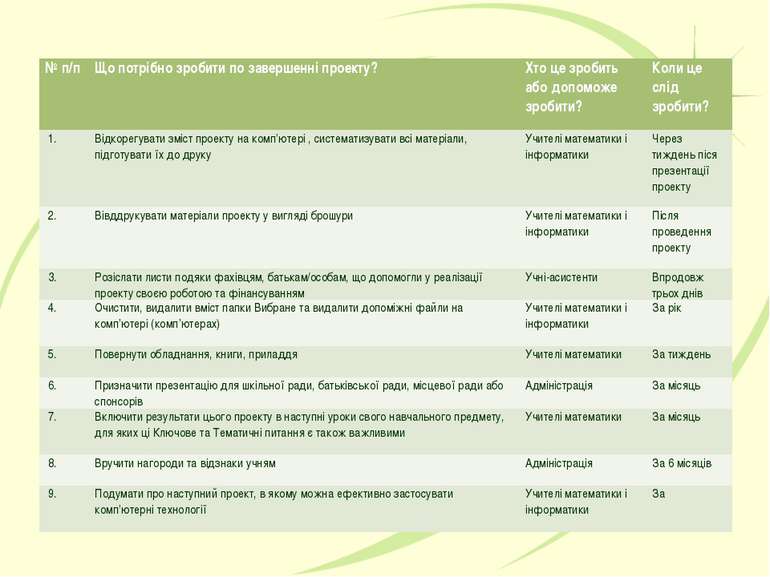
№ п/п Що потрібно зробити по завершенні проекту? Хто це зробить або допоможе зробити? Коли це слід зробити? 1. Відкорегувати зміст проекту на комп’ютері , систематизувати всі матеріали, підготувати їх до друку Учителі математики і інформатики Через тиждень піся презентації проекту 2. Вівддрукувати матеріали проекту у вигляді брошури Учителі математики і інформатики Після проведення проекту 3.    Розіслати листи подяки фахівцям, батькам/особам, що допомогли у реалізації проекту своєю роботою та фінансуванням Учні-асистенти Впродовж трьох днів 4.    Очистити, видалити вміст папки Вибране та видалити допоміжні файли на комп’ютері (комп’ютерах) Учителі математики і інформатики За рік 5.    Повернути обладнання, книги, приладдя Учителі математики За тиждень 6.    Призначити презентацію для шкільної ради, батьківської ради, місцевої ради або спонсорів Адміністрація За місяць 7.    Включити результати цього проекту в наступні уроки свого навчального предмету, для яких ці Ключове та Тематичні питання є також важливими Учителі математики За місяць 8.    Вручити нагороди та відзнаки учням Адміністрація За 6 місяців 9.    Подумати про наступний проект, в якому можна ефективно застосувати комп’ютерні технології Учителі математики і інформатики За 

Листок оцінювання Отримав Максимум Математика 10 Математична термінологія при поясненні. 10 Є пояснення до розв’язання, малюнків, схем. 10 Ключове запитання, показане на рівні знань учнів. 30 Усього з математики.

Отримав Максимум Зміст 5 Головна тема роботи, пов’язана з ключовими питаннями. 5 Матеріал подано у схемах, графіках. 5 Повідомлення виконані з використанням питань: що?, як?. 5 Список учасників роботи, хто яку роботу виконував? 20 Усього за зміст.

Отримав Максимум Оформлення 5 Усі публікації пов’язані з ключовим питанням. 5 Графіки, схеми, плакати використані ефективно, у належному форматі. 5 Тексти не мають граматичних та орфографічних помилок. 5 Зображення (графіки, плакати, схеми) збагачують презентацію. 20 Усього за оформлення.

Діяльність учнів та етапи проведення проекту На І етапі відбувається презентація теми майбутнього проекту, обговорюються основні аспекти її реалізаціі, а саме: формують три групи за віком і інтересами 7-А класу, 9-А класу, 10 класу; обумовлюються теми робіт кожної групи, джерела інформації, об’єми робіт.

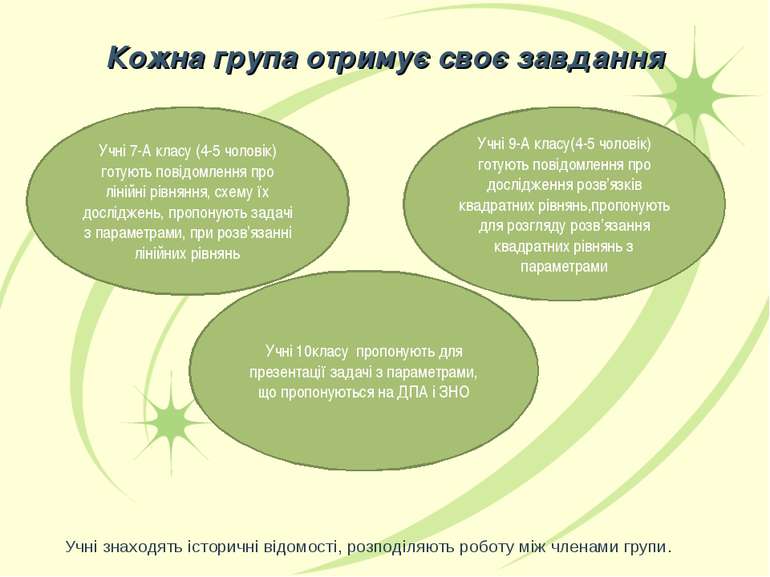
Кожна група отримує своє завдання Учні 7-А класу (4-5 чоловік) готують повідомлення про лінійні рівняння, схему їх досліджень, пропонують задачі з параметрами, при розв’язанні лінійних рівнянь Учні 9-А класу(4-5 чоловік) готують повідомлення про дослідження розв’язків квадратних рівнянь,пропонують для розгляду розв’язання квадратних рівнянь з параметрами Учні 10класу пропонують для презентації задачі з параметрами, що пропонуються на ДПА і ЗНО Учні знаходять історичні відомості, розподіляють роботу між членами групи.

На ІІ етапі учні працюють в групах над джерелами інформації для розкриття своєї теми, роблять повідомлення на заняттях факультативу, обговорюють проблемні питання. На цьому етапі вчителі проводять консультації з учнями щодо доцільності інформації. На ІІІ етапі проводиться оформлення матеріалів, узагальнення одержаних фактів у вигляді схем, плакатів, графіків. У групах обговорюються результати роботи кожного члена групи, на заняттях факультативу проводиться презентація дослідницької роботи кожної групи. На засіданні клубу “Тріада” презентуються результати роботи над проектом. Кожна група презентує свою роботу; показує, які знання вони одержали під час роботи над проектом.

Приклади учнівських презентацій Презентація І групи 7-А клас: Розв’язування рівнянь з параметрами визначається залежно від допустимих значень параметрів. Розв’язати рівняння з параметрами означає знайти всі його розв’язки для кожної системи допустимих значень параметрів. При розв’язуванні рівнянь з параметрами область зміни параметрів може бути заданою Якщо не вказані межі зміни параметрів, то вважається, що параметри набувають усіх своїх допустимих значень.

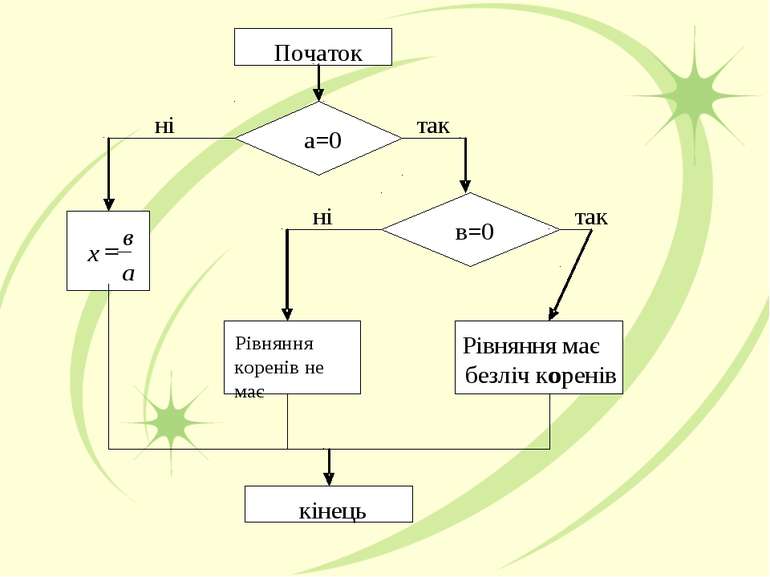
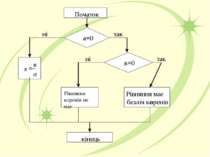
Для розв’язування рівнянь з параметрами слід користуватись розв’язуванням найпростішого лінійного рівняння ах =b: 1) якщо а ≠0, то при будь – якому значенні b рівняння ах =b має єдиний корінь х = b/a; 2) якщо а =0, b ≠0, то рівняння ах =b коренів не має; 3) якщо а =0 і b =0, то рівняння ах =b має безліч коренів. Цей висновок можна проілюструвати за допомогою блок – схеми.  

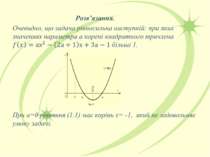
Приклад 1. Розв’язати рівняння ах -3 = b залежно від параметрів а і b. Розв’язання.   Виконавши у рівняння ах-3 = b тотожні перетворення, дістанемо: ах = b+3. якщо а≠0, то х = b+3/a при будь – якому b; якщо а =0, то при b= -3 рівняння набуває вигляду 0х=0, тобто коренями рівняння є всі числа; якщо а=0 і b≠-3, дістанемо 0х = b +3 ≠0, така рівність неможлива, тому рівняння коренів не має. Відповідь. при а ≠0 і будь – якому b х = b+3/a ; при а =0 і b = -3 корені рівняння – всі числа; при а=0 і b≠0 коренів немає.

Приклад 2. Розв’язати рівняння: ах=1 . Розв’язання. На перший погляд відповідь очевидна: х=1/а . Однак при а=0 дане рівняння немає розв’язків. Відповідь. Якщо а=0, то розв’язків немає; якщо а≠0, то х=1/а. Приклад 2. Розв’язати рівняння: х-3=а+1. Розв’язання. Перетворимо спочатку рівняння х=а+4. Рівняння має єдиний розв’язок незалежно від значення параметра а. Наприклад, якщо а=1,то х=5; а=0,то х=4; а=-4,то х=0. Зауважимо,що параметр а може набувати будь-яких значень, а значення х знаходимо за формулою х=а+4. Відповідь. х=а+4 для будь-якого значення параметра а.

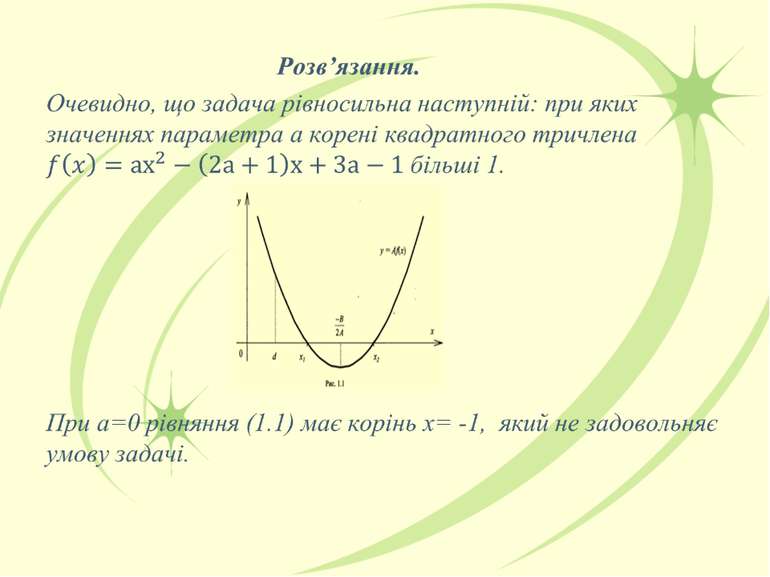
Презентація ІІ групи 9-А кллас: Нехай y=A(а)x2+B(а)x+C(а) - квадратний тричлен, коефіцієнти якого залежать від параметра а; D=B2-4AC – дискримінант цього рівняння; х_0=-В/2А - абсциса вершини параболи; y_0=-D/4А - ордината вершини параболи; y(α)=f(α)=Aα2+Bα+C- значення квадратного тричлена при х= α. Сформулюємо такі основні задачі: Розв’язати рівняння A(а) x2+B(а)x+C(а)=0 (А1). Розв’язати одну з нерівностей або їх систему. Знайти всі значення а, за яких рівняння має дійсні корені, і визначити їх знаки Дослідити розташування дійсних коренів рівняння (А1) відносно заданої точки чи проміжку

5) Знайти всі значення параметра а,за яких з однієї нерівності випливає інша 6) Визначити всі значення а, за яких корені рівняння (А1) задовольняють задану умову 7) Знайти всі значення параметра а, за яких рівняння А_1 (а) x2+В_1 (а)x+С_1 (а)=0 та А_2 (а) x2+В_2 (а)x+С_2 (а)=0 мають спільні корені (або хоча б один спільний корінь) 8) Знайти всі значення а, за яких квадратний тричлен y=A(а)x2+B(а)x+C(а) чи задана функція Р(х1:х2), де х1,х2- дійсні корені рівняння (А1), набуває найбільшого (найменшого) значення на заданому проміжку. Розв’язування квадратного рівняння з коефіцієнтами, залежними від параметра: A(а) x2+B(а)x+C(а)=0 (1)

Презентація ІІІ групи 10клас: При підготовці до державної підсумкової атестації у 9 та 11 класі, до зовнішнього незалежного оцінювання та до математичних олімпіад у 10 класі ми розв’язуємо задачі з параметрами на відшукання кількості розв’язків рівняння з двома змінними, систем рівнянь з двома змінними.

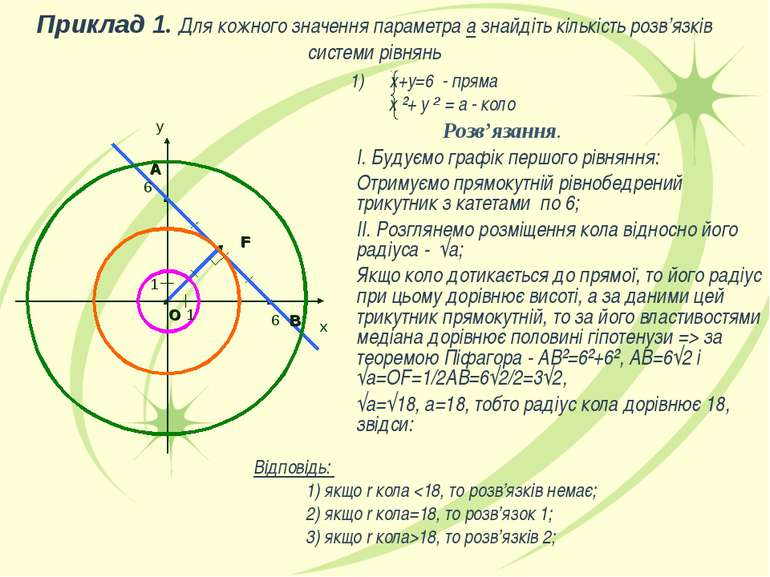
. . . у 1) х+у=6 - пряма х ²+ у ² = а - коло Відповідь: 1) якщо r кола 18, то розв’язків 2; Приклад 1. Для кожного значення параметра а знайдіть кількість розв’язків системи рівнянь Розв’язання. І. Будуємо графік першого рівняння: Отримуємо прямокутній рівнобедрений трикутник з катетами по 6; ІІ. Розглянемо розміщення кола відносно його радіуса - √а; Якщо коло дотикається до прямої, то його радіус при цьому дорівнює висоті, а за даними цей трикутник прямокутній, то за його властивостями медіана дорівнює половині гіпотенузи => за теоремою Піфагора - АВ²=6²+6², АВ=6√2 і √а=OF=1/2АВ=6√2/2=3√2, √а=√18, а=18, тобто радіус кола дорівнює 18, звідси:

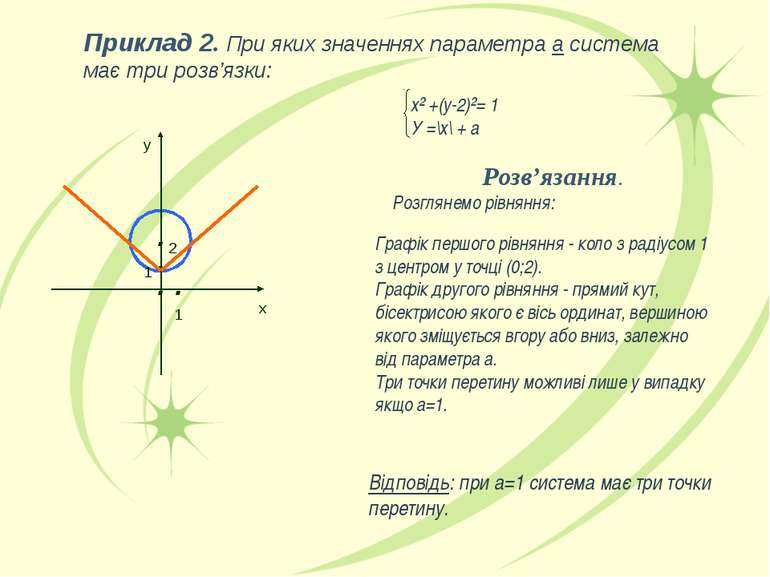
Приклад 2. При яких значеннях параметра а система має три розв’язки: х² +(у-2)²= 1 У =\х\ + а Розв’язання. Розглянемо рівняння: Графік першого рівняння - коло з радіусом 1 з центром у точці (0;2). Графік другого рівняння - прямий кут, бісектрисою якого є вісь ординат, вершиною якого зміщується вгору або вниз, залежно від параметра а. Три точки перетину можливі лише у випадку якщо а=1. Відповідь: при а=1 система має три точки перетину. . . .

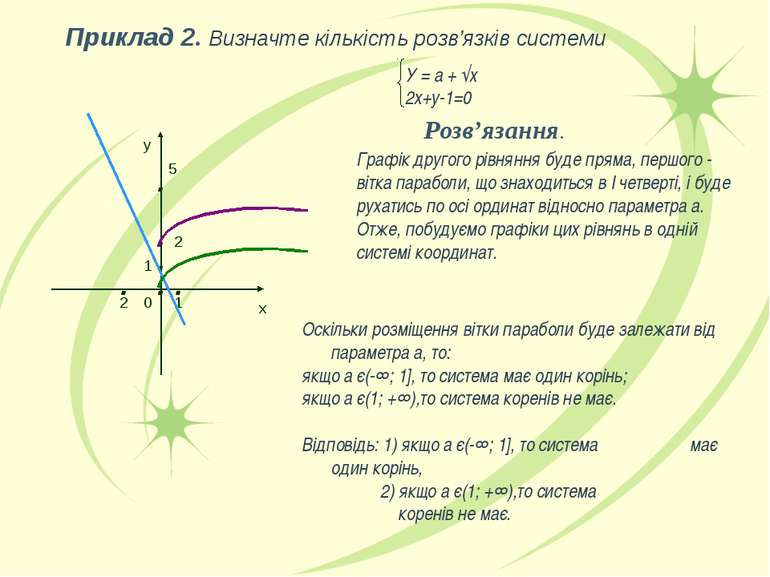
У = а + √х 2х+у-1=0 Розв’язання. Графік другого рівняння буде пряма, першого - вітка параболи, що знаходиться в І четверті, і буде рухатись по осі ординат відносно параметра а. Отже, побудуємо графіки цих рівнянь в одній системі координат. Оскільки розміщення вітки параболи буде залежати від параметра а, то: якщо а є(-∞; 1], то система має один корінь; якщо а є(1; +∞),то система коренів не має. Відповідь: 1) якщо а є(-∞; 1], то система має один корінь, 2) якщо а є(1; +∞),то система коренів не має. . . . . 1 у . 0 Приклад 2. Визначте кількість розв’язків системи

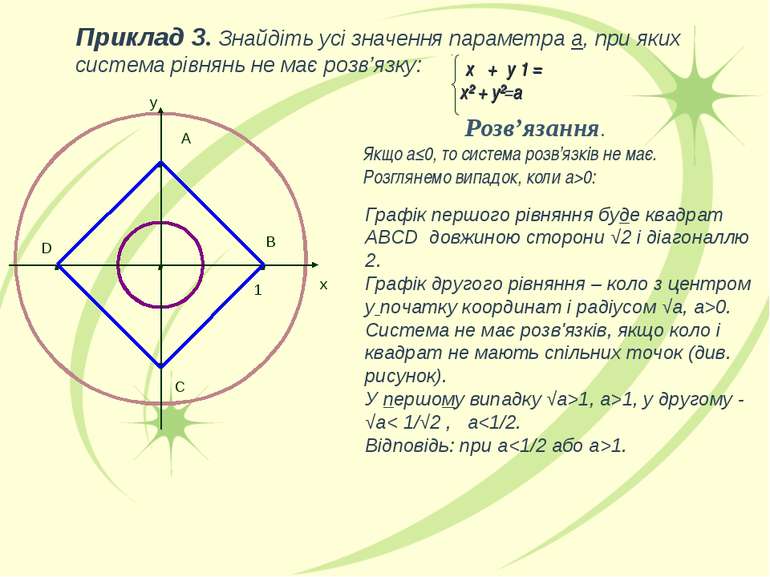
Приклад 3. Знайдіть усі значення параметра а, при яких система рівнянь не має розв’язку: . . . . . B ׀х ׀ + ׀у ׀= 1 х² + у²=а Розв’язання. Якщо а≤0, то система розв’язків не має. Розглянемо випадок, коли а>0: Графік першого рівняння буде квадрат ABCD довжиною сторони √2 і діагоналлю 2. Графік другого рівняння – коло з центром у початку координат і радіусом √а, а>0. Система не має розв'язків, якщо коло і квадрат не мають спільних точок (див. рисунок). У першому випадку √а>1, а>1, у другому - √а< 1/√2 , а

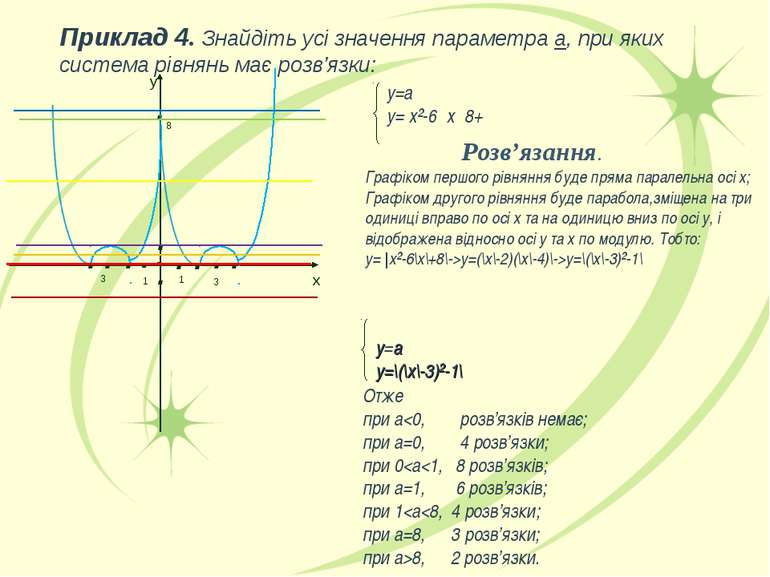
. . . у=а у=׀х²-6 ׀х׀+8 ׀ Розв’язання. Графіком першого рівняння буде пряма паралельна осі х; Графіком другого рівняння буде парабола,зміщена на три одиниці вправо по осі х та на одиницю вниз по осі у, і відображена відносно осі у та х по модулю. Тобто: у= |x²-6\х\+8\->у=(\x\-2)(\x\-4)\->y=\(\x\-3)²-1\ Отже при а

Відповідь: 1) при а

А тепер ми хочемо дізнатись вашу думку про проект. Як змінились ваші знання про задачі з параметрами? Розвитку яких рис характеру сприяв проект (самостійності, відповідальності, працелюбності)? Які пізнавальні процеси були задіяні під час проекту найбільше (мислення, пам’ять, уява, увага)? Якого життєвого досвіду ви набули (володіти собою, захищати свої знання, бути впевниними в собі)? Чи отримали ви задоволення від власної праці?

Дякуємо за увагу!