Презентація на тему:
Презентація творчого проектуКушнір Світлани Іванівни

Презентація творчого проекту Кушнір Світлани Іванівни вчителя математики Вінницького технічного ліцею

Швидка допомога учням по темі “Нерівності”

І. Т е с т на знання теоретичної основи теми

1. Які види нерівностей вам відомі? 2. Які знаки нерівностей відповідають кожному з типу нерівностей? 3. Як у кожному з випадків при зображенні розв'язків нерівності на координатній прямій зображається точка? 4. Які дужки використовують у кожному з випадків при запису відповіді у вигляді проміжку? 5. Яка дужка ставиться біля знака нескінченності? 6. Порівняйте числа a і b, якщо: а) різниця a – b = –12; б) різниця a – b = 20. 7. Назвіть цілі числа, які належать числовому проміжку: а) [-1; 2]; б) (3,5; 6). 8. При яких значеннях а правильна нерівність: а) б)

Відповіді: 1 Строгі нерівності Нестрогі нерівності 2 < > ≤ ≥ 3 ○ ● 4 ( ) [ ] 5 ( ∞ ) 6 a < b a > b 7 -1; 0; 1; 2 4; 5 8 при a > – 8 при a > 3

А Ви прочитайте! Листок-вкладиш. Інформація для пацієнта (учня). ІІ. Методи розв’язування нерівностей Він [Гена] дуже любив читати точні та серйозні книги: довідники, підручники або розклади руху потягів. Успенський Е.Н. Крокодил Гена та його друзі.

Прочитайте уважно цей листок-вкладиш перед тим, як розпочати застосування препарату! Законспектуйте цей листок-вкладиш. Вам може знадобитися перечитати його. Якщо у Вас виникнуть додаткові запитання, будь ласка, проконсультуйтеся з Вашим лікарем (вчителем). Цей препарат призначений не тільки Вам, тому можна передавати його іншим особам, які хворіють нерівностями. Це ні в якому разі не може зашкодити їхньому математичному здоров’ю, навіть якщо симптоми їхнього захворювання подібні до тих, які спостерігаються у Вас.

Склад лікарського засобу: лінійні нерівності, нерівності другого степеня, системи лінійних нерівностей, нерівності з модулем, дробові раціональні нерівності. Лікарська форма. Алгоритми. Показання. Бажання вміти розв’язувати нерівності. Протипоказання. НЕМАЄ. Спосіб застосування. Препарат слід приймати перед виконанням домашнього завдання, при підготовці до самостійної, контрольної роботи, ДПА, ЗНО тощо. Дози. Препарат слід приймати протягом будь-якого часу та в будь-яких ефективних дозах. Побічні ефекти. У випадку виникнення будь-яких незвичних реакцій негайно порадьтеся з вчителем щодо подальшого застосування препарату.

Таблиця 2

Таблиця 3

Таблиця 4 Нерівності з модулем │f (x)│< a (≤) [a>0] Алгоритм розв’язування Перехід до системи нерівностей 2. Розв’язати систему. 3. Відповідь

Таблиця 5 Нерівності з модулем │f (x)│> a (≥) [a>0] Алгоритм розв’язування Перехід до сукупності нерівностей 2. Розв’язати сукупність. 3. Відповідь

Таблиця 6

Методична вказівка до методу інтервалів. Корисно знати правило зміни знаку дробово-раціональної функції: якщо число х0 зустрічається у списку всіх нулів чисельника і знаменника дробу парну кількість раз, то при переході через точку х0 функція не змінює знак, якщо непарну – то змінює на протилежний. Для відповіді вибираємо інтервали з певним знаком ( у відповідності зі знаком нерівності)

ІІІ. „Препарат в дії” А тепер спробуйте на практиці порівняти наведені методи і з’ясувати найбільш універсальний для цієї групи нерівностей. Для того, щоб Ваше остаточне рішення було максимально об’єктивним, після розв’язання кожної із запропонованих нерівностей необхідно заповнити таблицю 7 знаками + чи – .

Який можна зробити висновок? Таблиця 7 Нерівності Лінійні нерівності (графічний метод) Системи лінійних нерівностей Метод інтервалів 1 2 х – 8 > 0 2 х2 – 4х – 5 < 0 3 (х + 4) (х – 7) ≥ 0 4 5 х3 – 4х ≥ 0 6 (х2 – 5х + 6) (5– х) ≤ 0 7 │7х +3│< 13 Разом

ІV. Усна розминка (Розв’язування тестових завдань) Дуже часто у житті нам приходиться робити вибір. І як важливо, щоб він був правильним. А вихід завжди є ! Цей нещасний хлопець один варіант уже використав , стріла не допомогла, а йому пропонують тільки два – рогатку і сачок і жоден з них не підходить. А Вам пропонують чотири варіанти відповідей в тестових завданнях і серед них обов’язково є лише одна правильна.

V. „Вчимося на чужих помилках” Порада вчитися на помилках інших безглузда. Навчитися чогось можна тільки на власних. Бернард Шоу

В цьому розділі Вам пропонують попрацювати в ролі вчителя. Ваше завдання – знайти помилку в наведених неправильних розв’язаннях нерівностей, а це, найчастіше буває важче, ніж просто розв’язати нерівність.

Эту задачу Штирлиц решал уже в шестой раз. Он ненавидел эту задачу. Ответ опять не совпал. По Ю.Семенову VІ. „Відгадай слово” (Самостійна робота)

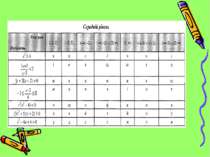
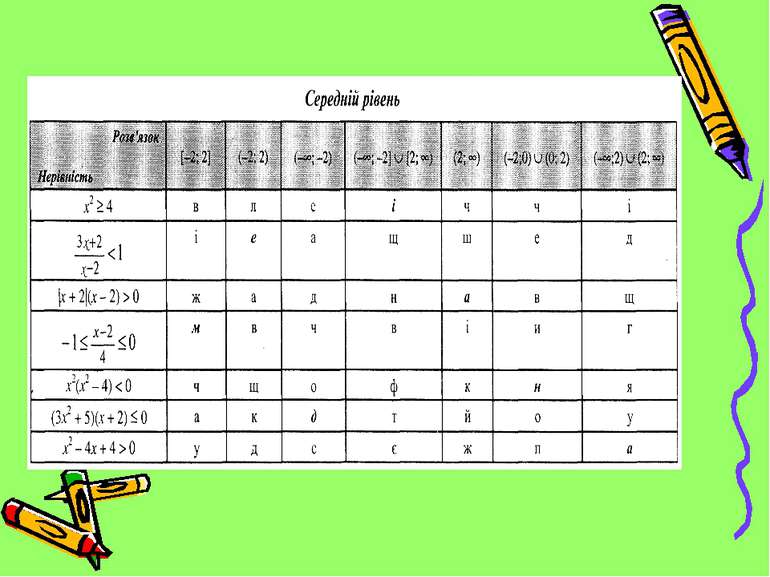
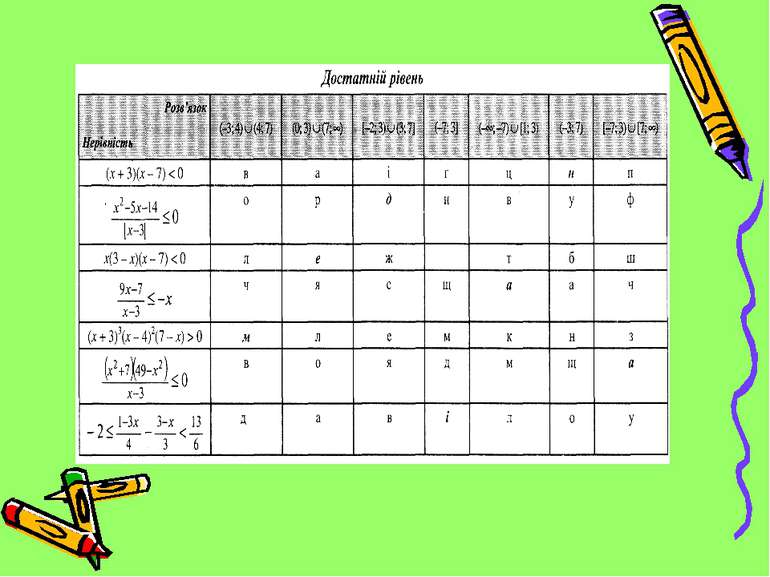
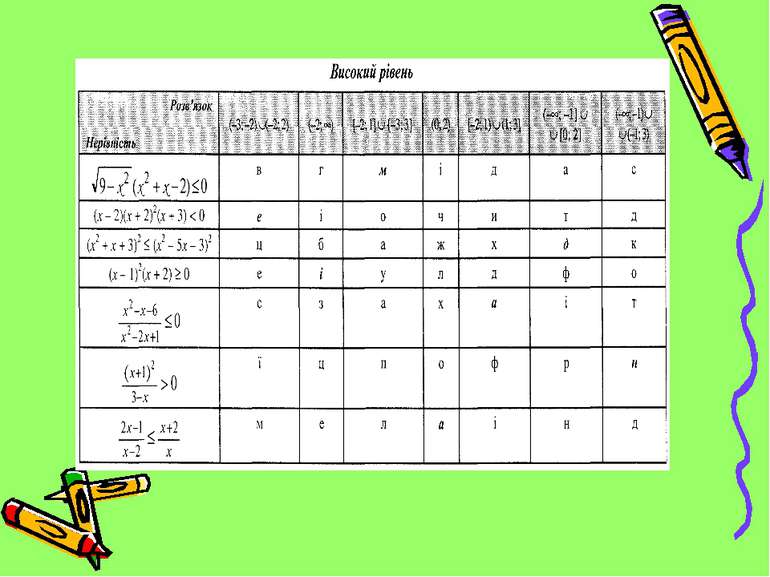
Назвіть поняття, яке: у геометрії – будучи проведеним у трикутнику, ділить його на дві рівновеликі частини; у статистиці – є характеристикою центра розподілу статистичного ряду. Цей термін можна відгадати, записавши слово, яке складається з літер, що розташовані на перетині рядка нерівності і стовпчика, до якого належить отримана відповідь (учням роздаються підготовлені картки із завданнями трьох рівнів).

Завдання №1 Знайдіть найбільший цілий розв’язок нерівності Завдання №2 Знайдіть найменше натуральне число , яке не є розв’язком нерівності Завдання №3 Скільки натуральних чисел є розв’язками нерівності < 0 VІІ. “Майстер-клас” по розв’язуванню нерівностей

VІІІ. „ Прояви творчість і ти – здоровий ! ” Користуючись рисунком складіть нерівність і запишіть її в зошит.

ІХ. Висновки Читатель! Вникни в издаваемое! Твой доброжелатель. Козьма Прутков

На завершення обговоримо основні джерела помилок. Умовно помилки можна розбити натри групи: арифметичні помилки при обчисленнях; помилки, пов’язані з незнанням чи неправильним використанням формул; помилки, що допускаються через незнання алгоритмів розв’язування Для боротьби з обчислювальними помилками не зловживайте обчисленнями „в умі” і не поспішайте „покінчити” із завданням. Пригадайте приказку: „Якщо ти виконував справу швидко, але погано, то всі забудуть, що ти робив її швидко, але будуть пам’ятати, що ти зробив її погано. Якщо ти робиш справу повільно, але добре, то всі забудуть, що ти робив її повільно, але пам’ятатимуть, що ти зробив її добре.” Незнання формул, невміння вибрати із ті, які допомагають раціонально розв’язати завдання, ускладнюють перетворення і збільшують ймовірність появи обчислювальних помилок, та ще й до того витрачається багато дорогоцінного часу. Незнання алгоритмів розв’язування нерівностей, наприклад методу інтервалів для розв’язування раціональних нерівностей чи нерівностей, що містять модулі робить завдання громіздким, а під час і неможливим. Звичайно, на контрольній чи ДПА, чи ЗНО не останню роль зіграють везіння та успіх, але пам’ятайте: „удача сопутствует упорным!”