Презентація на тему:
Найбільше і найменше значення функції на відрізку

«Просто передати знання людині неможливо. Оволодіти ними людина може шляхом власної діяльності. « Наповнити» розум не можна, він сам повинен усе засвоїть.» А.Дістеверг

Приватні підприємства ПП “Легенда” ПП “Ботанік” ПП “Функція”

Знайти область визначення функції а) у =   б) у =   в) у= D(y) = R D(y) = R/-2;2 D(y) = [2;+∞)

Знайти похідну функції а) у = б) у = в) y = г) y=

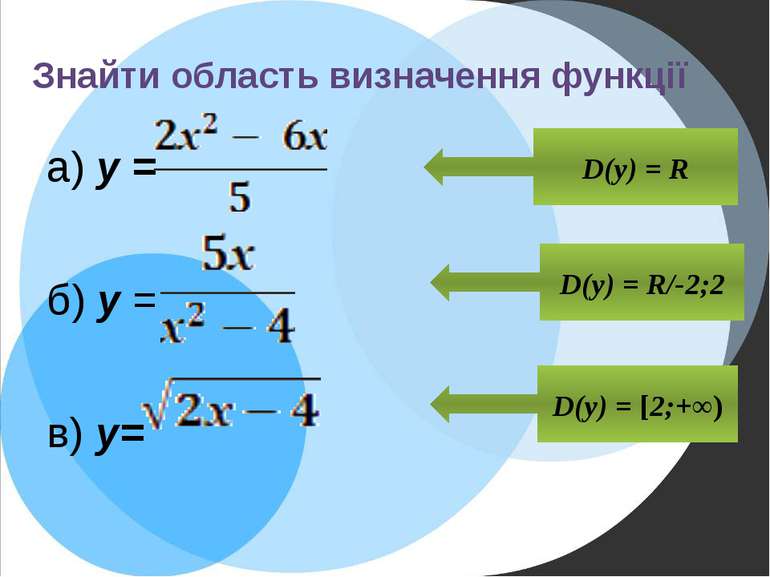
Знайти критичні точки функції а) y = Розв'язання: D(y)=R y =10x – 20 y =0, 10x – 20 =0 10x=20 x=2 Відповідь: 2. б) у = D(y)=R y =x³ – 4х y =0, x³ – 4х =0 х(х²-4)=0 х(х – 2)(х + 2) =0 x₁=0 ; х₂= 2; х₃=-2 Відповідь: -2; 0; 2. Розв'язання:

Тема уроку Найбільше і найменше значення функції на відрізку

x₁ max f(x) =f(х₀) [a;b] min f(x)= f(х₁) [a;b] y x b a x0 y=f(x)

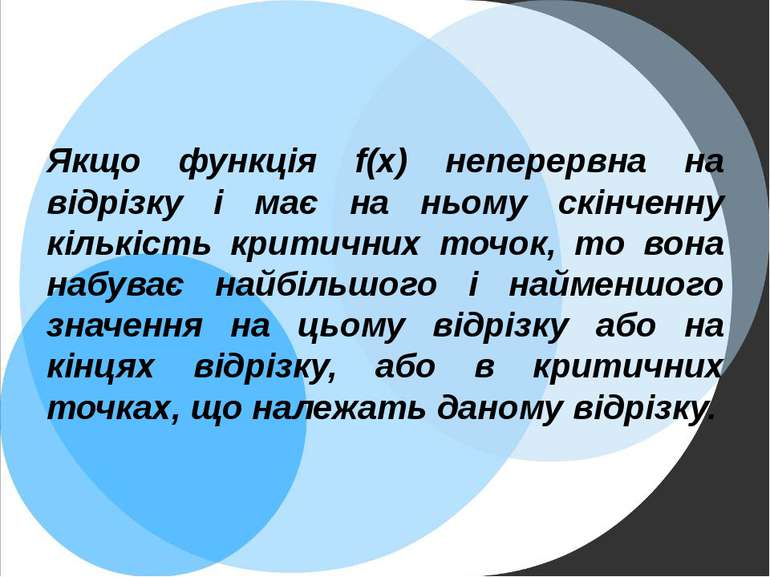
Якщо функція f(x) неперервна на відрізку і має на ньому скінченну кількість критичних точок, то вона набуває найбільшого і найменшого значення на цьому відрізку або на кінцях відрізку, або в критичних точках, що належать даному відрізку.

Знайти найбільше і найменше значення функції f(x) на вказаному відрізку, якщо f(x)=3х4- 6х2 +1, [0;2] Розв’язання: D(f)=R [0;2] Є D(f) f (x)=12x3 -12x f (x)=0, 12x(x2 – 1)=0 12x(x-1)(x+1)=0 x=0; x=1; x=-1 5. 0 є [0;2], 1 є [0;2], -1 ¢ [0;2] 6. f(0)=1 f(1)=-2 f(2)=3·16 - 6·4+1= 48 – 24 + 1=25 7. max f(x)= f(2)=25 [0;2] min f(x)= f(1)=-2 [0;2]

Алгоритм знаходження найбільшого і найменшого значення функцій на відрізку 1) Знайти область визначення функції D(f). 2) Визначити чи належить заданий відрізок D(f). 3) Знайти похідну функції f (x). 4) Знайти критичні точки функції, розв’язавши рівняння f (x)=0. 5) Визначити, які з критичних точок належать даному проміжку. 6) Знайти значення функції на кінцях проміжку та в критичних точках, що належать даному проміжку. 7) Вибрати з одержаних значень найбільше і найменше. Записати відповідь.

Фізкультхвилинка

Знайти найбільше і найменше значення функції f(x) на даному проміжку ПП “Легенда” f(x)=х4- 2х2 +5, [0;2]

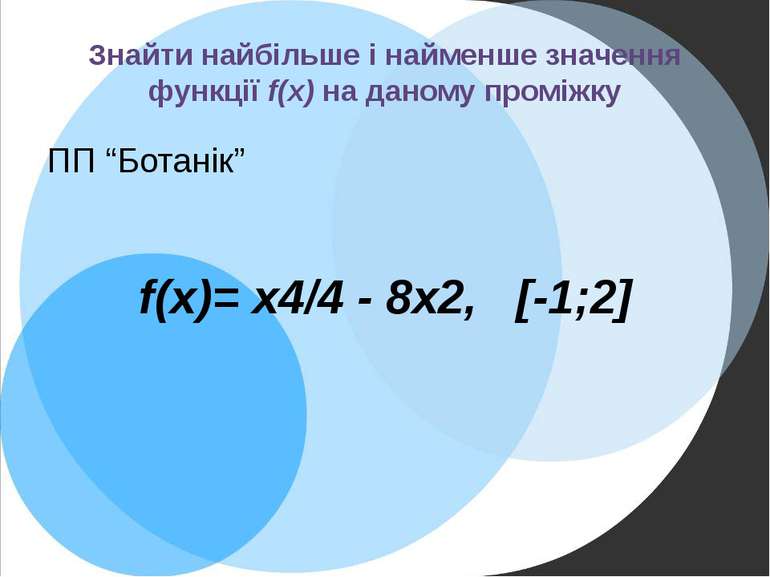
Знайти найбільше і найменше значення функції f(x) на даному проміжку ПП “Ботанік” f(x)= х4/4 - 8х2, [-1;2]

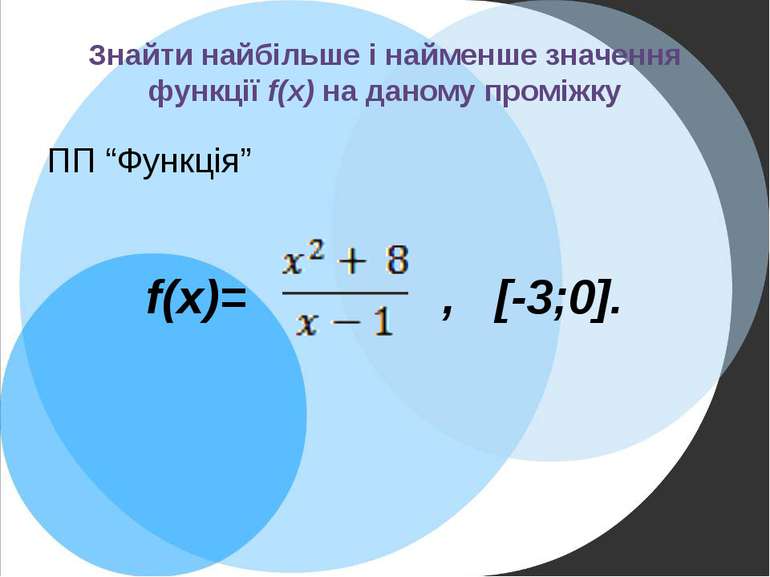
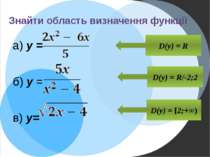
Знайти найбільше і найменше значення функції f(x) на даному проміжку ПП “Функція” f(x)= , [-3;0].

Назва ПП Функція Відрізок Найбільше значення Найменше значення «Легенда» f(x)=2х +5 [-1;1] «Ботанік» f(x)=(1/2)х [-1;0] «Функція» f(x)=х2 [-2;2] Назва ПП Функція Відрізок Найбільше значення Найменше значення «Легенда» f(x)=2х +5 [-1;1] «Ботанік» f(x)=(1/2)х [-1;0] «Функція» f(x)=х2 [-2;2]

Домашнє завдання §1, п. 13 виконати №13.6(1), №13.2, №13.4 (с.127)

Дякую за роботу на уроці!