Презентація на тему:
Математичне ралі

Рівняння виду ax2+bx+c=0 називається … Дискримінант знаходиться за формулою D= … 3. Якщо D > 0, то квадратне рівняння має … 4. Якщо D =0, то рівняння має … 5. Якщо D

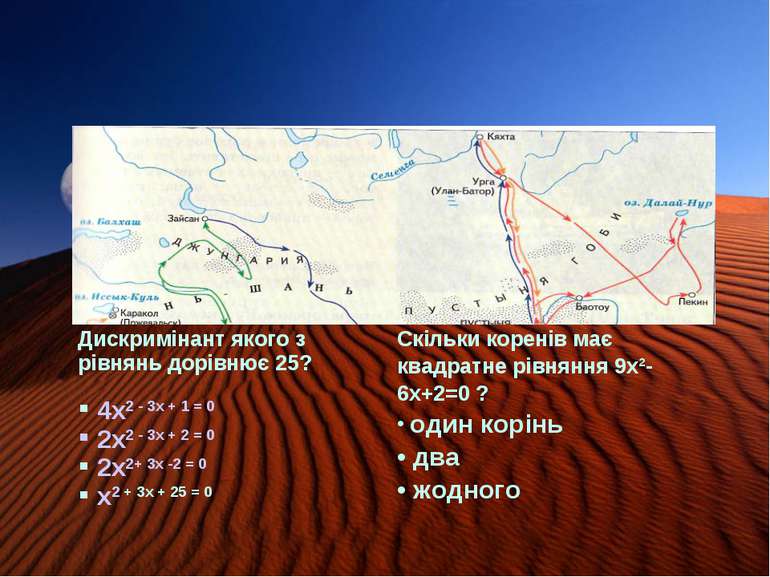
Знайти корені рівняння х²+ 36=0 6; -6 розв’язків немає -6 Розв’язати рівняння: 17х = 10х2 0; 1,7 1,7 коренів немає 0, -1,7 Дискримінант якого з рівнянь дорівнює 25? 4х2 - 3х + 1 = 0 2х2 - 3х + 2 = 0 2х2+ 3х -2 = 0 х2 + 3х + 25 = 0 Яя Скільки коренів має квадратне рівняння 9х²-6х+2=0 ? один корінь два жодного

Найти корни уравнения х²+ 36=0 6; -6 нет решений -6 Розв’яжіть рівняння: 17х = 10х2 0; 1,7 1,7 коренів немає 0, -1,7 Дискримінант якого з рівнянь дорівнює 25? 4х2 - 3х + 1 = 0 2х2 - 3х + 2 = 0 2х2+ 3х -2 = 0 х2 + 3х + 25 = 0 Скільки коренів має квадратне рівняння 9х²-6х+2=0 ? один корінь два жодного

Найти корни уравнения х²+ 36=0 6; -6 нет решений -6 Решите уравнение: 17х = 10х2 0; 1,7 1,7 нет корней 0, -1,7 Дискримінант якого з рівнянь дорівнює 25? 4х2 - 3х + 1 = 0 2х2 - 3х + 2 = 0 2х2+ 3х -2 = 0 х2 + 3х + 25 = 0 Скільки коренів має квадратне рівняння 9х²-6х+2=0 ? один корінь два жодного

Найти корни уравнения х²+ 36=0 6; -6 нет решений -6 Решите уравнение: 17х = 10х2 0; 1,7 1,7 нет корней 0, -1,7 Дискриминант какого из уравнений равен 25? 4х2 - 3х + 1 = 0 2х2 - 3х + 2 = 0 2х2+ 3х -2 = 0 х2 + 3х + 25 = 0 Скільки коренів має квадратне рівняння 9х²-6х+2=0 ? один корінь два жодного

Найти корни уравнения х²+ 36=0 6; -6 нет решений -6 Решите уравнение: 17х = 10х2 0; 1,7 1,7 нет корней 0, -1,7 Дискриминант какого из уравнений равен 25? 4х2 - 3х + 1 = 0 2х2 - 3х + 2 = 0 2х2+ 3х -2 = 0 х2 + 3х + 25 = 0 Сколько корней имеет квадратное уравнение 9х²-6х+2=0 ? один корень два ни одного

3х²-х-2=0 (х+3)*(х-4)= -12 (Х²-3х)/7+х=11 3х2 -7х +4 = 0 4х²-2х*(3х+1)=5 (х²+х)/2=(8х-7)/3

назад

назад

х²-7х+12=0 х₁+х₂=-7, х₁*х₂=12; Х₁=-4, х₂=-3 Розкласти 3х²-8х+5 на множники: 3х²-8х+5=0, х₁= 10/6= 5/3; х₂=6/6=1 3х²-8х+5= 3*( х-1)* (х-5/3)= (3х-3)*(3х-5) Знайти радіус круга, якщо його площа дорівнює 6,28 см². S=π r² 3,14* r²=6,28 r²=2 r= ±

Квадратні рівняння у Давньому Вавілоні. Необхідність вирішувати рівняння не тільки першого, але і другого ступеня ще в давнину була викликана потребою розв'язувати задачі, пов'язані з перебуванням площ земельних ділянок і з земляними роботами військового характеру, а також з розвитком астрономії і самої математики. Квадратні рівняння вміли розв'язувати близько 2000 років до нашої ери вавілоняни. Застосовуючи сучасний алгебраїчний запис, можна сказати, що в їх клинописних текстах зустрічаються, крім неповних, і повні квадратні рівняння. Правило рішення цих рівнянь, викладених у вавілонських текстах, співпадає з сучасним, проте невідомо, яким чином дійшли вавілоняни до цього правила. Майже всі знайдені досі клинописні тексти наводять тільки задачі з рішеннями, викладеними у вигляді рецептів, без вказівок щодо того, яким чином вони були знайдені. Незважаючи на високий рівень розвитку алгебри у Вавілонії, в клинописних текстах відсутні поняття від’ємного числа і загальні методи розв'язання квадратних рівнянь.

Франсуа Виет Вієт (1540-1603) зробив вирішальний крок, коли ввів символіку в усі алгебраїчні доведення шляхом використання буквених позначень для вираження як відомих, так і невідомих величин не тільки в алгебрі, а й також у тригонометрії.

= = 4х⁴-17х²+4=0 4х⁴-37х²+9=0

5x2-8x+3=0 x1=11 x2=3/5 5-8+3=0 6x2-7x+1=0 x1=11 x2=1/6 6-7+1=0 2x2+3x-5=0 x1=11 x2=5/2 2+3-5=0 x2-8x+7=0 x1=11 x2=7 1-8+7=0 Висновок : ax2+bx+c=0 a+b+c=0 x1=1, x2= с/а Розв’яжіть усно: 1) x2+23x-24=0 2) 1999x2-2000x+1=0 3) 839x2-448x-391=0

1) 4x2+7x+3=0 2) x2-9x-10=0 3) 5x2-4x-1=0 Висновок: Якщо для коефіцієнтів виконується рівність а-в+с=0, то один з коренів рівняння дорівнює -1, а другий –с/а. a-b+c=0. x1=-1; x2=- с/а Розв’зати усно: 1) 7x2+x-6=0 2) 939x2+978х+39 = 0

Молодці! Ви успішно завершили ралі. Вітаю!