Презентація на тему:
"Математичне моделювання"

Математичне моделювання Презентація учениці 9-а класу спеціалізованної школи №273 з поглибленним вивченням української мови та літератури міста Києва Данільченко Віталії

Що таке прикладна задача? У педагогічній літературі поняття прикладної задачі трактується по-різному, а саме як: • задача, що потребує перекладу з природної мови на математичну; • задача, яка близька за формулюванням і методами розв'язування до задач, що виникають на практиці; • сюжетна задача, сформульована у вигляді задачі-проблеми. Прикладна задача повинна задовольняти такі умови: 1) питання задачі формулюється так, як воно зазвичай формулюється у житті; 2) розв'язок задачі має практичну значущість; 3) дані та шукані величини задачі мають бути реальними, взятими з життя. Прикладна задача — це задача, що виникла поза математикою, але розв'язується математичними засобами. Розв’язуючи прикладну задачу, спочатку створюють її математичну модель.

Що таке математичне моделювання? Математичне моделювання – це процес побудови і вивчення математичних моделей. М.м. тією чи іншою мірою застосовують всі природничі і суспільні науки, що використовують математичний апарат для одержання спрощеного опису реальності за допомогою математичних понять. М.м. дозволяє замінити реальний об'єкт його моделлю і потім вивчати останню. Як і у разі будь-якого моделювання, математична модель не описує явище абсолютно адекватно, що залишає актуальним питання про застосовність отриманих таким шляхом даних. М.м. широко застосовується у гірництві, геології, для вивчення і аналізу процесів переробки корисних копалин.

Що таке модель? Модель- це спеціально створений об’єкт, який відображає властивості досліджуваного об’єкта. Автомобіль, літак, гребля- приклади фізичних моделей.

Основні етапи створення моделей Основні етапи створення моделей: - аналіз мети та особливостей об'єкту моделювання та формулювання на цій основі мети моделювання та вимог до моделі; - вибір критеріїв оцінювання ефективності та оптимізації; - обгрунтування класу моделі, що буде створюватись; - синтез феноменологічної моделі; - ідентифікація параметрів моделі; - перевірка відповідності синтезованої моделі вихідним вимогам та при необхідності повторення всіх або деяких етапів. При створенні моделей необхідно ураховувати, що: - спрощення моделі повинно мати межу, бо у випадку великої розбіжності між моделлю та оригіналом модель може дати помилковий матеріал; - необхідно точно знати й зафіксувати ступінь подібності суттєвих ознак між моделлю та оригіналом; - повинна бути встановлена значимість цих ознак з точки зору завдань дослідження

Класифікація моделей Формальна класифікація моделей ґрунтується на класифікації використовуваних математичних засобів. Часто будується у формі дихотомій. Наприклад, один з популярних наборів дихотомій:   Лінійні або нелінійні моделі;   Зосереджені або розподілені системи; Детерміновані або стохастичні; Статичні або динамічні; Дискретні або безперервні. і так далі. Кожна побудована модель є лінійною або нелінійною, детермінованою або стохастичною, ... Природно, що можливі і змішані типи: в одному відношенні зосереджені (за частиною параметрів), в іншому - розподілені моделі і т. д.

Що таке математична модель? Математична модель - це математичне уявлення реальності. Основна мета моделювання - дослідити ці об'єкти і передбачити результати майбутніх спостережень. Однак моделювання - це ще й метод пізнання навколишнього світу, що дає можливість керувати ним. Математична модель має важливе значення для таких наук, як: економіка, екологія, соціологія, фізика, хімія, механіка, інформатика, біологія, та ін.

Основні етапи математичного моделювання 1) Побудова моделі. На цьому етапі задається деякий «нематематичних» об'єкт - явище природи, конструкція, економічний план, виробничий процес і т. д. При цьому, як правило, чітке опис ситуації утруднено. Спочатку виявляються основні особливості явища і зв'язки між ними на якісному рівні. Потім знайдені якісні залежності формулюються мовою математики, тобто будується математична модель. Це найважча стадія моделювання. 2) Рішення математичної задачі, до якої призводить модель. На цьому етапі велика увага приділяється розробці алгоритмів і чисельних методів розв'язання задачі на ЕОМ, за допомогою яких результат може бути знайдений з необхідною точністю і за припустимий час. 3) Інтерпретація отриманих наслідків з математичної моделі. Наслідки, виведені з моделі на мові математики, інтерпретуються мовою, прийнятою в даній області. 4) Перевірка адекватності моделі. На цьому етапі з'ясовується, чи узгоджуються результати експерименту з теоретичними наслідками з моделі в межах певної точності. 5) Модифікація моделі. На цьому етапі відбувається або ускладнення моделі, щоб вона була більш адекватною дійсності, або її спрощення заради досягнення практично прийнятного рішення.

Розв’язуванням прикладної задачі математичними методами здійснюється в три етапи: 1) створення математичної моделі даної задачі; 2) розв’язування відповідної математичної задачі; 3) аналіз відповіді.

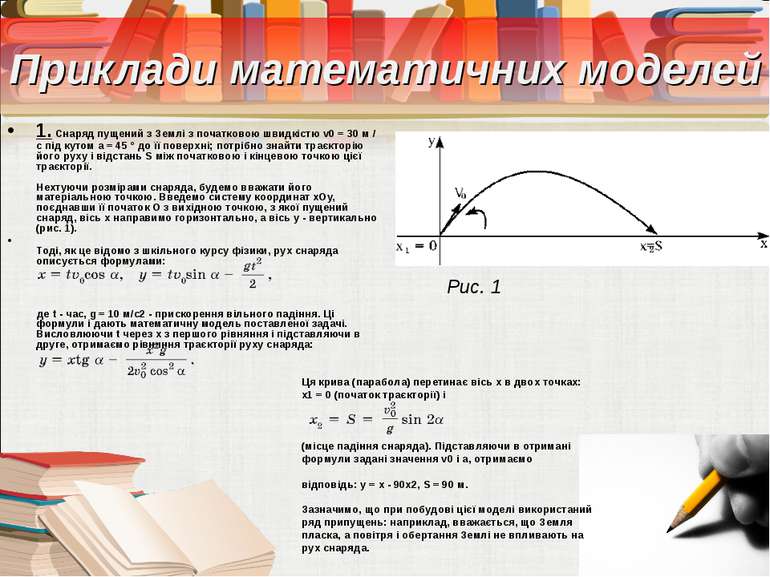
Приклади математичних моделей 1. Снаряд пущений з Землі з початковою швидкістю v0 = 30 м / с під кутом a = 45 ° до її поверхні; потрібно знайти траєкторію його руху і відстань S між початковою і кінцевою точкою цієї траєкторії. Нехтуючи розмірами снаряда, будемо вважати його матеріальною точкою. Введемо систему координат xOy, поєднавши її початок O з вихідною точкою, з якої пущений снаряд, вісь x направимо горизонтально, а вісь y - вертикально (рис. 1). Тоді, як це відомо з шкільного курсу фізики, рух снаряда описується формулами: де t - час, g = 10 м/с2 - прискорення вільного падіння. Ці формули і дають математичну модель поставленої задачі. Висловлюючи t через x з першого рівняння і підставляючи в друге, отримаємо рівняння траєкторії руху снаряда: Рис. 1 Ця крива (парабола) перетинає вісь x в двох точках: x1 = 0 (початок траєкторії) і (місце падіння снаряда). Підставляючи в отримані формули задані значення v0 і a, отримаємо відповідь: y = x - 90x2, S = 90 м. Зазначимо, що при побудові цієї моделі використаний ряд припущень: наприклад, вважається, що Земля пласка, а повітря і обертання Землі не впливають на рух снаряда.

2. Нехай N (0) - вихідне кількість атомів радіоактивної речовини, а N (t) - кількість атомів, що не розпались в момент часу t. Експериментально встановлено, що швидкість зміни кількості цих атомів N '(t) пропорційна N (t), тобто N' (t) =-lN (t), l> 0 - константа радіоактивності даної речовини. У шкільному курсі математичного аналізу показано, що вирішення цього диференціального рівняння має вигляд N (t) = N (0) e-lt. Час T, за яке число вихідних атомів зменшилася вдвічі, називається періодом напіврозпаду, і є важливою характеристикою радіоактивності речовини. Для визначення T треба покласти у формулі Тоді Наприклад, для радону l = 2,084 · 10-6, і отже, T = 3,15 сут.