Презентація на тему:
Рiвняння сфери,прямої, площини

Рiвняння сфери,прямої, площини

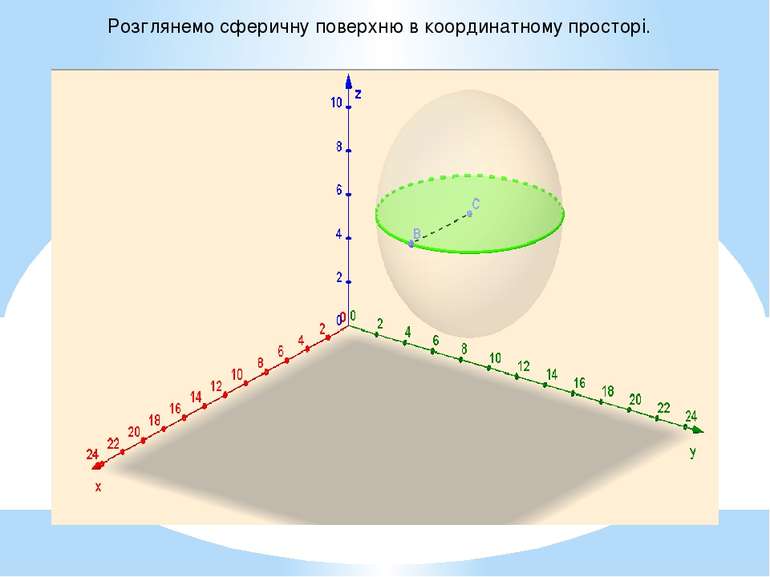
Рiвняння сфери Сферою називається геометричне місце точок простору, рівновід-далений від заданої точки-центра сфери. Якщо центр сфери є точка С(a; b; c), а радіус R, тоді рівняння сфери буде: (x – a)2 + (y – b)2 + (z – c)2 = R2.     (2.43) Якщо центр сфери знаходиться в початку координат О(0; 0; 0) і радіус є R, тоді рівняння сфери буде: x2 + y2 + z2 = R2. Рівняння кулі легко записати, якщо її розглядати як множину точок, віддалену від деякої точки С на відстань, що не перевищує  R. Отже, точки з координатами   ( х,у,z ),що задовольняють нерівність , утворюють кулю.

Розглянемо сферичну поверхню в координатному просторі.   

Рівняння прямої Пряма (пряма лінія) - це нескінченна лінія, по якій проходить найкоротший шлях між будь-якими двома її точками. Рівняння прямої на площині Будь-яку пряму на площині можна задати рівнянням прямої першого ступеня вигляду A x+ By+ C= 0. Де A і B не можуть одночасно дорівнювати нулю. Рівняння прямої з кутовим коефіцієнтом Загальне рівняння прямої коли B≠0 можна привести к вигляду y= kx+ b,де k- кутовий коефіцієнт, який дорівнює тангенсу кута, утвореного даною прямою і додатним напрямком осі ОХ

Рівняння прямої в відрізках на осях Якщо пряма перетинає вісі OX і OY в точках з координатами (a, 0) і (0, b), то вона може бути знайдена, якщо використати формулу рівняння прямої в відрізках Рівняння прямої, що проходить через дві різні точки на площині Якщо пряма проходить через дві точки A(x1, y1) і B(x2, y2), такі що x1 ≠ x2 і y1 ≠ y2 то рівняння прямої можна знайти, використовуючи наступну формулу x  +  y  =1 a b x- x1  =  y- y1 x2-x1 y2-y1

Параметричне рівняння прямої на площині Параметричне рівняння прямої може бути записане наступним чином де (x0, y0) - координати точки, що лежить на прямій, {l, m}- координати напрямного вектора прямої. Канонічне рівняння прямої на площині Якщо відомі координати точки A(x0, y0), що лежить на прямій і напрямного вектора n= {l; m}, то рівняння прямої можна записати в канонічному вигляді, використовуючи наступну формулу x=lt+ x0 y= mt+y0 x- x0  =  y- y0 l m

Рівняння прямої в просторі Рівняння прямої, що проходить через дві різні точки в просторі Якщо пряма, що проходить через дві точки A(x1, y1, z1) і B(x2, y2, z2), такі що x1 ≠ x2, y1 ≠ y2 і z1 ≠ z2 то рівняння прямої можна знайти, якщо використати наступну формулу x- x1  =  y- y1  =  z- z1 x2-x1 y2-y1 z2-z1

Параметричне рівняння прямої в просторі Параметричне рівняння прямої може бути записане наступним чином де (x0, y0, z0) - координати точки, що лежить на прямій, {l; m; n}- координати напрямного вектора прямої. Канонічне рівняння прямої в просторі Якщо відомі координати точки A(x0, y0, z0), що лежить на прямій і напрямного вектора n= {l; m; n}, то рівняння прямої можна записати у каноничному вигляді, якщо використати наступну формулу x=lt+ x0 y=mt+ y0 z= nt+ z0 x- x0  =  y- y0  =  z- z0 l m n

Пряма як лінія перетину двох площин Якщо пряма є перетином двох плщин, то її рівняння можна задати наступною системою рівнянь за умови, що не має місце рівність A1x+ B1y+ C1z+D1= 0 A2x+ B2y+ C2z+D2= 0 A1  =  B1  =  C1 . A2 B2 C2

Рівняння площини. Площина - це поверхня, яка повністю містить, кожну пряму, що з'єднує будь-які її точки. Загальне рівняння площини Будь-яку площину можна задати рівнянням площини першого ступеня вигляду Ax+ By+ Cz+ D= 0, де A, B і C не можуть одночасно дорівнювати нулю. Рівняння площини в відрізках Якщо площина перетинає осі OX, OY і OZ в точках з координатами (a,0,0),(0,b,0) і (0,0,с), то вона може бути знайдена, якщо використати формулу рівняння площини в відрізках x  +  y  +  z  = 1 a b c

Рівняння площини, що проходить через точку, перпендикулярно вектору нормалі Щоб скласти рівняння площини, за координатами точки площини M(x0, y0, z0) і вектора нормалі площини n= {A; B; C} можна використати наступну формулу. A(x - x0) + B(y - y0) + C(z - z0) = 0 Рівняння площини, що проходить через три задані точки, які не лежать на одній прямій Якщо задані координати трьох точок A(x1, y1, z1), B(x2, y2, z2) і C(x3, y3, z3), які лежать на площині, то рівняння площини можна знайти за наступною формулою