Презентація на тему:
Точка і пряма. Рівняння прямої. Коло

Обчислювальна геометрія Тема “Точка і пряма. Рівняння прямої. Коло” Профільна інформатика Лінія “АТП”

Точка і пряма Точка на площині задається двома координатами (х; у), де перший параметр - положення точки відносно осі абсцис Ох, а другий - відносно осі ординат Оу. Обидва параметри задаються цілими або дійсними числами. Як відомо з математики, пряму на площині можна задати у вигляді загального рівняння: ах + by + с = 0.

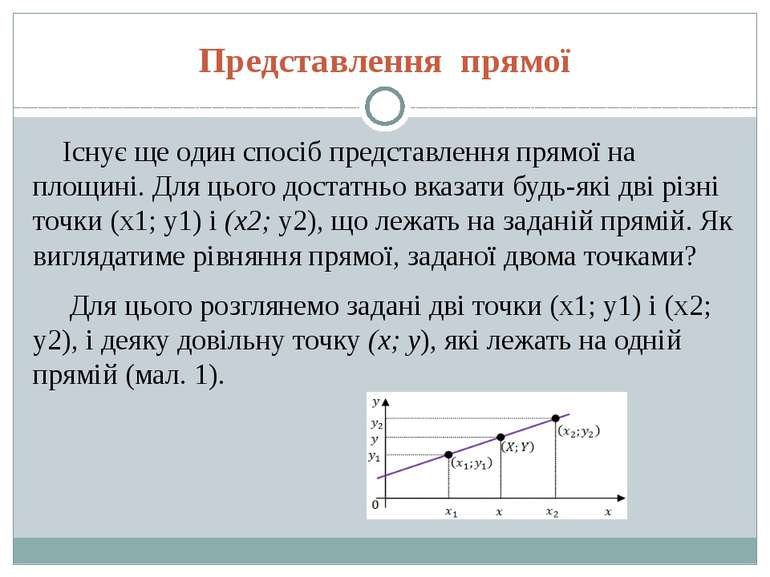
Представлення прямої Існує ще один спосіб представлення прямої на площині. Для цього достатньо вказати будь-які дві різні точки (x1; y1) і (х2; y2), що лежать на заданій прямій. Як виглядатиме рівняння прямої, заданої двома точками? Для цього розглянемо задані дві точки (x1; y1) і (х2; y2), і деяку довільну точку (x; y), які лежать на одній прямій (мал. 1).

Рівняння прямої Відповідно до умови подібності можна записати таке відношення: . Отримане рівняння прямої, що проходить через 2 дані точки. Кутовий коефіцієнт цієї прямої: . Рівняння прямої, що проходить через дві задані точки, краще розглядати у такому вигляді:

Представлення коефіцієнтів рівняння прямої через координати точок Розглянемо питання представлення коефіцієнтів a, b, c через координати двох точок (x1; y1) і (х2; y2), розміщених на прямій, яка проходить через них. Це буде корисним для проведення аналізу взаємного розташування заданих точок і прямих, де необхідно буде мати справу з коефіцієнтами загальних рівнянь прямих . Звівши подібні члени в наведеному вище рівнянні, отримаємо:

Визначення належності точки даній прямій Для визначення чи розміщені три дані точки (x1; y1), (х2; y2) і (x3; y3) на одній прямій скористаємося рівнянням прямої: , проте, щоб досягнути точності результату краще скористатися рівнянням у такому вигляді:

Розглянемо часткові випадки: 1) Якщо С=0, рівняння матиме вигляд: і визначатиме пряму, що проходить через початок координат; 2) Якщо В=0 ( ), рівняння матиме вигляд або і визначає пряму, паралельну осі OY, якщо крім цього ще й С=0, отримаємо рівняння осі OY: ; 3) Якщо А=0 ( ), рівняння матиме вигляд , або і визначає пряму, паралельну осі OX. Якщо крім цього С=0, то отримуємо рівняння осі OX: .

Кут між прямими Для визначення кута між двома прямими і , скористаємося формулою: . Кут визначається від першої прямої до другої проти годинникової стрілки.

Ділення відрізка в заданому відношенні Якщо задані точки, що є кінцями відрізка і , та відомо, що точка належить відрізку , то відрізок ділиться цією точкою у відношенні : , тоді координати точки М визначаються за формулами: або . Частковим випадком є середина відрізка: , .

Взаємне розміщення двох точок Про взаємне розміщення двох точок (x1; y1) і (х2; y2) можна говорити для таких випадків: 1). Якщо і , то задані точки знаходяться на одній вертикалі на площині; 2). Якщо і , то задані точки знаходяться на одній горизонталі на площині; 3). Якщо і , то задані точки збігаються; 4). Якщо і , то задані точки не збігаються на площині й не знаходяться на одній горизонталі або вертикалі.

Взаємне розміщення двох прямих Розглянемо, чи перетинаються ці прямі, чи вони паралельні, чи обидва ці рівняння представляють одну і ту саму пряму. Знаючи коефіцієнти загальних рівнянь типу двох заданих прямих (а1, b1, с1) та (а2, b2, с2), можна дати відповідь на всі поставлені запитання. 1). Якщо , , , то це означає, що обидва рівняння описують одну і ту саму пряму. 2). Якщо , або то це свідчить про те, що задані прямі паралельні.

До уваги Оскільки при діленні дійсних чисел можна втратити правильну відповідь на точності отриманих результатів, то краще перевірити одночасне виконання таких умов: ; ; .

Визначення точки перетину прямих Якщо умови збігу та паралельності заданих двох прямих не виконуються, то можна стверджувати, що вони перетинаються. А в цьому разі може виникнути необхідність визначення координат точки перетину таких прямих. Їх можна знайти, розв'язавши систему лінійних рівнянь: На першому кроці з першого рівняння визначимо змінну х через у: Підставимо отриманий вираз у друге рівняння, визначивши значення у через коефіцієнти (а1, b1, с1) та (а2, b2, с2) двох заданих рівнянь прямих: . Отриманий вираз для у дасть змогу вивести аналогічний вираз для х: .

Перпендикулярність прямих Для визначення перпендикулярності двох прямих можна скористатися перевіркою умов: або

Взаємне розміщення точок і прямої Нехай задана пряма загальним рівнянням ах + by + с = 0 та дві точки (x1;y1) і (х2;y2). Ознакою того, що точка (х0; у0) лежить на прямій, є ах0+bуо+с=0. Якщо точка не лежить на прямій, то зрозуміло, що . А це означає, що значення ах0 + bу0 + с або додатне, або від'ємне. Оскільки пряма ах0 + bу0 + с = 0 ділить координатну площину на дві півплощини, то виявляється, що всі точки (xi; yi), які лежать одній з них, дають однаковий знак виразу ах0 + bу0 + с. Отже, якщо для двох заданих точок (x1; y1) і (х2; y2) має місце вираз (ах1 + bу1 + с)(ах2 + bу2 + с)>0, то це означатиме, що ці дві точки лежать по один бік від заданої прямої ах + by+с=0, а якщо (ах1 + bу1 + с)(ах2 + bу2 + с)< 0, то по різні.

Рівняння кола. Взаємне розміщення точки і кола Коло — геометричне місце точок площини, відстань від яких до заданої точки, що називається центром кола, є постійною величиною і дорівнює радіусу кола. Коло на площині, даного радіуса R, у певній вибраній декартовій системі координат XOY і , з центром в точці описується стандартним рівнянням: , або загальним рівнянням: де , , . Якщо центр кола знаходиться в початку координат (0, 0), то рівняння спрощується до такого вигляду: . Нехай Р( ) – точка кола, тоді рівняння дотичної до кола в даній точці має вигляд: , або